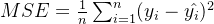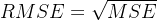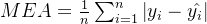🌻个人主页：相洋同学

🥇学习在于行动、总结和坚持，共勉！

目录

1.均方误差 (MSE - Mean Squared Error)

2.均方误差根（RMSE-Root Mean Squared Error）

3.平均绝对误差（MEA-Mean Absolute Error）

4.决定系数（-Coefficient of Determination）

5.代码演示

#学习总结#
模型训练好之后，对其进行评价是十分必要的。对于回归模型的性能评价，主要是通过衡量模型预测值与实际值之间的差异来实现的。

主要的评价方式有如下几种：

1.均方误差 (MSE - Mean Squared Error)

• 计算公式为：
•  其中，是观测值，是模型预测值。
• MSE衡量的是预测值与实际值差异的平方和的均值，越小表示模型越好。

2.均方误差根（RMSE-Root Mean Squared Error）

• 计算公式为：
• RMSE是MSE的平方根，对于较大的误差会给予更大的惩罚，单位与原数据保持一致，便于理解

3.平均绝对误差（MEA-Mean Absolute Error）

• 计算公式为：
• MAE 衡量的是预测值与实际值差异的绝对值的平均值，对所有的差异给予相等权重。

4.决定系数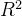（-Coefficient of Determination）

• 计算公式为：
• 其中，是观测值的平均值
• 表示模型能够解释的数据变异性的比例，越接近1，模型的解释能力越强。

决定系数是常用的观测指标，根据公式我们不难得到以下结论

1. 当=0或接近0时，相当于取平均值的效果
2. 当<0时，代表模型效果较差，还不如取平均值的效果，理论上取值可以无穷小
3. 当>0，接近1代表模型效果较好

5.代码演示

代码示例：

#导入相应的方法
from sklearn.metrics import mean_squared_error, mean_absolute_error, r2_score
print("均方误差(MSE)：", mean_squared_error(y_test, y_hat))
print("根均方误差(RMSE)：", np.sqrt(mean_squared_error(y_test, y_hat)))
print("平均绝对值误差(MAE)：", mean_absolute_error(y_test, y_hat))
print("训练集R^2：", r2_score(y_train, lr.predict(X_train)))
print("测试集R^2：", r2_score(y_test, y_hat))
# socre求解的就是r^2的值。但是r2_score方法与score方法传递参数的内容是不同的。
print("训练集R^2：", lr.score(X_train, y_train))
print("测试集R^2：", lr.score(X_test, y_test))

输出：

均方误差(MSE)： 3.691394845698606
根均方误差(RMSE)： 1.921300300759516
平均绝对值误差(MAE)： 1.2333759522850203
训练集R^2： 0.9065727532450596
测试集R^2： 0.8649018906637793
训练集R^2： 0.9065727532450596
测试集R^2： 0.8649018906637793

每种指标都有其优缺点，选择哪种指标取决于具体问题和数据的特点。例如，如果数据中的异常值影响较大，可能会选择使用 MAE 或 MAPE，因为相比于 MSE，它们对异常值的敏感度较低。而 R² 和调整 R² 则更多地用于解释模型对数据的拟合程度。

以上

学习在于总结和坚持，共勉