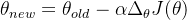🌻个人主页:相洋同学
🥇学习在于行动、总结和坚持,共勉!
目录
#学习记录#
梯度下降和反向传播是机器学习和深度学习中非常重要的两个概念,尤其是在训练神经网络时。
今天我们来总结一下
1 梯度下降(Gradient Descent)
梯度下降是一种优化算法,用来最小化(或最大化)一个函数。在机器学习中这个函数通常是损失函数(loss function),它衡量的是模型预测值与真实值之间的差距,简单来说,梯度下降就是寻找损失函数的最小值(或最小点)的过程。
1.1 极小值问题
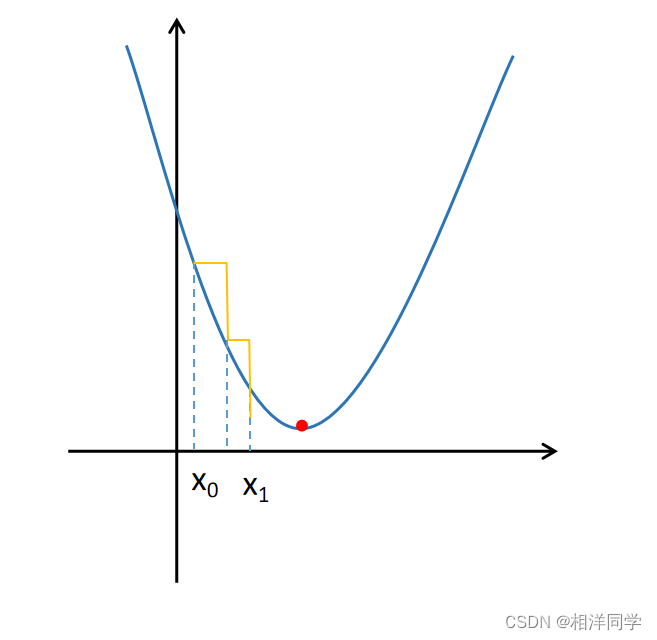
我们先来看一个找极小值问题:
函数f(x)的值受x影响
目标:找到合适的x值,使得f(x)最小
方法:
1.选取一个
2.根据导数的正负,决定
3.迭代进行1,2,直到x不在变化(或是变化极小)
1.2 梯度
所谓梯度就是指损失函数在当前点上的斜率或方向。它会告诉你损失函数增加最快的方向。意义与导数基本一致
原函数: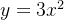
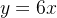
原函数: 导函数:
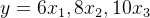
1.3 梯度下降法
- 选择初始参数:首先,随机选择一组开始的参数。
- 计算梯度:梯度指的是损失函数在当前参数下的导数,它指向损失最快增加的方向。因此,向梯度的反方向更新参数,可以使得损失减小。
- 更新参数:使用下面的公式来更新每个参数:
其中,θ 是参数,α 是学习率(控制更新的步长),J(θ) 是损失函数。
在模型训练过程中,我们肯定是希望损失函数越小越好,证明模型越好。所以模型学习的目标就是损失函数最小化,而模型权重会影响损失函数值,所以我们通过梯度下降来找到最优权重。
2 反向传播(Backpropagation)
反向传播是一种特别高效计算梯度的方法,它在神经网络中被广泛使用。当我们在神经网络中使用梯度下降时,反向传播帮助我们找到每一层参数的梯度。
2.1 完整过程
- 前向传播:输入数据在神经网络中向前传递,直到产生输出和损失。
- 计算损失:根据模型的输出和实际值计算损失函数。
- 反向传播:计算损失函数关于每个参数的梯度。这个过程从输出层开始,逆向通过网络,使用链式法则逐层计算梯度。
- 更新参数:一旦得到梯度,就使用梯度下降的方法更新网络中的参数。
Tips:方向传播之所以叫反向传播,主要就是因为要逆向通过网络使用呢链式法则逐层计算梯度。
2.2 代码演示
上代码:
import matplotlib.pyplot as pyplot
import math
import sys
# 1.构造样本,0 - 100 的 100 个点
X = [0.01 * x for x in range(100)]
# 预定义函数,y = 4x^2 + 5x + 6
Y = [4 * x ** 2 + 5 * x + 6 for x in X]
def func(x):
# 1.这里是选用的模型,线性模型
y = w1 * x ** 2 + w2 * x + w3
return y
def loss(y_pred, y_true):
# 2.损失函数,均方差 MSE mean square error
return (y_pred - y_true) ** 2
# 3.权重随机初始化,这样也可以理解为模型的初始化,预训练模型的意义就是让模型的初始化更好
w1, w2, w3 = 1, 0, 1
# 学习率设置,这里是一个超参数,需要调参(控制权重更新的幅度)
lr = 0.001
# 每次迭代中使用训练模型样本的数量,其对模型的训练效果和训练速度都有重要影响
batch_size = 1
# 训练过程
for epoch in range(1000): # 模型训练的轮数
epoch_loss = 0 # 记录每轮的损失
grad_w1 = 0
grad_w2 = 0
grad_w3 = 0
count = 0 # 这里是初始化
for x, y_true in zip(X, Y):
count += 1
y_pred = func(x)
epoch_loss += loss(y_pred, y_true)
# 梯度计算,这里是手动计算梯度,pytorch会自动计算梯度
# 梯度计算就是求导,这里是求偏导
grad_w1 += 2 * (y_pred - y_true) * x ** 2
grad_w2 += 2 * (y_pred - y_true) * x
grad_w3 += 2 * (y_pred - y_true)
# 权重更新
if count == batch_size:
w1 = w1 - lr * grad_w1/batch_size # sgd 随机梯度下降
w2 = w2 - lr * grad_w2/batch_size
w3 = w3 - lr * grad_w3/batch_size
count = 0 # 这里是每次更新
grad_w1 = 0
grad_w2 = 0
grad_w3 = 0
epoch_loss /= len(X)
print("第%d轮, loss %f" % (epoch, epoch_loss))
if epoch_loss < 0.00001:
break
print(f"训练后权重:w1:{w1} w2:{w2} w3:{w3}")
# 使用训练后模型输出预测值
Yp = [func(i) for i in X]
# 预测值与真实值比对数据分布(通过图像查看预测效果)
pyplot.scatter(X, Y, color="green")
pyplot.scatter(X, Yp)
pyplot.show()
以上代码中我们自己提前构造了一个数据集供模型进行预测。
值得注意的点
1.求导的过程我们手动完成了,在使用pytorch构建神经网络的时候,其内部会自动完成求导。
2.batch_size是每次迭代中使用训练模型样本的数量,也就是每算多少个样本更新一次梯度。举个例子来说,就像我们在学习过程中进行总结一样。我们是每天总结调整策略还是每个星期,每个小时或者每年。很显然,每个小时太浪费时间,每年的话时间又太长。
3.梯度下降的公式还有不同的,我们称其为优化器。不同优化器对训练的模型有不同影响,损失函数也是,后续学习中我们会接触更多。
以上
学习在于坚持和总结,共勉