🛺图的遍历:
注意:在遍历的过程中,可能会出现 回路 ( 已经访问过的节点还要重新访问一次 ) \color{orange}回路(已经访问过的节点还要重新访问一次) 回路(已经访问过的节点还要重新访问一次).
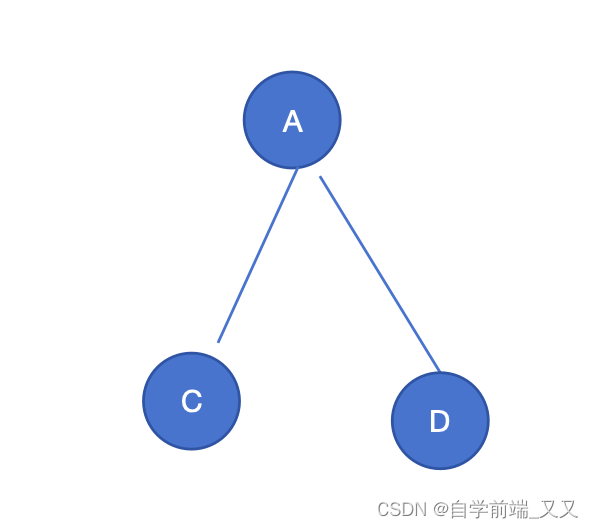
当从A开始访问时,先访问A,然后C,这时候由于C和D没有连接,无法直接到达D,需要再回到A,此时A就被多次访问了。
可以创建一个数组用于保存访问过的顶点。
🏍️深度优先搜索(Depth_First Search ——DFS)
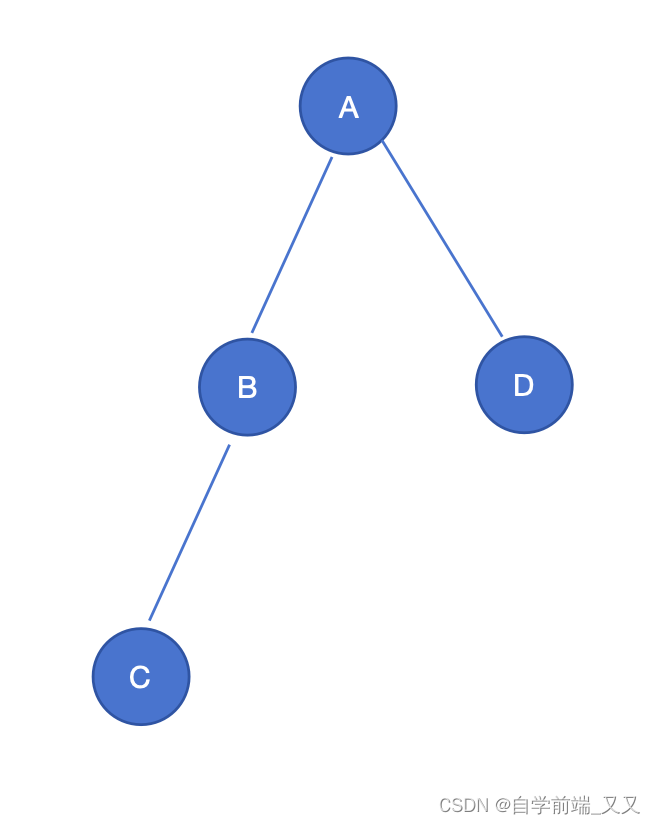
如下面的图,
先
访问
A
顶点
\color{orange}访问A顶点
访问A顶点,发现A顶点有两个边,随便选择一个,B顶点
访问
B
顶点
\color{orange}访问B顶点
访问B顶点,发现有两条边,一个与A连接,一个与C连接,而与A连接的已经访问过了,则访问C顶点。
访问
C
顶点
\color{orange}访问C顶点
访问C顶点,之后没有边了
退回
B
顶点
\color{orange}退回B顶点
退回B顶点,连接的现条边都访问过了。
$\color{orange}退回A顶点,发现与D连接的边没有访问。
访问
D
顶点
\color{orange}访问D顶点
访问D顶点,搜索结束
🛵算法效率分析
🚲连通图
邻接矩阵
\color{#5ecffd}邻接矩阵
邻接矩阵 —— 遍历图中每个顶点都要从头扫描该顶点所在行,时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)
邻接表
\color{#5ecffd}邻接表
邻接表 —— 虽然有2e个表结点,但只需要扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为
O
(
n
+
e
)
O(n+e)
O(n+e)
注:
稠密图
\color{orange}稠密图
稠密图适合在邻接矩阵上进行深度遍历。
稀疏图
\color{orange}稀疏图
稀疏图适合在邻接表上进行深度遍历。
🏍️广度优先搜索(Breadth_First Search ——BFS)
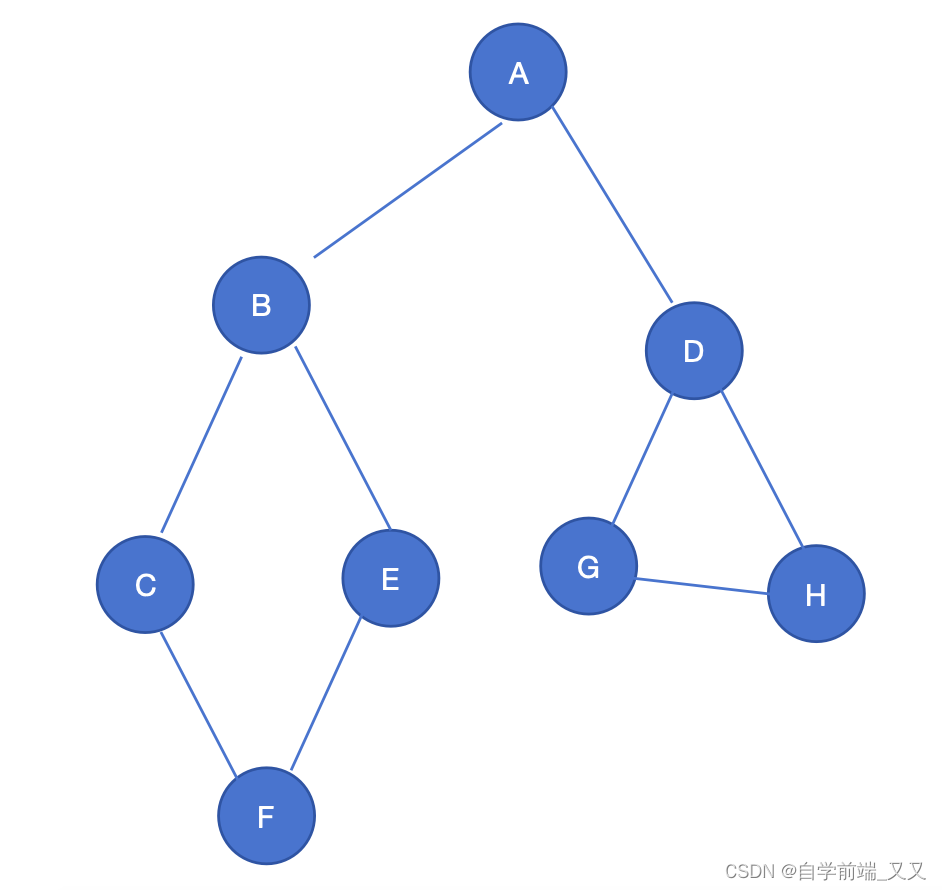
如图:
先
访问
A
顶点
\color{orange}访问A顶点
访问A顶点,发现A顶点有两个边
访问
B
、
D
顶点
\color{orange}访问B、D顶点
访问B、D顶点,发现B顶点与D顶点都有两条边没有访问。
访问
C
、
E
,
G
、
H
顶点
\color{orange}访问C、E,G、H顶点
访问C、E,G、H顶点,右边已经没有顶点要访问了,而左边还有一个
访问
F
顶点
\color{orange}访问F顶点
访问F顶点,搜索结束。
🛵算法效率分析
🚲连通图
邻接矩阵
\color{#5ecffd}邻接矩阵
邻接矩阵 —— 遍历图中每个顶点都要从头扫描该顶点所在行,时间复杂度为
O
(
n
2
)
O(n^2)
O(n2)
邻接表
\color{#5ecffd}邻接表
邻接表 —— 虽然有2e个表结点,但只需要扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为
O
(
n
+
e
)
O(n+e)
O(n+e)
DFS算法与BFS算法效率比较
空间复杂度相同,都是
O
(
n
)
O(n)
O(n)(使用了堆栈或队列)
时间复杂度与存储结构(邻接矩阵或邻接表)有关,而与搜索路径无关