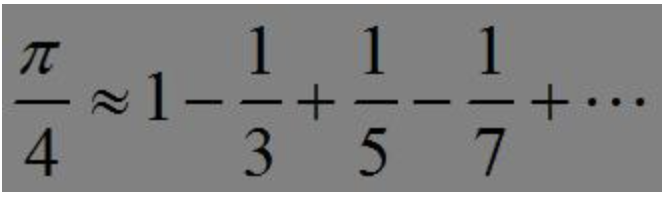题目来自：codeup，一些语法题适合初学C/C++练手，熟练代码；

例题5-1-1 连续自然数求和

题目描述：
求1+2+3+…+100，要求用while语句实现
输入
无
输出
无

#include <iostream>
using namespace std;
int main(){	
	int  n=1;
	int  i=1;
	while(i<100){
		i++;
		n += i;
	}
	cout << n << endl;
	return 0;
}

求1+2+3+…+100，要求用do while语句实现

#include <iostream>

using namespace std;

int main(){

	int  n=1;
	int  i=1;
	do{
		i++;
		n += i;
	}while(i<100);

	cout << n << endl;
	return 0;
}

求1+2+3+…+100，要求用for语句实现

#include <iostream>
using namespace std;

int main(){

	int  n=1;
	for(int i=2;i<=100; i++){
		n +=i;
	}
	cout << n << endl;
	return 0;
}

#include <iostream>

using namespace std;

int main(){

	int  n, a=1;
	cin >> n;
	for(int i=2;; i++){
		a += i;
		if(i == n) break;
	}
	cout << a << endl;
	return 0;
}

编程实现求1+2+3+…和的程序，要求得到使使和数大于1000的最小正整数。

#include <iostream>
using namespace std;

int main(){

	int  n,a=1;
	cin >> n;
	for (int i=2; ;i++){
		a += i;
		if(a >1000){
			cout << i << endl;
			break;
		}
	}
	return 0;
}

例题5-6 矩阵输出

输出以下4*5的矩阵

  1  2  3  4  5
  2  4  6  8 10
  3  6  9 12 15
  4  8 12 16 20

要求使用循环实现，注意每行输出5个数字，每个数字占3个字符的宽度，右对齐。
输入
无
输出
每行输出5个数字，每个数字占3个字符的宽度，右对齐。

#include <cstdio>

int main(){
	for (int i=1; i<=4; i++){
		for (int j=1; j<=5; j++){
			printf("%3d", i*j);
		}
		printf("\n");
	}
	return 0;
}

例题5-7 求圆周率pi的近似值

用如下公式

求圆周率PI的近似值，直到发现某一项的绝对值小于10-6为止（该项不累加）。
要求输出的结果总宽度占10位，其中小数部分为8位。
程序中使用浮点型数据时，请定义为双精度double类型。
如果需要计算绝对值，可以使用C语言数学库提供的函数fabs，如求x的绝对值，则为fabs(x).

输入

无

输出：
输出的结果总宽度占10位，其中小数部分为8位。
末尾输出换行。

PI=圆周率的近似值

#include <cstdio>
#include <cmath>

int main(){

	const double m = 1e-6;
	double PI = 1.0;

	for (double i=1; ; i++){
		double b = (1.0/(2*i+1.0)) * pow(-1.0,i);
		if(fabs(b) < m) break;
		PI += b;
	}
	printf("PI=%10.8f\n", PI*4);

	return 0;
}

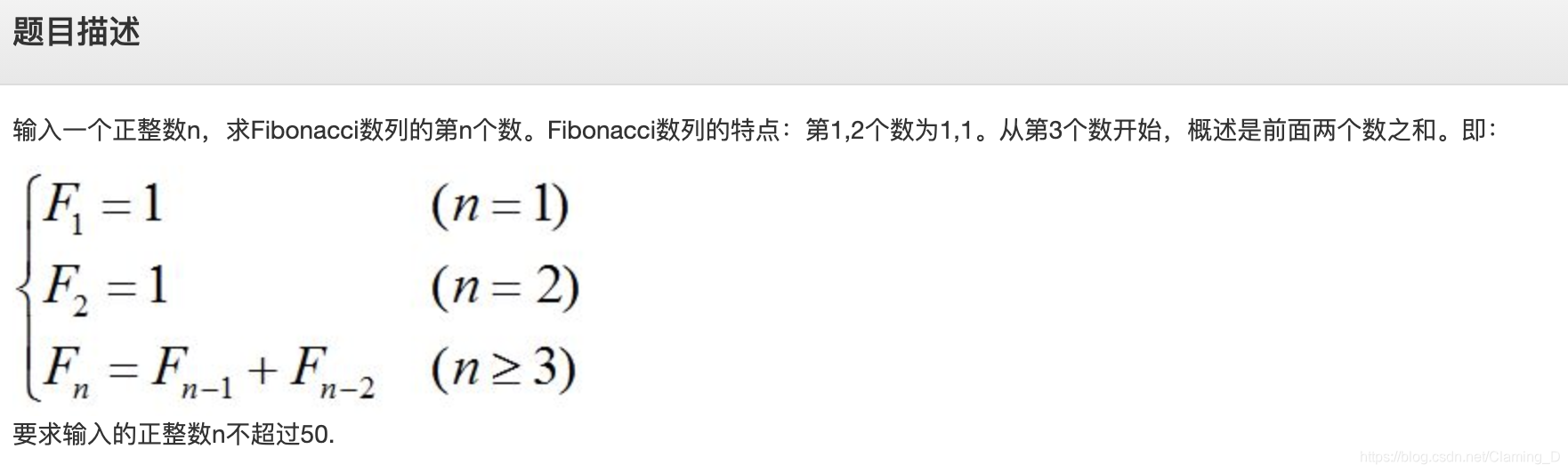
例题5-8 Fibonacci数列

输入
一个不超过50的正整数
输出
Fibonacci数列的第n个数，末尾输出换行。

#include <cstdio>

int main(){

	int n=0, ans=0, n1=1, n2=1;  //用n1表示 f(n-1) 用n2表示f(n-2)
	scanf("%d", &n);
	if(n==1 || n==2){
		printf("1\n");
		return 0;
	}
	for (int i=0; i< n-2; i++){
		
		ans = n1 + n2; // f(n) = f(n-1) + f(n-2)
		// 下一轮
		n2 = n1; // f(n-2) = f(n-1);
		n1 = ans; // f(n-1) = f(n);
		
	}
	printf("%d\n", ans);
	return 0;
}

习题5-10 分数序列求和

输入
无
输出
小数点后保留6位小数，末尾输出换行。
思路
对于两个分式$\frac{a}{b}$,$\frac{c}{d}$很容易看出$c=a+b$，$d=a$

#include <cstdio>

int main(){

	double sum=1;
	double n=1, n2=1, n3=1;
	for (int i=0; i<20; i++){
		n = n2 + n3; 
		sum += n/n2; // 相比fibonacci主要是多了这一步
		n3 = n2;
		n2 = n;
	}
	printf("%.6f\n", sum);
	return 0;
}