目录
1.归并排序的认识
归并排序的思想
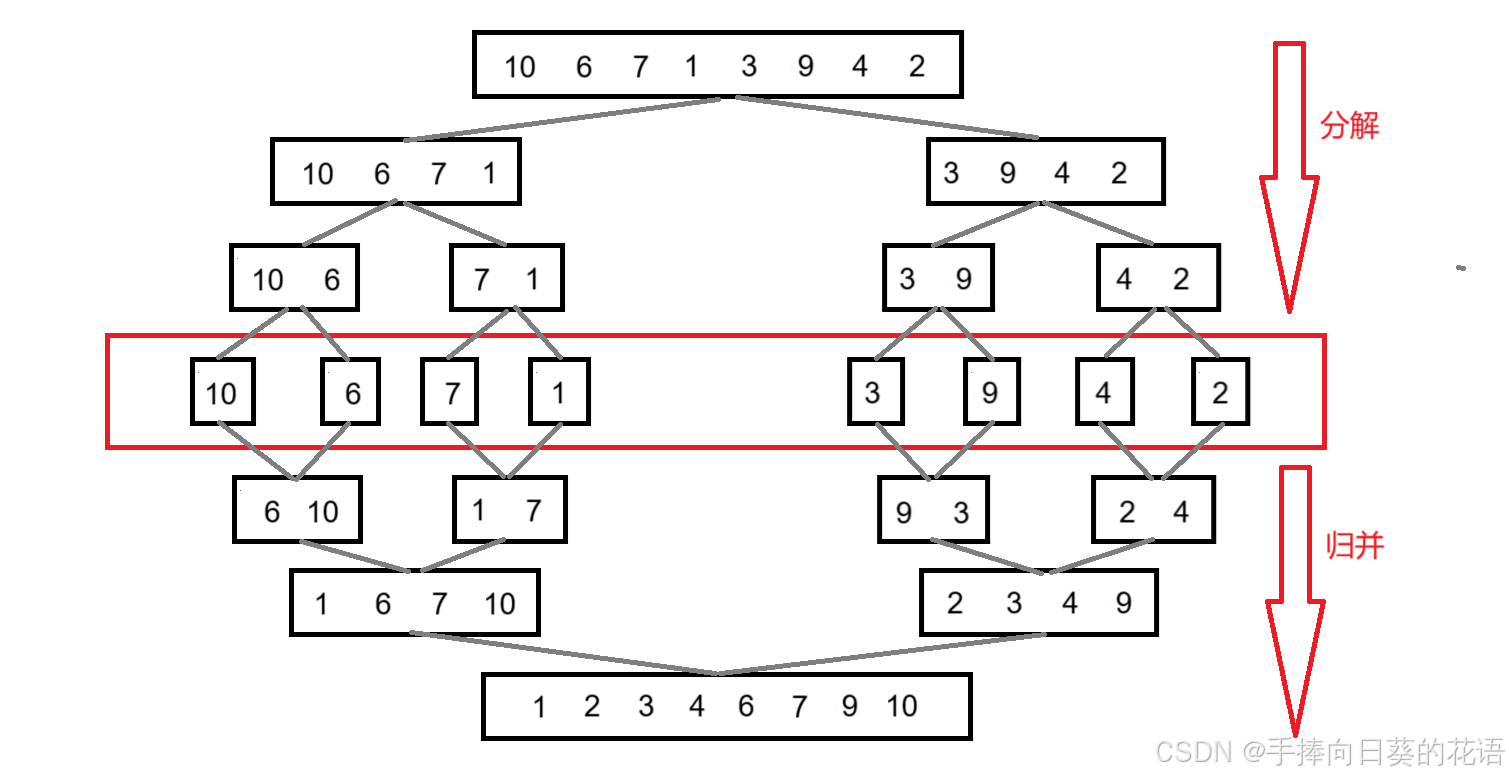
归并排序是一种建立在归并两个有序数组操作上的排序方法,该排序算法是分治的一个典型应用。其基本思想是:
- 先将待排序的有序序列的每个元素组成的数组看成是一个待归并的数组。
- 依次将效相邻的两个数组进行二路归并操作,合成一个更大有序的数组。
- 然后将得到的更大的且相邻的有序数组再归并成更大的有序数组,直到将整个数组的元素贵宾成有序的。
归并排序动图演示
2.归并排序的递归实现
归并排序的遍历方式
从上图可以看出,归并排序也是一种类似于二叉树结构的排序算法,所以,归并排序也可以根据二叉树的遍历来实现,那我们采用二叉树的前序、中序还是后续来实现呢?
我们可以分析一下:
- 归并排序归并的是两个待排序的序列。
- 如果我们使用前序遍历,第一个待排序的序列就是整个数组中的元素,此时只有一个待排序的序列,无法进行归并。
- 如果我们使用中序遍历,排完左边的子序列之后,就需要排根,此时的根是两个子序列并集,子序列不符合要求,无法进行排序。
- 如果我们使用后续遍历,将待排序的序列分为左右子序列之后,再将左右子序列归并,符合要求。
所以,归并排序的递归实现,我们采用后续遍历。
归并排序的归并流程
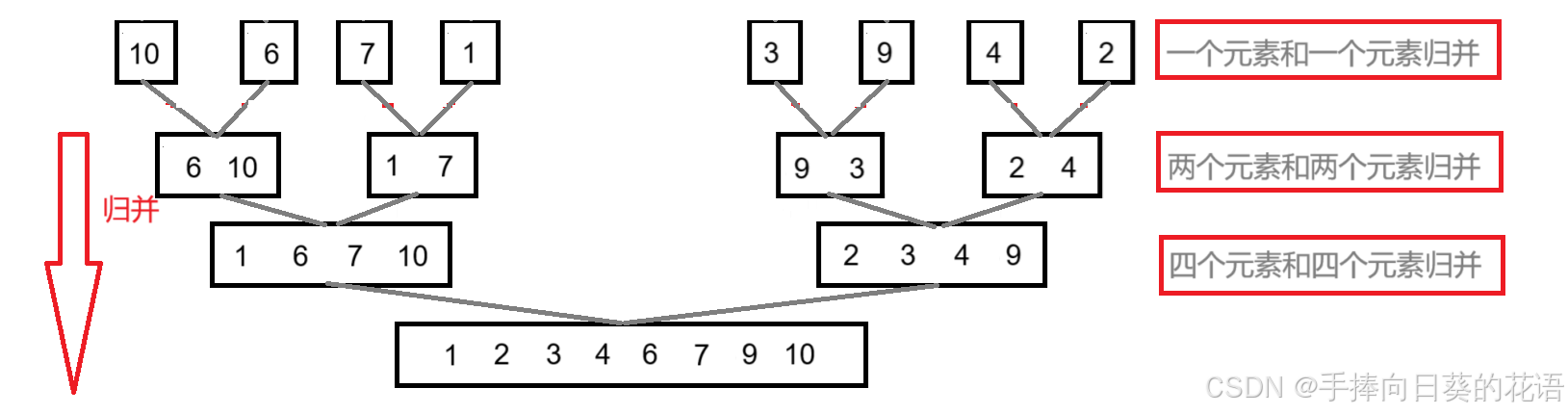
我们再来看一看归并排序的归并过程:
首先是一个元素和一个元素归并,归并完成之后,两个元素和两个元素归并,然后,四个元素和四个元素归并;不管是几个元素和几个元素归并,核心都是左右两个有序序列进行归并。所以,我们需要先将待排序序列分成一个元素和一个元素归并的情况,然后是两个元素和两个元素归并……
我们可以通过递归来划分左右子序列,代码如下所示:
- 当 end < begin 的时候,区间不存在,函数退出;当end==begin的时候,此时计算出的mid和end、begin是一样的,说明左右子序列相同,并且只有一个元素,不需要归并。
- 因为我们的代码中是通过 (end+begin) / 2 来计算mid的,递归到叶子结点的时候,左右子序列一定只有一个值。
- 于是我们就可以先将一个元素和一个元素进行归并,值得一提的是,一个元素直接就是有序,符合归并有序数组的前提。一个元素和一个元素归并完之后就获得了一个具有两个元素的有序序列。
- 然后在重复该过程,直到待排序序列有序。
归并排序的递归代码实现
前面说过,我们可以根据begin和end以及begin和end的中间值mid,划分出左子序列和右子序列,然后归并左右子序列即可。
需要注意的是:归并过程需要借助新的数组来完成,这样实现起来比较方便。
void _MergeSort(int* a, int* tmp, int begin, int end)
{
if (end <= begin)
return;
int mid = (end + begin) / 2;
// [begin, mid][mid+1, end]
_MergeSort(a, tmp, begin, mid); //递归左子树
_MergeSort(a, tmp, mid+1, end); //递归右子树
// 执行归并过程
// 归并到tmp数据组,再拷贝回去
// a->[begin, mid][mid+1, end]->tmp
int begin1 = begin, end1 = mid;
int begin2 = mid+1, end2 = end;
int index = begin;
while (begin1 <= end1 && begin2 <= end2) // 选小的尾插
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1) //左区间有剩余元素,尾插左区间的剩余元素
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) //右区间有剩余元素,尾插右区间的剩余元素
{
tmp[index++] = a[begin2++];
}
// 拷贝回原数组
memcpy(a + begin, tmp + begin, (end - begin + 1)*sizeof(int));
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
_MergeSort(a, tmp, 0, n - 1);
free(tmp);
}3.归并排序的非递归实现
非递归实现分析
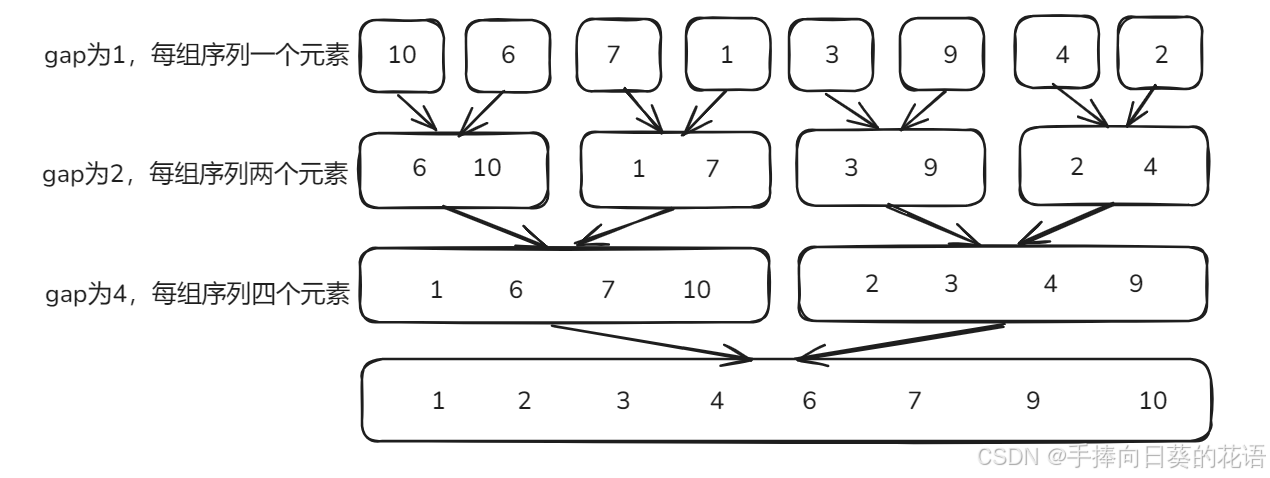
用非递归实现归并排序,和递归实现归并排序相比,不需要进行递归分解,但是同样需要划分左右子序列,只是划分的方式不一样,在非递归中,我们通过一个变量gap来实现,gap为几,子序列中就有几个元素(元素不够gap个的情况后面分析)
注意:用非递归代码实现归并排序,我们同样需要借助一个新的数组空间来完成。
非递归实现归并排序步骤如下:
- 开辟新的数组空间。
- 定义gap,gap初识为1,表示一个元素和一个元素进行归并。
- 将结果归并到新数组中,然后拷贝回原数组。
- gap增大为原来的两倍,继续归并到新数组中,归并完之后拷贝回原数组。
- 直到gap >= 数据个数,表示不能划分出两组用来归并的子序列了,整个归并排序排完,待排序序列变得有序。
边界分析
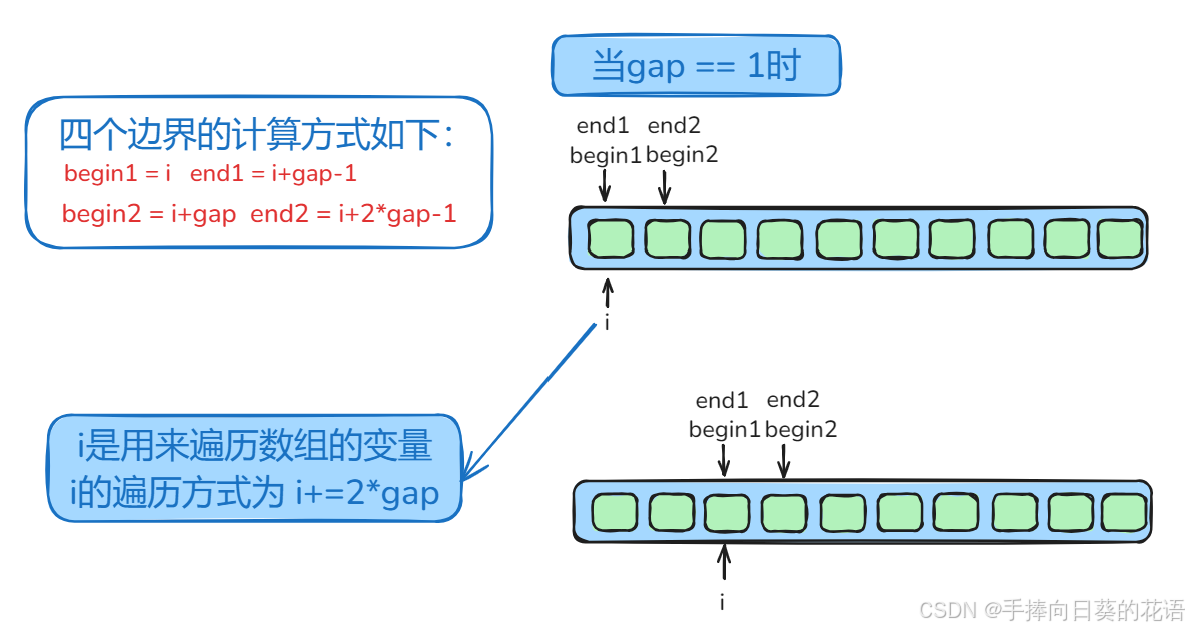
我们划分左右子序列边界的时候,左子序列的边界是 [begin1,end1],右子序列边界为[begin2,end2];我们使用变量i来遍历数组,于是四个边界的计算方式如下:
- begin1 = i end1 = i+gap-1;begin2 = i+gap end2 = i+2*gap-1;
- 变量i的变化为 i += 2*gap。
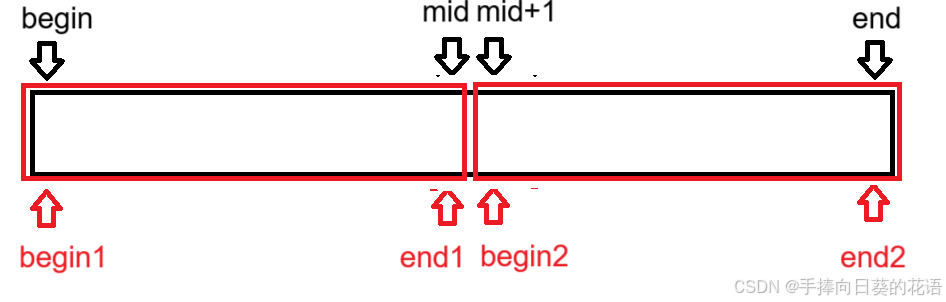
下图演示了边界控制:
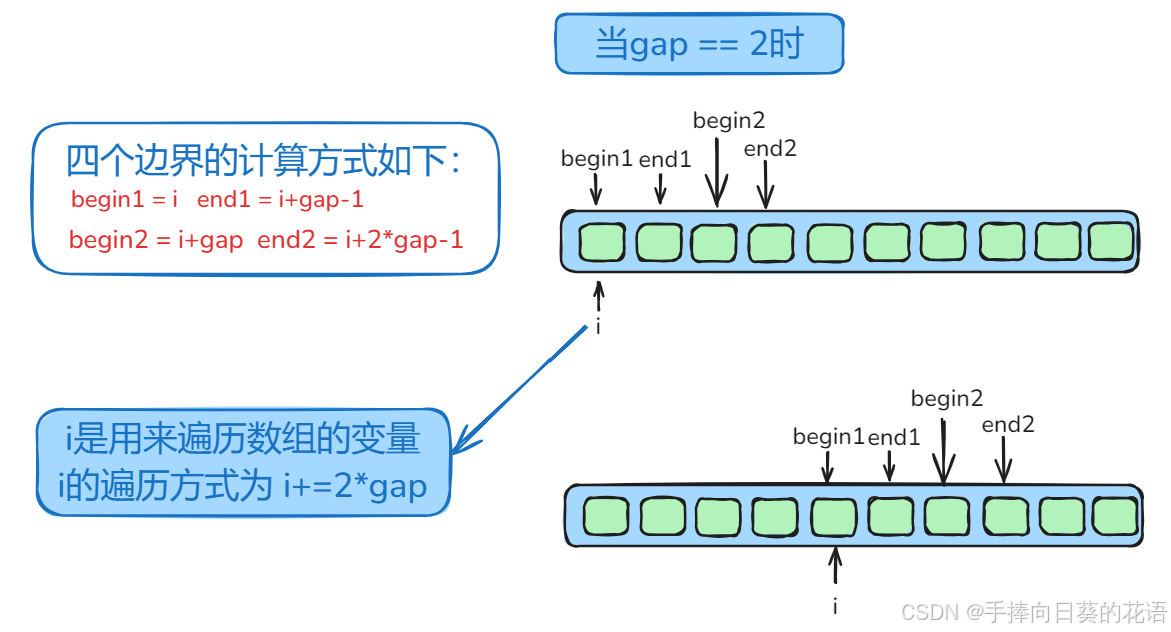
- 对于begin1来说,begin1 = i,i由我们控制的,i < n(数据个数),所以,begin1是不会越界的。
- end1,begin2,end2都在i的基础上增加了值,所以,这三个变量是可能会越界的。
- 当end1越界时,也就是end1 >= n,说明左区间越界,此时,肯定不存在右区间,所以这一趟是无法归并的,直接跳出循环即可。
- 当begin2越界时,也就是begin2 >= n,说明用于归并的右区间不存在,这种情况和end1越界是一样的,直接跳出循环。
- 当end2越界,也就是end2 >= n说明右区间存在,但是右区间越界了,修正一下就好了,也就是将end2的赋值为n-1。
边界情况弄清楚之后,代码就很好写了。
非递归实现代码
void MergeSortNonR(int* a, int n)
{
// 开辟新的数组空间
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
int gap = 1;
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// [begin1,end1] [begin2,end2] 归并
// 如果第二组不存在,这一组不用归并了
if (begin2 >= n)
{
break;
}
// 如果第二组的右边界越界,修正一下
if (end2 >= n)
{
end2 = n - 1;
}
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
// 拷贝回原数组
memcpy(a + i, tmp + i, (end2-i+1) * sizeof(int));
}
// gap每次扩大二倍
gap *= 2;
}
free(tmp);
}4.归并排序总结
时间复杂度
归并排序的时间复杂度分析类似于快速排序,同样属于二叉树结构的排序方式,每一层遍历N次,树的高度为logN。所以,归并排序的时间复杂度为N*logN。
空间复杂度
在归并排序的过程中,无论是递归代码还是非递归代码,都开辟了额外的数组空间,所以,时间复杂度是O(N)。
稳定性
归并排序采用在有序数组中,元素两两比较的方式,可以做到稳定。