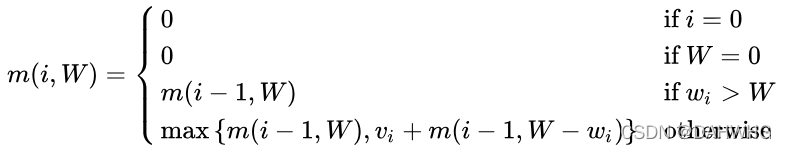DP问题的核心即确定动态转移方程。
(1)寻找变量,确定子问题。DP表一般为二维,故需要两个变量。
(2)寻找总问题与子问题迭代关系,确定中间值、迭代值
例1:
有5个物品,其重量分别是{2, 2, 6, 5, 4},价值分别为{6, 3, 5, 4, 6},背包的容量为10,计算背包所能装入物品的最大价值。
(1)寻找变量
在这个问题中,每个物品所对应的重量与价值是确定的。故将物品数量与可分配容量作为变量。
总问题转化为在前5件物品中挑选容量不超过10的物品,使价值最大。
子问题转化为在前
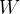
(2)迭代关系
状态值:最大价值
DP表中状态值一般包含两种情形:当前问题仍保留前一个状态值作最优解;通过中间值更新当前问题的最优解。通过第二种情形可以确定所有子问题的最优解。
中间值:更新当前问题的最优解时,需要对前一个状态值累加中间值。背包问题的中间值就是更新最优解时加入物品的价值。
存在两种情况:
(1)如果第i个物品没有装入背包,则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。而第一种情况又可以细分为以下两种情况
① 背包可分配容量不够
② 可以加入背包,但加入后的总价值低于不加入时只考虑前i-1个物品的总价值,即不加入此物品可以更好的分配其他物品从而获得最优解。
(2)如果把第i个物品装入背包,则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi;