在帖子“给大家分享我自己编的程序-连续小波变换” 中，pengzk版友给出了morlet小波变换的源代码，但其中的许多参数和语句意义不够明确，这就给一些希望了解连续小波变换实现方法的版友带来不便。因此，本帖将对连续小波变换的实现原理做个小结，希望对各位有所帮助。

首先说明的是，在Matlab的小波工具箱和pengzk版友提供的程序中，连续小波变换都是依据以下原理实现的：连续小波变换可以看成是原信号与小波基进行卷积的结果。

下面我以自编的连续morlet小波变换程序为例说明利用卷积方法实现连续小波变换的过程(参见程序注释)。其中，所用morlet小波的定义为

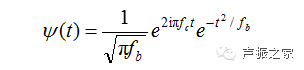
程序如下：

function wcoefs = mymorletcwt(Sig,Scales,fc,fb)

%==================%

% Continuous Wavelet Transform using Morlet function

%======输入======%

% Sig: 输入信号

% Scales: 输入的尺度序列

% fc: morlet小波中心频率 (默认为2)

% fb: morlet小波带宽参数 (默认为2)

%======输出======%

% wcoefs: morlet小波变换计算结果

%==================%

if (nargin <= 1),

error('At least 2 parameters required');

end;

if (nargin < 4),

fb = 2;

elseif (nargin < 3),

fc = 2;

end;

wavsupport=8;

% 默认morlet小波的支撑区为[-8,8]

nLevel=length(Scales);

% 尺度的数目

SigLen = length(Sig);

% 信号的长度

wcoefs = zeros(nLevel, SigLen); 

% 分配计算结果的存储单元

for m = 1:nLevel

% 计算各尺度上的小波系数

a = Scales(m);

% 提取尺度参数

t = -round(a*wavsupport):1:round(a*wavsupport);

% 在尺度a的伸缩作用下，此时小波函数的支撑区会变为[-a*wavsup,a*wavsup]，采样频率为1Hz

Morl = fliplr((pi*fb)^(-1/2)*exp(i*2*pi*fc*t/a).*exp(-t.^2/(fb*a^2)));

% 计算当前尺度下的小波函数，按小波变换的定义这里需要倒置

temp = conv(Sig,Morl) / sqrt(a);

% 计算信号与当前尺度下小波函数的卷积

d=