数据分析之正态性检验

定义

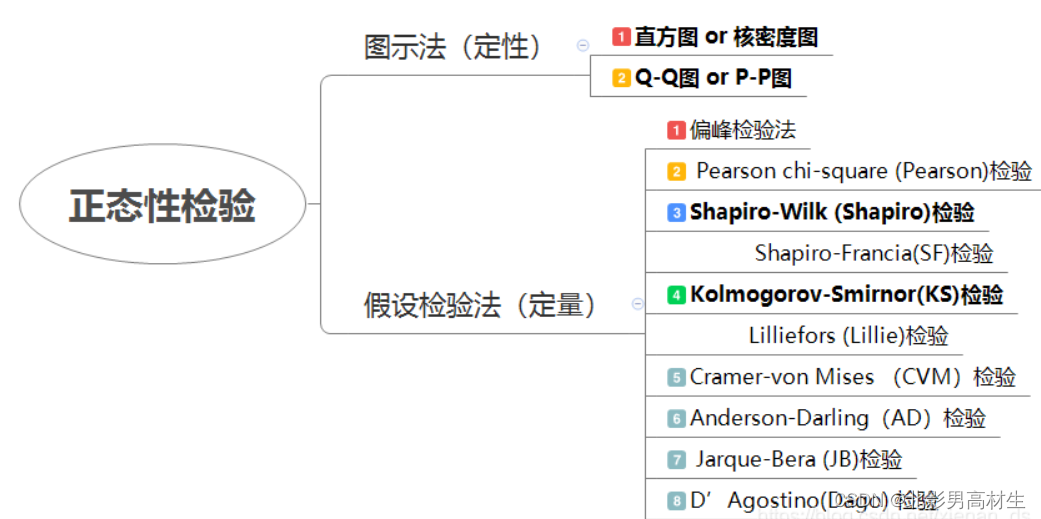
利用观测数据判断总体是否服从正态分布的检验称为正态性检验，它是统计判决中重要的一种特殊的拟合优度假设检验。常用的正态性检验方法有正态概率纸法、夏皮罗一威尔克检验法(Shapiro-Wilktest)，科尔莫戈罗夫检验法，偏度-峰度检验法等。

在数据分析过程中，数据的不同分布形态将直接影响数据分析策略的选择。因此，对数据分布形态的判定是非常重要内容。常见的数据分布形态有正态分布、均匀分布、指数分布、泊松分布等。但最重要也是最有用的分布形态是正态分布，很多数据分析技术都是面向正态分布的定距变量。

下面介绍数据正态性的几种判断方法，这些方法其实也适用于其它分布。在Excel中没有数据分布形态判断的功能，但是SPSS中有丰富判断工具。理解判断方法的理论依据是做出正确方法选择的基础，掌握理论再借助SPSS等软件的快速计算展现就能事半功倍。

正态性检验主要有三种：偏度和峰度，图示法，非参数检验

————————————————
本图链接：https://blog.csdn.net/xienan_ds_zj/article/details/90340080

1、偏度和峰度

python 求偏度和峰度

import pandas as pd
import numpy as np
data1 = list(np.random.randn(10000))
SK = pd.Series(data1).skew()#偏度
K  = pd.Series(data).kurt()#峰度

1.1 偏度

偏度（Skewness）：描述数据分布不对称的方向及其程度，是指数据分布偏斜程度。使用偏态系数(SK)来测度数据的偏态

偏态系数以平均值与中位数之差对标准差之比率来衡量偏斜的程度，用SK表示偏斜系数:偏态系数小于0，因为平均数在众数之左，是一种左偏的分布，又称为负偏。偏态系数大于0，因为均值在众数之右，是一种右偏的分布，又称为正偏。

偏态系数是根据众数、中位数与均值各自的性质，通过比较众数或中位数与均值来衡量偏斜度的，即偏态系数是对分布偏斜方向和程度的刻画。一般认为，没有百年以上的资料，偏态系数的计算结果很难得到一个合理的数值。

偏态 SK = (sum(x-mean)^3) /(n*std^3)

1.1.1 判断是否存在

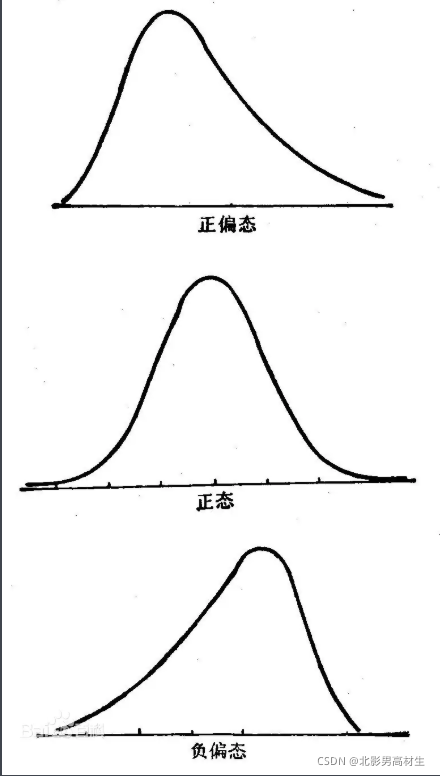
当偏度≈0时，可认为分布近似服从正态分布；
当偏度>0时，分布为右偏，称为正偏态；
当偏度<0时，分布为左偏，称为负偏态；

注：偏度的判断不是看峰尖的偏向而是看拖尾的偏向，拖尾在左即是左偏态（负偏态），拖尾在右即为右偏态（正偏态）
在这里插入图片描述

1.1.2 偏态（SK）的程度

0<|SK|<=0.5 低度偏态分布
0.5<|SK|<=1 中等偏态分布
|SK|>1 高度偏态分布

1.1.3 偏态对众数、中位数和均值之间关系的影响

对称分布：均值=中位数=众数
左偏分布：均值<中位数<众数
右偏分布：众数<中位数<均值

1.2 峰度

峰度（Kurtosis）：描述数据分布形态的陡缓程度。使用峰态系数(K)来测度数据的偏态

1.2.1 判断是否存在

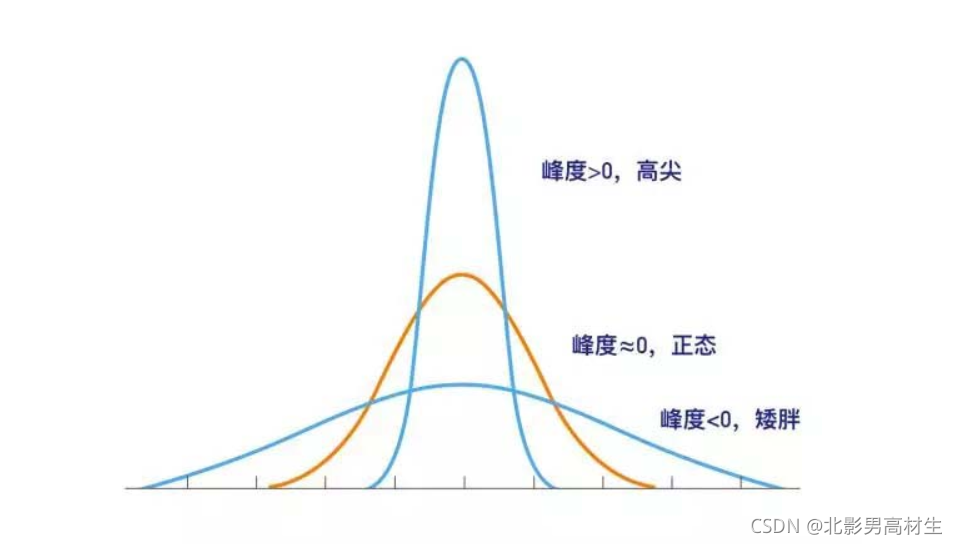
当峰度≈0时，可认为分布近似服从正态分布；
当峰度>0时，尖峰分布；
当峰度<0时，扁平分布；

在这里插入图片描述

1.2.2 峰态（K）的程度

0<|K|<=0.5 低度尖峰分布
0.5<|K|<=1 中等尖峰分布
|K|>1 高度尖峰分布

1.3 用偏度和峰度判断正态性（Z-score）

利用偏度和峰度进行正态性检验时，可以同时计算其相应的Z评分（Z-score）

偏度：Z-score=偏度值/标准误
峰度：Z-score=峰度值/标准误

在α=0.05的检验水平下，若Z-score在±1.96之间，则可认为数据近似服从正态分布

2、图示法

2.1 直方图：可以直观显示数据的分布形式

直方图(histogram)是用于展示分组数据分布的一种图形，它是用矩形的宽度和高度（即面积）来表示频数分布的。绘制该图时，在平面直角坐标系中，用横轴表示数据分组，纵轴表示频数或频率，这样就形成了一个矩形（即直方图）。
直方图与柱状图的区别：
①直方图的高度与宽度都有意义。柱状图是用柱子的长度表示各类别频数的多少，其宽度（表示类别）固定；而直方图是用面积表示各组频数的多少，矩形的高度表示每一组的频数或频率，宽度则表示各组的组距；
②由于分组数据具有连续性，直方图的各矩形通常是连续排列，而柱状图则是分开排列；
③柱状图用于展示分类型数据，直方图用于展示数值型数据。
————————————————
原文链接：https://blog.csdn.net/xienan_ds_zj/article/details/90340080

2.2 P-P图

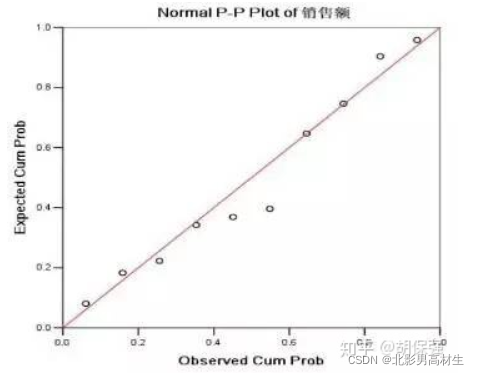
P-P图是根据变量的累积比例与指定分布的累积比例之间的关系所绘制的图形（P是累积比例单词的首字母）。当数据符合指定分布时，P-P图中各点近似一条直线。以样本的累积频率作为横坐标，以按照正态分布计算的相应累积频率作为纵坐标。举例如下图：

从上图可以判断数据序列是正态分布的。
————————————————
原文链接：https://zhuanlan.zhihu.com/p/49456086

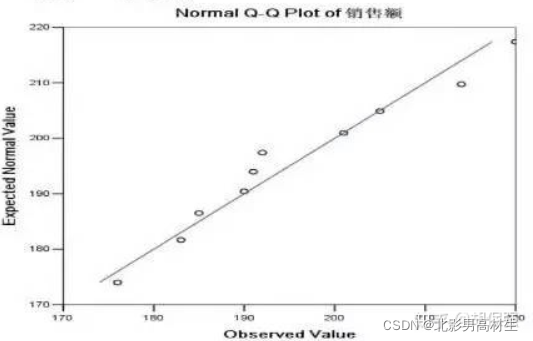
2.2、Q-Q图

Q-Q图与P-P图类似，只不过Q-Q图是以分位数作为横纵坐标。它用标准正态分布的分位数作为横坐标，样本值作为纵坐标。利用Q-Q图鉴别样本数据是否近似于正态分布，只需看图上的点是否在一条直线附近，如下图：

P-P图和Q-Q图的判断精度比主观判断法的精度更高，但仍然没有量化判断标准，所以还是将它们归类为主观判断的范畴。
————————————————
原文链接：https://zhuanlan.zhihu.com/p/49456086

P-P图反映了变量的实际累积概率与理论累积概率的符合程度，Q-Q图反映了变量的实际分布与理论分布的符合程度，两者意义相似，都可以用来考察数据是否服从某种分布类型。若数据服从正态分布，则数据点应与理论直线基本重合。

2.3 python 实现

# QQ图
import statsmodels.api as sm
sm.qqplot(y,line='s')

# PP图
from scipy import stats
stats.probplot(x, dist="norm", plot=plt)

3、非参数检验

正态性检验属于非参数检验，原假设为“样本来自的总体与正态分布无显著性差异”，只有P>0.05才能接受原假设，及数据符合正态分布。

一般常用的检验方法有两种(常用，还有其他的方法)，Shapiro-Wilk检验Kolmogorov–Smirnov检验，前者适用于小样本数据，后者适用于大样本数据。

3.1 Shapiro-Wilk test（S-W检验）

属于专门用来做正态性检验的模块
其原假设：样本数据符合正态分布。
注：适用于小样本

S,P = scipy.stats.shapiro(x)

x参数为样本值序列，返回值中第一个为检验统计量，第二个为P值，当P值大于指定的显著性水平，则接受原假设。

3.2 Kolmogorov-Smirnov（K-S检验）

可以检验多种分布，不止正态分布
其原假设：数据符合正态分布
注：适用于大样本

K,P = scipy.stats.kstest(rvs,cdf,alternative,mode)

rvs：待检验数据。
cdf：检验分布，例如’norm’，‘expon’，‘rayleigh’，'gamma’等分布，设置为’norm’时表示正态分布。
alternative：默认为双侧检验，可以设置为’less’或’greater’作单侧检验。
model:‘approx’(默认值)，表示使用检验统计量的精确分布的近视值；‘asymp’：使用检验统计量的渐进分布。
其返回值中第一个为统计量，第二个为P值。

3.3 其他正态性检验-1

N,P= scipy.stats.normaltest(a,axis,nan_policy)

其原假设：样本来自正态分布

a 待检验的数据
axis=None 可以表示对整个数据做检验，默认值是0。
nan_policy：当输入的数据中有nan时，‘propagate’，返回空值；‘raise’ 时，抛出错误；‘omit’ 时，忽略空值。
其返回值中，第一个是统计量，第二个是P值。

3.3 其他正态性检验-2

A,C,P = scipy.stats.anderson(x,dist)

由 scipy.stats.kstest 改进而来，用于检验样本是否属于某一分布（正态分布、指数分布、logistic 或者 Gumbel等分布）

x表示样本数据。
dist表示分布，有’norm’,‘expon’,‘logistic’,‘gumbel’,‘gumbel_l’, gumbel_r’,‘extreme1’
返回值有三个，第一个表示统计值，第二个表示评价值，第三个是显著性水平；评价值和显著性水平对应。对于不同的分布，显著性水平不一样。
关于统计值与评价值的对比：当统计值大于这些评价值时，表示在对应的显著性水平下，原假设被拒绝，即不属于某分布。

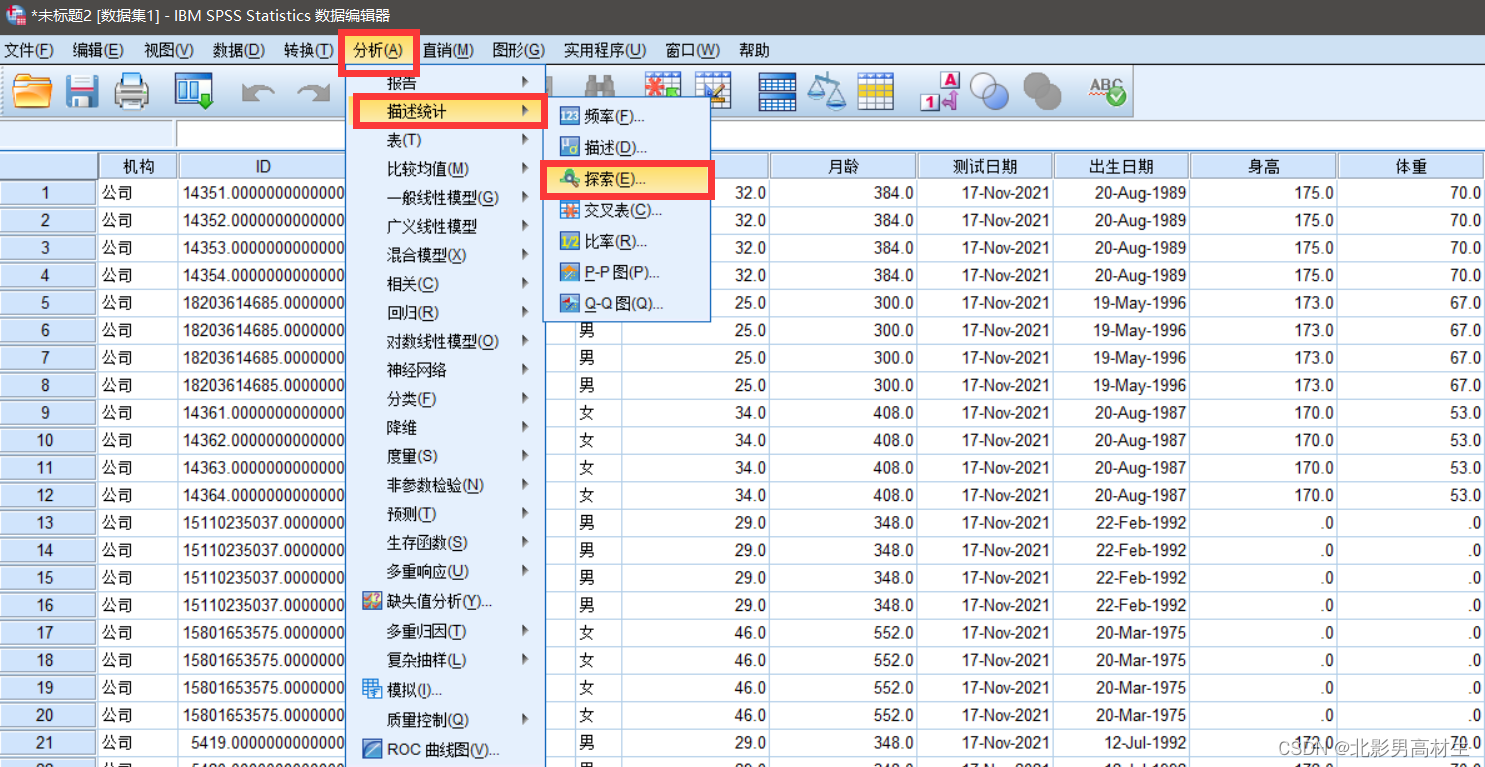
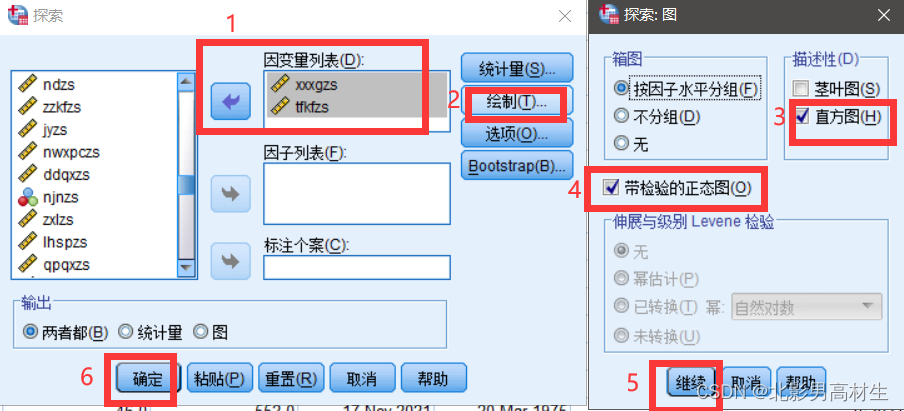
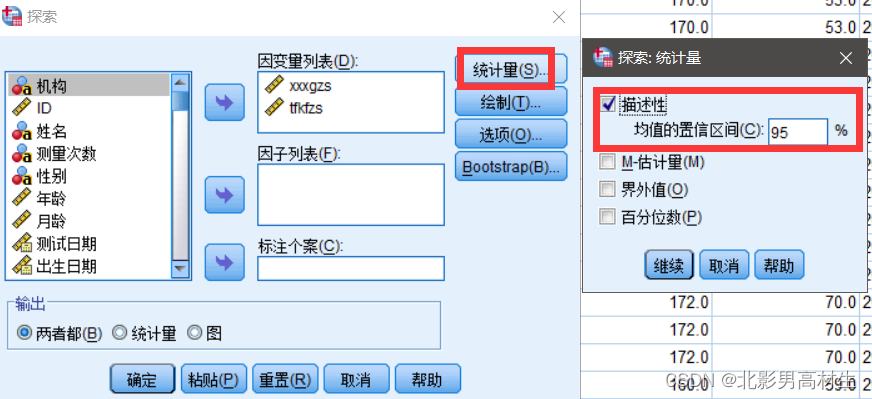
4、使用SPSS进行正态性检验

4.1 正态性判断-1（KS、SW检验）

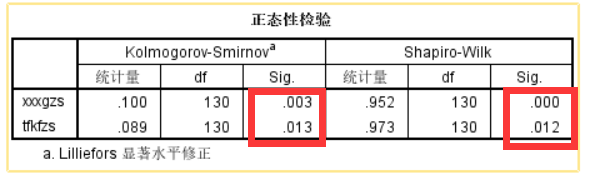
在这里插入图片描述

此为P值，当P值大于指定的显著性水平，则接受原假设（原假设为：样本来自正态分布），大于设定值（自己可以设置，一般为0.05或0.01）时则代表接受原假设，我这里设置的是0.05；本组数据样本量为130，故此处用大样本正态性检验KS，xxxgzs的P值小于设定值0.05，则拒绝原假设，说明xxxgzs不是正态分布，tfkfzs的P值也小于0.05，拒绝原假设，说明tfkfzs也不是正态分布。

关于大样本和小样本的问题，这直接关系到所用的正态检验方法，一般认为大于100条（也有说50条或30条）则为大样本，但面对不同情况、不同数据，需要具体分析。

KS检验适用于大样本，SW检验适用于小样本

若仍不理解，可参考链接：SPSS 统计分析策略（1）：正态性检验与判断

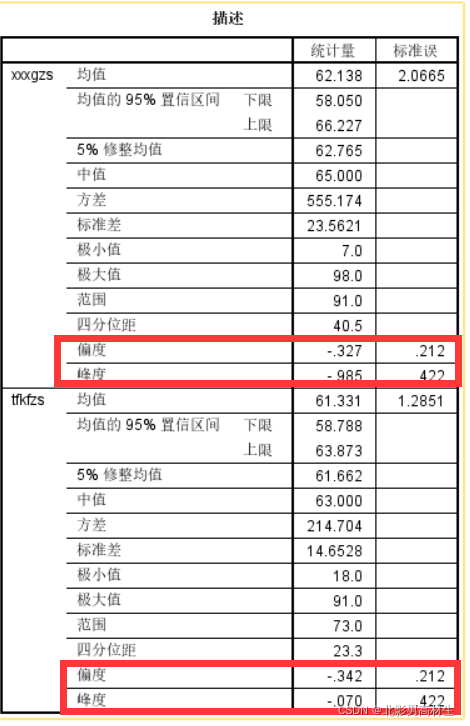
4.2 正态性判断-2（偏度、峰度判断）

xxxgzs

偏度：Z-score = （-0.327）/0.212 = -1.542 峰度：Z-score = （-0.985）/0.422 = -2.334

tfkfzs

偏度：Z-score = （-0.342）/0.212 = -1.613 峰度：Z-score = （-0.070）/0.422 = -0.166

计算规则请参考上面偏度、峰度介绍
（在α=0.05的检验水平下，Z-score在±1.96之间，若都满足则可认为服从正态分布，若一个不满足则认为不服从正态分布） 参考链接：https://zhuanlan.zhihu.com/p/53184516/

根据偏度和峰度的Z-score 结果可知，xxxgzs 不满足正态，这与KS检验结果一致；但tfkfzs根据Z-score可知满足正态分布，这与KS检验结论不一致。

关于这个问题，答主查找了许多资料但都没有明确说明两种检验方法不一致这种情况的，但搜到了一些关于偏度和峰度的一些使用条件或是说判别方法：

理论上讲，标准正态分布偏度和峰度均为0，但现实中数据无法满足标准正态分布，因而如果峰度绝对值小于10并且偏度绝对值小于3，则说明数据虽然不是绝对正态，但基本可接受为正态分布。参考链接：https://zhuanlan.zhihu.com/p/70755099
偏度和峰度的适用条件为：样本量小于30时，使用偏度和峰度来判断正态性较好

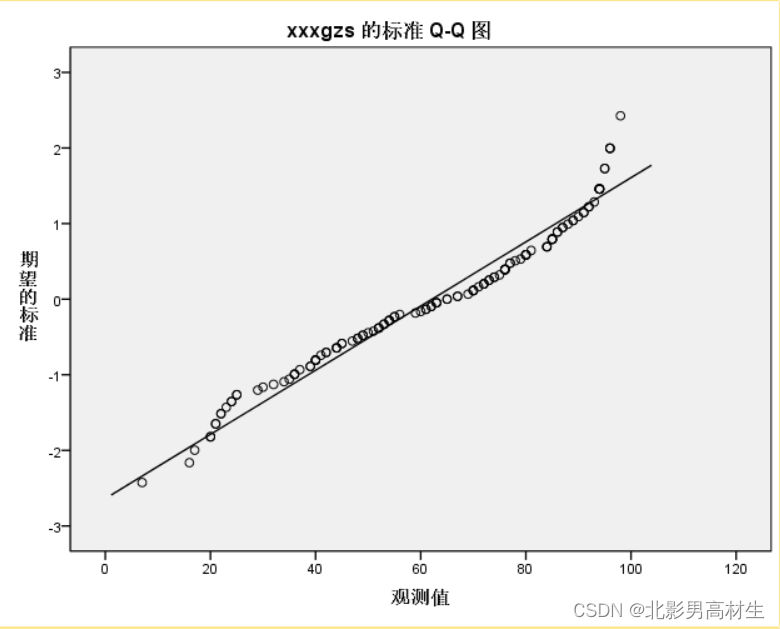
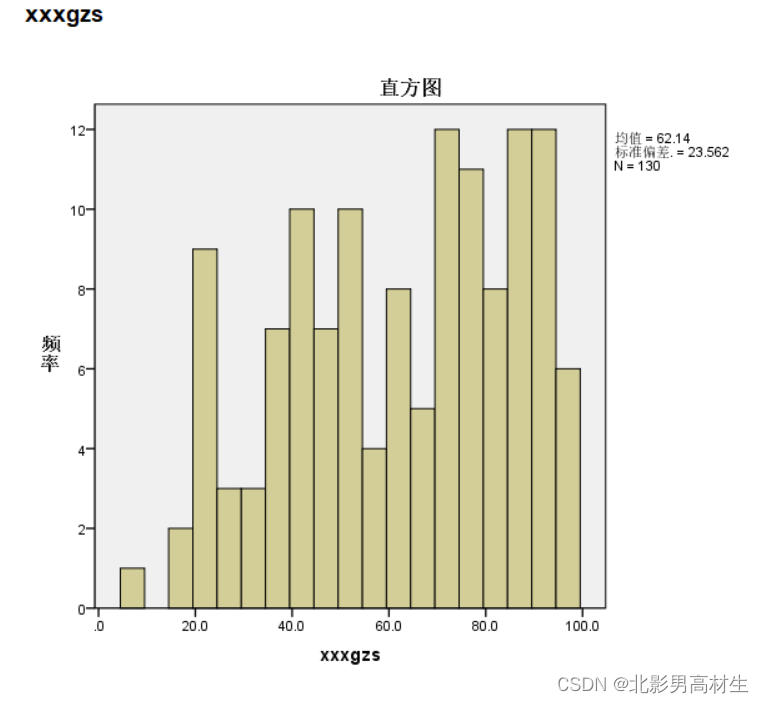
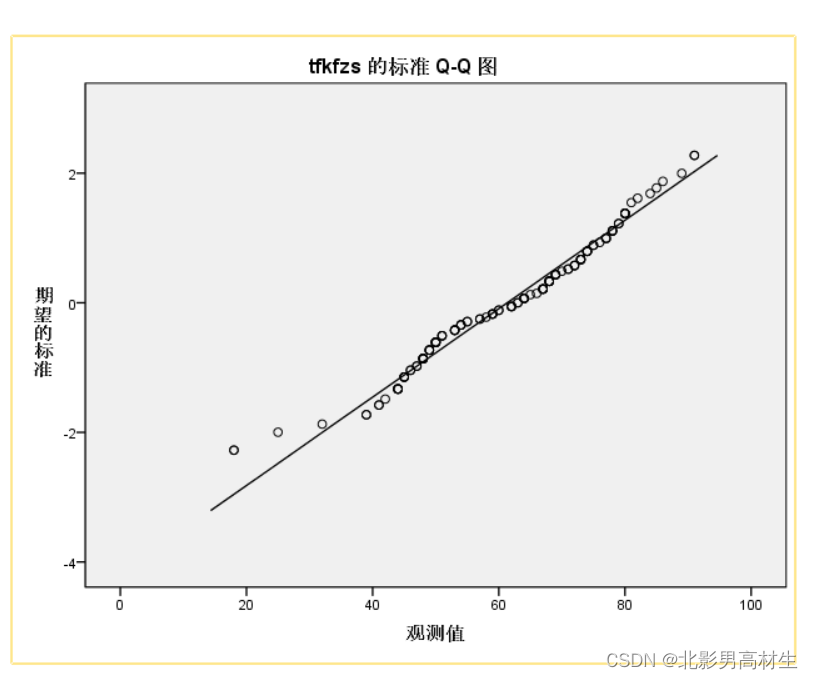
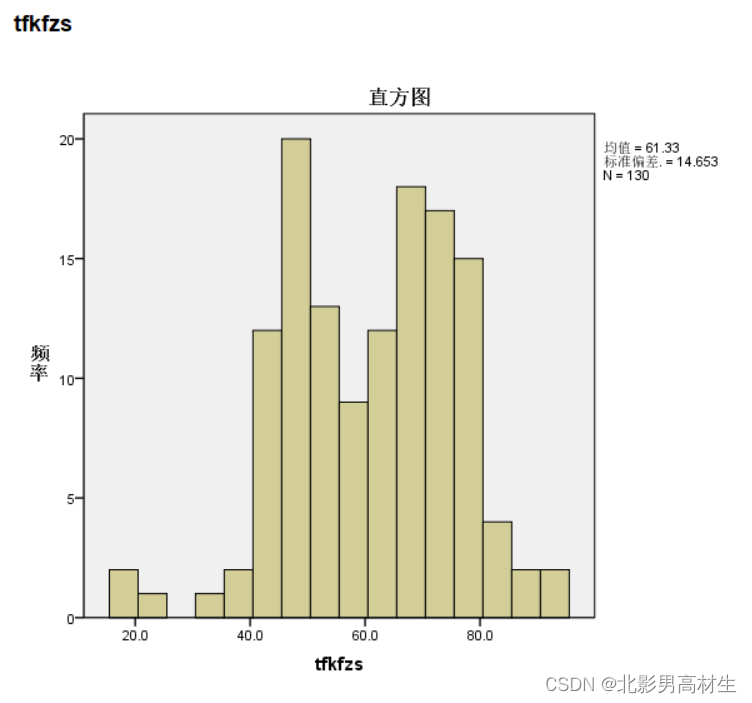
4.3 正态性判断-3（Q-Q图，直方图）

在这里插入图片描述

Q-Q图或P-P图对于一些临界正态性的判断太过主观，就像上面的Q-Q图，严格来讲的话都不算是正态性样本，但若粗略来看tfkfzs也可勉强算是正态性样本数据。我更偏向使用的是KS检验或SW检验，从结果来讲比较明显，可以直接判断是否符合正态性。

由于我很少用Q-Q或P-P图，仅看过一些文献，对其认知还是有些浅薄，观者可不用参考此处判断，此处描述只是为了告诉大家有这样的正态性判断的方法。

注：若有需要中文版SPSS分析软件的可私信答主，文件大小：980M（仅供学习使用）

以上

若以后有新的内容再做补充