复现结果

在 PointGoal1、CarGoal1、Velocity-Walker2d 三个任务上测试了 RCPO，CRPO 以及 Safe-Policy-Optimization 中实现的 CPO，PPO-Lag 算法。

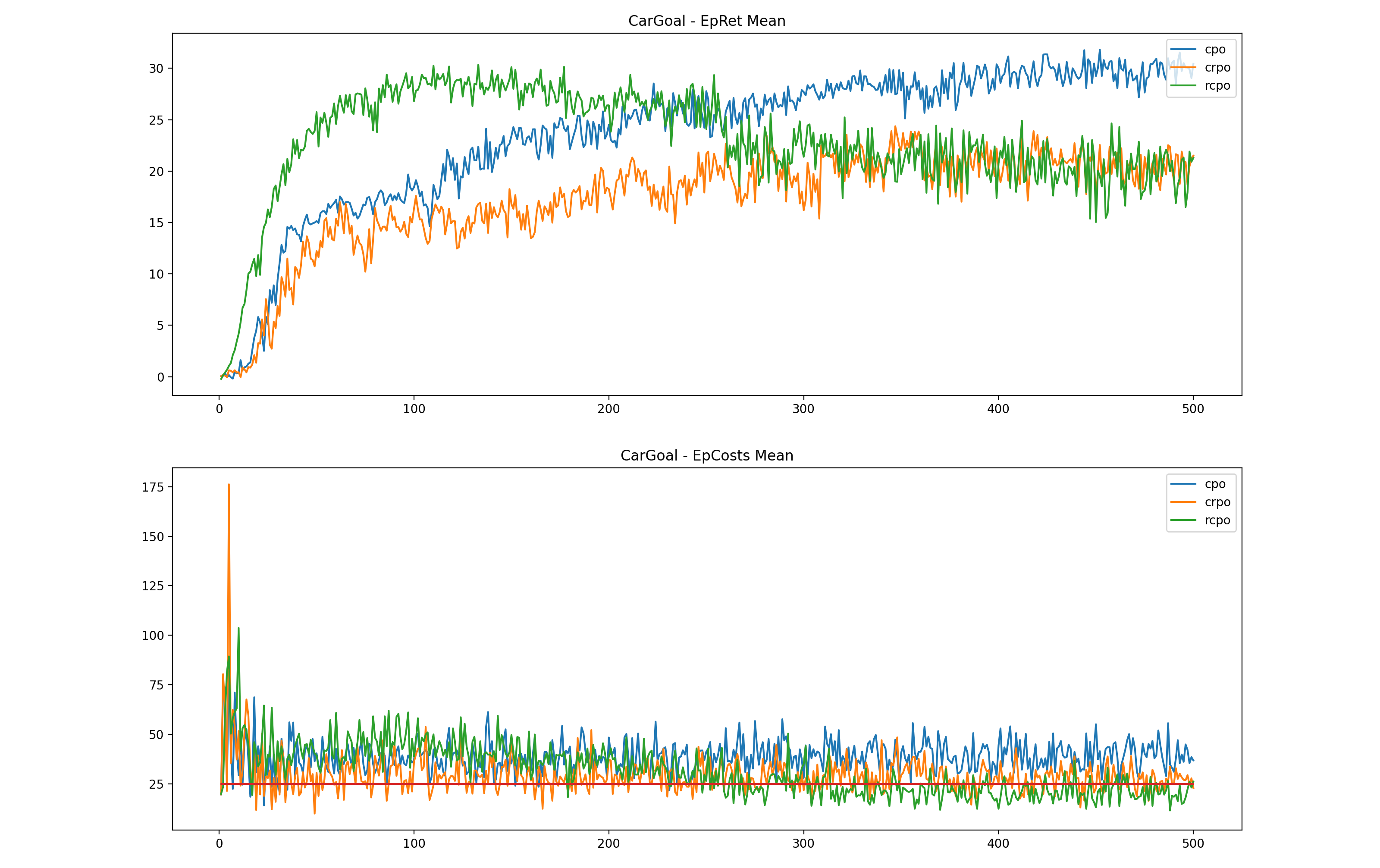
CarGoal

PointGoal

PointGoal1 和 CarGoal1 任务相对比较困难，在探索初期就很容易违反约束。

PPO-Lag 和 TRPO-Lag 都不能得到满足约束的解，故没有在途中画出。

使用 RCPO 将拉格朗日乘子初值设置为 2 之后，可以跑出可行解，但是 reward 不高，且仍然会出现震荡的现象。

使用 CRPO 可以跑出可行解，reward 与 RCPO 持平，后面会对其进行修改。

另外尝试使用 CPO，发现虽然 reward 最高，但是得不到可行解。

Walker2d

在 Velocity-Walker2d 中使用 ppo-lag 会产生周期性的震荡。原因是 KaTeX parse error: Undefined control sequence: \part at position 7: \frac{\̲p̲a̲r̲t̲ ̲L}{\part\lambda…，而 $\lambda$ 增大又会使得 EpCosts 减小。如果 $\lambda$ 更新过快，就会导致这两个过程的时间差较长，从而产生周期较大的波动。

这个任务比较简单，其他的算法差别不大。

对CRPO的改进

在PointGoal1 和 CarGoal1中发现 CRPO 训练过程中不稳定，而且训练到一定程度的时候 reward 难以继续提高。因为这两个任务的约束比较强，即使在没有充分探索的前期就很容易违反约束。CRPO 在违反约束时立即转向，导致很容易被束缚住而探索不到好的策略。同时，cost 负梯度和 reward 梯度的方向一般是相反的，就会导致参数发生震荡。

因此做了两点改进：

1. 减小学习率。
2. 在违反约束时参数更新方向不再是单一的减小 cost 的方向，而是 cost 的负梯度 * alpha + reward 的梯度 * （1-alpha）

第 2 点中的 alpha 尝试了固定值（0.7，0.85）以及自适应值（类似 PDO 更新拉格朗日乘子），发现自适应的更新 alpha 效果更好，与改进前相比，前期训练表现提升较快，也能得到满足约束的解，并且 reward 有较大提高。当然，与标准的 CRPO 相比这会导致训练过程中存在违反约束的时间增加。

CarGoal

PointGoal

思考

构造拉格朗日函数：
$$L(\theta ,\lambda )=J_R^{{\pi }_{\theta }}-\lambda \cdot (J_C^{{\pi }_{\theta }}-d)$$
原问题等价于如下无约束问题：

$$\underset{\theta }{\max }\underset{\lambda \ge 0}{\min }L(\theta ,\lambda )$$
其拉格朗日对偶问题是原问题的一个上界：

$$\underset{\lambda \ge 0}{\min }\underset{\theta }{\max }L(\theta ,\lambda )$$
PDO 以及 RCPO 优化的是对偶问题，用较快速度更新 $\theta$，较慢速度更新 $\lambda$。

而 CRPO 可以看作直接优化原问题：给定一个 $\theta$，如果约束都被满足，那么最优的 $\lambda$ 为 0，此时对 $\theta$ 求梯度就是 $J_R^{{\pi }_{\theta }}$ 对 $\theta$ 的梯度；如果有一个约束没有满足，那么对应的 $\lambda$ 会趋向无穷大，这时对 $\theta$ 求梯度就是 $J_C^{{\pi }_{\theta }}$ 对 $\theta$ 的梯度。

由此猜测对于多约束问题，除了论文中的随机挑选一个违反的约束进行优化，可能还可以同时优化所有违反的约束。

局限性

PDO，RCPO 也可以看作是 reward shaping 的方法。虽然不再需要手动调节参数，但是 lambda 初值和学习率设置不当会导致训练难以收敛。如果学习率过高，表现也会周期性波动；如果过低，就很难收敛到合法解。同样，如果 lambda 初值距离最优值太远，也会很难收敛到合法解。

而 CRPO 在训练后期震荡还是比较明显。