Transformer 中的 Decoder 机制

大家好，今天和各位分享一下 Transformer 中的 Decoder 部分涉及到的知识点：计算 self-attention 时用到的两种 mask。

本文是对前两篇文章的补充，强烈建议大家先看一下：

1.《Transformer代码复现》：https://blog.csdn.net/dgvv4/article/details/125491693

2.《Transformer中的Encoder机制》：https://blog.csdn.net/dgvv4/article/details/125507206

1. Decoder 的 self-attention 中的 mask

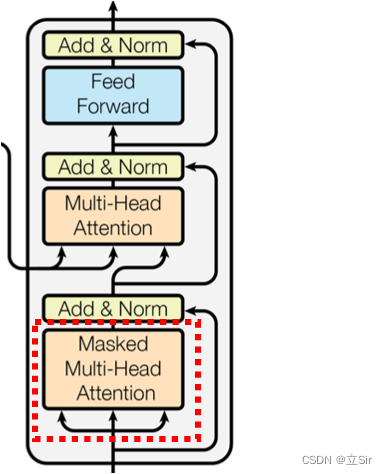
本节介绍的 mask 对应模型结构图中的位置：

如下图，decoder 的 self-attention 中使用的 mask 是一个下三角矩阵，当 decoder 预测第一个单词时，给它的输入是一个特殊字符 x1，当 decoder 预测第二个位置时，给它的输入是特殊字符 x1 和目标序列的第一个单词 x2

下面举一个例子：

encoder的输入: i love you

decoder的输入: /f 我爱你

此时的 decoder 是由4个词组成的向量，Mask 是一个 4*4 大小的矩阵

当 decoder 预测第一个单词 '我' 时, decoder 的输入是一个特殊字符 '/f'，mask为[1,0,0,0]

当 decoder 预测第二个单词 '爱' 时, decoder 的输入是一个特殊字符 '/f' 和第一个单词 '我'，mask为[1,1,0,0]

代码如下：


   
   
     
     
      
      
     
     
     
     
      
      
       
       import torch
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       from torch.nn 
       
       import functional 
       
       as F
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       #（1）构建下三角形状的mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 目标序列中有两个句子，分别包含3、4个单词
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tgt_len = torch.Tensor([
       
       3,
       
       4]).to(torch.int32)  
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 目标序列有效单词矩阵 shape=[3,3], shape=[4,4]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tgt_matrix = [torch.ones(L, L) 
       
       for L 
       
       in tgt_len]  
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 对每个元素全为1句子矩阵构造一个下三角矩阵
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tri_matrix = [torch.tril(mat) 
       
       for mat 
       
       in tgt_matrix]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 第一个句子长度为3，生成3*3大小且下三角区域的元素权威1，其余全为0的矩阵
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(tri_matrix)  
       
       # 每个mask的shape=[seq_len,seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 构建有效单词的矩阵，通过padding将每个句子的矩阵大小调整成一样的
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       new_tri_matrix = []  
       
       # 保存padding后mask矩阵
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       for seq_len, matrix 
       
       in 
       
       zip(tgt_len, tri_matrix):  
       
       # 遍历每个下三角矩阵mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           matrix = F.pad(matrix, pad=(
       
       0,
       
       max(tgt_len)-seq_len,
       
       0,
       
       max(tgt_len)-seq_len))  
       
       # 在矩阵的下方和右侧padding成相同相撞
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           matrix = torch.unsqueeze(matrix, dim=
       
       0)  
       
       # 维度扩充[seq_len,seq_len]==>[1,seq_len,seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           new_tri_matrix.append(matrix)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 将列表类型变成tensor, 其中值为0对应的元素代表需要mask掉
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_tri_matrix = torch.cat(new_tri_matrix, dim=
       
       0)
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       '有效下三角矩阵mask:', valid_tri_matrix)  
       
       # shape=[2,4,4]
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 将需要mask的元素用布尔类型表示，True代表需要mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       invalid_tri_matrix = (
       
       1 - valid_tri_matrix).to(torch.
       
       bool)
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       '布尔mask:', invalid_tri_matrix)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       #（2）对decoder的输入张量做mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 随机初始化一个 Q @ K^T 的计算结果 [batch, tgt_seq_len, tgt_seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       score = torch.randn(
       
       2, 
       
       max(tgt_len), 
       
       max(tgt_len))
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 将mask中True元素对应score中的值变成非常小的值
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       masked_score = score.masked_fill(invalid_tri_matrix, value=-
       
       1e10)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 将mask后的结果经过softmax，得到注意力矩阵
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       softmax_score = F.softmax(masked_score, dim=-
       
       1)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       '原始输入:', score)
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       'mask后的输入:', masked_score)

然后构造一个 decoder 的输入 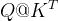Q@K^T ，它的 shape=[batch, seq_len, seq_len]，如下面的第三个矩阵。

将输入张量 score 中与 mask 中True元素对应的位置变成一个非常小的数，如下面的第四个矩阵。


   
   
     
     
      
      
     
     
     
     
      
      
       
       # 有效下三角矩阵mask: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[
       
       1., 
       
       0., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       0., 
       
       0., 
       
       0., 
       
       0.]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[
       
       1., 
       
       0., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       1.]]])
      
      
     
     

     
     
      
      
     
     
     
     
      
          
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 布尔mask: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[
       
       False,  
       
       True,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       True,  
       
       True,  
       
       True,  
       
       True]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[
       
       False,  
       
       True,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False, 
       
       False]]])
      
      
     
     

     
     
      
      
     
     
     
     
      
          
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 原始输入scorce: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[ 
       
       0.5266, -
       
       0.7873, -
       
       0.2481,  
       
       0.5554],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.3146,  
       
       0.1668, -
       
       1.6488, -
       
       0.5159],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       0.1590, -
       
       2.1458,  
       
       0.0217,  
       
       0.4044],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       1.0169,  
       
       0.8640, -
       
       0.9029,  
       
       0.5957]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[-
       
       0.6277,  
       
       0.0611, -
       
       1.3732, -
       
       0.6897],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.3523,  
       
       0.6712,  
       
       0.0491,  
       
       2.2301],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       0.4627,  
       
       0.1737,  
       
       1.0111, -
       
       1.4099],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       0.1994,  
       
       0.2538,  
       
       0.5689, -
       
       0.2558]]])
      
      
     
     

     
     
      
      
     
     
     
     
      
          
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # mask后的输入: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[ 
       
       5.2655e-01, -
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.3146e+00,  
       
       1.6676e-01, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.5899e-01, -
       
       2.1458e+00,  
       
       2.1674e-02, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[-
       
       6.2770e-01, -
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.3523e+00,  
       
       6.7119e-01, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       4.6272e-01,  
       
       1.7366e-01,  
       
       1.0111e+00, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       1.9943e-01,  
       
       2.5381e-01,  
       
       5.6886e-01, -
       
       2.5576e-01]]])

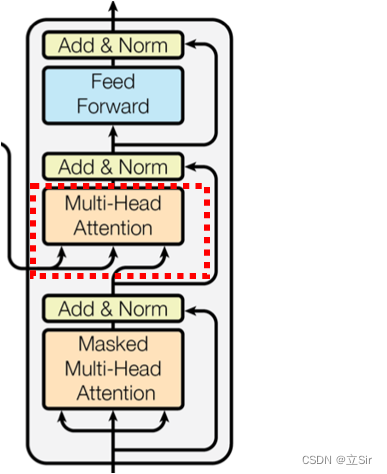
2. Decoder 中特征序列和目标序列之间的 Mask

该部分的 mask 代码对应结构图中的区域如下。这部分的 mask 涉及到目标序列和特征序列，在计算 self-attention 时，是目标序列的 query 和特征序列的 key、value 做计算。其中 key 和 value 是 Encoder 的输出，query 是上一个 DecoderBlock 的输出。

首先分别构造一个特征序列和一个目标序列，特征序列中第一句话有2个单词，第二句话有4个单词；目标序列中的第一句话有3个单词，第二句话有5个单词。

接下来就需要把特征序列和目标序列的长度各自给统一起来，将特征序列的所有句子都填充成4个单词，目标序列的所有句子都填充成5个单词。有效单词区域的元素用 1 来表示，padding 的元素用 0 来表示。

代码如下：


   
   
     
     
      
      
     
     
     
     
      
      
       
       # Decoder部分的目标序列对特征序列的muti-head-attention中的mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 目标序列和特征序列之间的长度不一样，需要将原序列中和目标序列中padding后的元素mask掉
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       import torch 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       from torch 
       
       import nn
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       from torch.nn 
       
       import functional 
       
       as F
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       #（1）构造序列
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       src_len = torch.Tensor([
       
       2,
       
       4]).to(torch.int32)  
       
       # 特征序列中有两个句子，分别包含2、4个单词
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tgt_len = torch.Tensor([
       
       3,
       
       5]).to(torch.int32)  
       
       # 目标序列中有两个句子，分别包含3、5个单词
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 对序列编码，有效单词位置的元素为1
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_src_pos = [torch.ones(L) 
       
       for L 
       
       in src_len]  
       
       # 特征序列 [tensor([1., 1.]), tensor([1., 1., 1., 1.])]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_tgt_pos = [torch.ones(L) 
       
       for L 
       
       in tgt_len]  
       
       # 目标序列 [tensor([1., 1., 1.]), tensor([1., 1., 1., 1., 1.])]
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 在计算时需要保证特征序列的长度和目标序列的长度一致，因此将每句话的单词数padding成相同长度
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       max_src_len = 
       
       max(src_len)  
       
       # 将特征序列的单词数统一成4个
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       max_tgt_len = 
       
       max(tgt_len)  
       
       # 将目标序列的单词数统一成5个
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       new_valid_pos = []  
       
       # 保存padding后的特征序列和目标序列
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       for sent 
       
       in valid_src_pos:  
       
       # 遍历每个特征句子
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           sent = F.pad(sent, pad=(
       
       0, max_src_len - 
       
       len(sent)))  
       
       # 将每句话的长度填充到4
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           sent = torch.unsqueeze(sent, dim=
       
       0)  
       
       # 维度扩充 [max_src_len]==>[1, max_src_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           new_valid_pos.append(sent)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       for sent 
       
       in valid_tgt_pos:  
       
       # 遍历每个目标句子
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           sent = F.pad(sent, pad=(
       
       0, max_tgt_len - 
       
       len(sent)))  
       
       # 将每句话的长度填充到5
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           sent = torch.unsqueeze(sent, dim=
       
       0)  
       
       # 维度扩充 [max_tgt_len]==>[1, max_tgt_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
           new_valid_pos.append(sent)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 前两个句子属于特征序列，后两个句子属于目标序列。将列表类型在axis=0维度上堆叠
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_src_pos = torch.cat(new_valid_pos[:
       
       2], dim=
       
       0)  
       
       # tensor([[1., 1., 0., 0.], [1., 1., 1., 1.]])
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_tgt_pos = torch.cat(new_valid_pos[
       
       2:], dim=
       
       0)  
       
       # tensor([[1., 1., 1., 0., 0.], [1., 1., 1., 1., 1.]])
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       #（2）构造mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # Q @ K^T 的shape为 [batch, tgt_seq_len, src_seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 因此mask的shape也为 [batch, tgt_seq_len, src_seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 有效特征序列[2,4]==>[2,4,1], 有效目标序列[2,5]==>[2,5,1]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_src_pos = torch.unsqueeze(valid_src_pos, dim=-
       
       1)  
       
       # 值为1的元素代表有效单词，值为0的元素代表padding后的区域
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_tgt_pos = torch.unsqueeze(valid_tgt_pos, dim=-
       
       1)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 计算目标序列对特征序列有效性关系的矩阵，元素为0代表是padding后的单词
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # [b, tgt_seq_len, 1] @ [b, 1, src_seq_len] = [b, tgt_seq_len, src_seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       valid_cross_pos_matrix = torch.bmm(valid_tgt_pos, valid_src_pos.transpose(
       
       1,
       
       2))
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       '有效关系矩阵：', valid_cross_pos_matrix)  
       
       # torch.Size([2, 5, 4])
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 得到无效矩阵，1代表需要mask的元素，变成布尔类型，True代表需要mask的元素
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       invalid_cross_pos_matrix = 
       
       1 - valid_cross_pos_matrix
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       invalid_cross_pos_matrix = invalid_cross_pos_matrix.to(torch.
       
       bool)
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       'mask矩阵:', invalid_cross_pos_matrix)  
       
       # torch.Size([2, 5, 4])
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       #（3）对输入张量做mask
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # ------------------------------------------------------ #
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 随机初始化一个 Q @ K^T 的计算结果 [batch, tgt_seq_len, src_seq_len]
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       score = torch.randn(
       
       2, 
       
       5, 
       
       4)
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # mask中True元素对应的score中的元素值变成一个非常小的数
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       masked_score = torch.masked_fill(score, mask=invalid_cross_pos_matrix, value=-
       
       1e10)
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       '原输入:', score)
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       print(
       
       '打上mask后的输入:', masked_score)

接下来构造 mask，它的 shape 是和 Q@K^T 计算后的矩阵的 shape 相同，即 [batch, tgt_seq_len, src_seq_len]，其中 tgt_seq_len 代表目标序列中每个句子包含多少个单词，src_seq_len 代表特征序列中每个句子包含多少个单词。

下面的第一个矩阵代表对目标序列和特征序列计算关系矩阵，元素为1代表有效单词，0 代表是经过padding 后得到的单词。

之后计算一个无效区域矩阵，将所有 padding 得到的单词区域像素值变成 True，代表需要将这个元素 mask 掉。如下面的第二个矩阵。

然后构造一个和 self-attention 中 Q@K^T 计算结果 shape 相同的输入 source，如下面的第三个矩阵。

然后对输入 source 添加 mask，将 mask 中元素 True 对应的 source 元素变成一个非常小的值，这样在梯度反向传播过程中 padding 的元素梯度更新非常小，降低 padding 区域对有效单词区域的影响。如下面的第四个矩阵。


   
   
     
     
      
      
     
     
     
     
      
      
       
       # 有效关系矩阵： 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[
       
       1., 
       
       1., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       0., 
       
       0., 
       
       0., 
       
       0.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       0., 
       
       0., 
       
       0., 
       
       0.]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[
       
       1., 
       
       1., 
       
       1., 
       
       1.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       1.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       1.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       1.],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       1., 
       
       1., 
       
       1., 
       
       1.]]])
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # mask矩阵: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[
       
       False, 
       
       False,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       True,  
       
       True,  
       
       True,  
       
       True],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       True,  
       
       True,  
       
       True,  
       
       True]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[
       
       False, 
       
       False, 
       
       False, 
       
       False],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False, 
       
       False],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False, 
       
       False],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False, 
       
       False],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [
       
       False, 
       
       False, 
       
       False, 
       
       False]]])        
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 原输入: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[ 
       
       1.4030, -
       
       0.0176, -
       
       2.9678, -
       
       0.5551],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       2.6138, -
       
       0.8088,  
       
       0.6641, -
       
       0.0128],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       0.0370, -
       
       0.3206, -
       
       0.6634,  
       
       0.3626],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       1.1978,  
       
       1.9831, -
       
       0.3541, -
       
       0.8766],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       0.0655,  
       
       0.4267, -
       
       0.3459,  
       
       1.8217]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[-
       
       0.2351, -
       
       1.3515,  
       
       0.4783, -
       
       0.9379],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       0.2302, -
       
       1.5482, -
       
       0.0825,  
       
       1.0711],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       0.3793, -
       
       0.9595,  
       
       0.9457, -
       
       1.5746],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       0.3685,  
       
       1.1116, -
       
       2.3528, -
       
       0.3916],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.2416,  
       
       0.9410, -
       
       0.5407,  
       
       0.8035]]])
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       # 打上mask后的输入: 
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
       tensor([[[ 
       
       1.4030e+00, -
       
       1.7624e-02, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       2.6138e+00, -
       
       8.0884e-01, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       3.7038e-02, -
       
       3.2057e-01, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10, -
       
       1.0000e+10]],
      
      
     
     

     
     
      
      
     
     
     
     
      
       
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
               [[-
       
       2.3507e-01, -
       
       1.3515e+00,  
       
       4.7825e-01, -
       
       9.3789e-01],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       2.3023e-01, -
       
       1.5482e+00, -
       
       8.2474e-02,  
       
       1.0711e+00],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       3.7931e-01, -
       
       9.5949e-01,  
       
       9.4568e-01, -
       
       1.5746e+00],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [ 
       
       3.6855e-01,  
       
       1.1116e+00, -
       
       2.3528e+00, -
       
       3.9157e-01],
      
      
     
     

     
     
      
      
     
     
     
     
      
      
       
                [-
       
       1.2416e+00,  
       
       9.4099e-01, -
       
       5.4066e-01,  
       
       8.0347e-01]]])