前言
何为前缀?已知一个一维数组a[n] , 那么对应数组s[n],s[ i ] = a [1]+a[2] +…+a[ i ]。那么s即为a的前缀和数组。 差分则反之,a[ i ] = s[ i ] - s [ i-1], a为s的差分数组。
提示:以下是本篇文章正文内容,下面案例可供参考
一、前缀和
前缀和的作用:对于求解数组 a 从[ l ,r] 区间的和效率可以优化,利用前缀和数组,可以让预处理时间复杂度变成O(n),查询变成O(1)。
一维前缀和问题
一维前缀和非常容易,就是创建一个 s 前缀和数组。利用 s 求所需区间的和。
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int m = s.nextInt();
int[] q = new int[n];
int[] p = new int[n+1]; //这里n+1对应题目中的第几数到第几个数的和
p[0] = 0; //而且n+1的数组大小,令p[0] = 0,方便后面运算。
for(int i = 0;i < n;i++){
q[i] = s.nextInt();
p[i + 1] = p[i] + q[i];
}
for(int i = 0;i < m;i++){
int a = s.nextInt();
int b = s.nextInt();
System.out.println(p[b] - p[a-1]);
}
}
}
二维前缀和问题
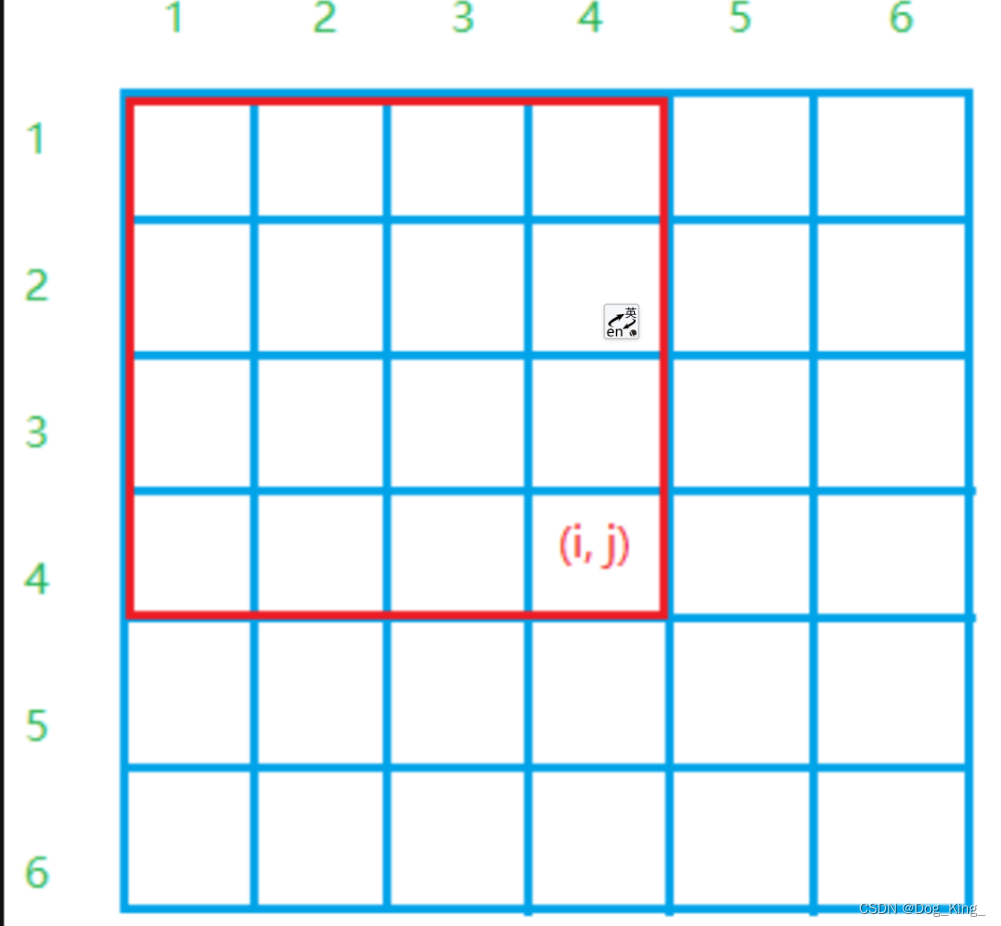
首先二维前缀和公式的成立是基于容斥定理的,二维前缀和实际上就是二维数组上的前缀和了。一维数组的前缀和也是一个一维数组,同样地,二维数组的前缀和也是一个二维的数组。s[ i ][ j ]即为 i * j 的矩阵中所有数的和。
这钟题目套下面的前缀和公式即可。
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int m = s.nextInt();
int q = s.nextInt();
int[][] a =new int[n][m];
for(int i = 0; i < n;i++){
for(int j = 0; j < m;j++)
a[i][j] = s.nextInt();
}
//求个矩阵和
int[][] b = new int[n+1][m+1];
for(int i = 0; i < n+1;i++)
b[i][0] = 0;
for(int i = 0; i < m+1;i++)
b[0][i] = 0;
for(int i = 1;i < n + 1;i++){
for(int j = 1;j < m + 1;j++)
{
b[i][j] = a[i-1][j-1] + b[i-1][j] + b[i][j-1] - b[i-1][j-1];
}
}
for(int i = 0; i < q;i++){
int x1 = s.nextInt();
int y1 = s.nextInt();
int x2 = s.nextInt();
int y2 = s.nextInt();
System.out.println(b[x2][y2] - b[x1-1][y2] - b[x2][y1-1] + b[x1-1][y1-1] );
}
}
})
二、差分
差分即为前缀和的逆运算。
差分法应用在处理区间问题时比较多。一个数列要在很多不确定的区间内加上相同的一个数,如果直接在原数列上操作是非常复杂且耗时的,差分法就是先将数列拆分,构造一个拆分的新数列,在这个新数列上进行我们想要的操作之后,在将这个数列合并起来即可。
听起来好像复杂了很多,其实不然,这样处理反而能减少很多操作,比如不用对给定区间内的原数列的每一项进行操作,只需要在新数列上操作区间左右边界的这两项即可,这样就达到了减少耗时的效果。
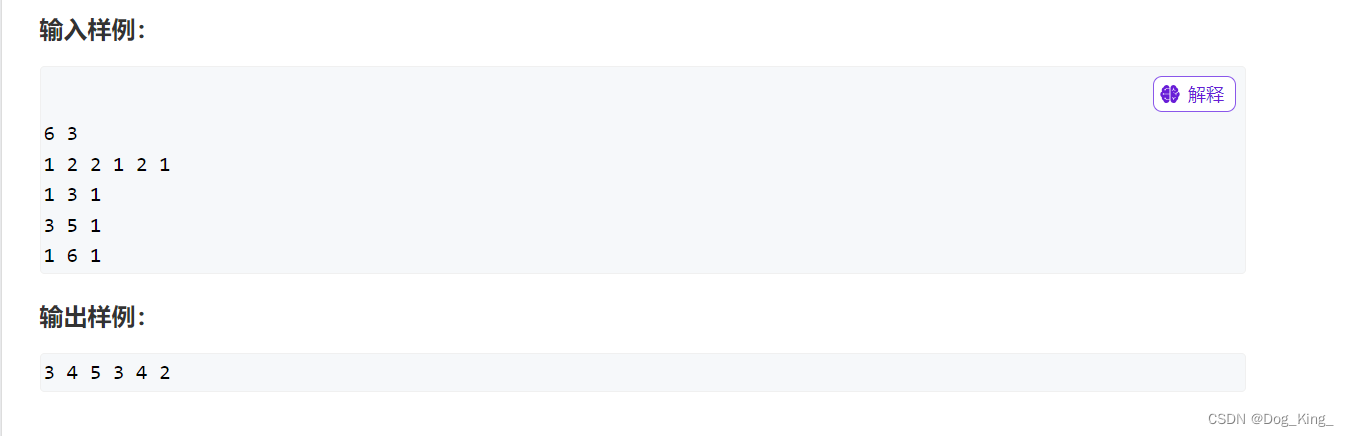
一维差分问题
如果我们采用暴力的方法就是用三个循环每个循环里面再嵌套循环,挨个加c。我们来分析一下用差分的方法好在哪里。差分可以将对a数组任意区间的同一操作优化到O(1)。
这里初始化差分数组b[n]时可以自直接做差a[ i ] - a[ i-1] = b[ i ],这样的话b和a的大小都是n + 1。更好的方法就是利用insert函数,先默认所有的a[ ]里的值都是o,然后挨个insert插入,在[i , i]的区间插入a[ i ]。
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int m = s.nextInt();
int[] a = new int[n+1];
a[0] = 0;
int[] b = new int[n+1]; //差分数组b[]
for(int i = 1;i <= n;i++)
a[i] = s.nextInt();
for(int i = 1;i < n+1;i++)
//b[i] = a[i] - a[i-1]; 差分数组初始化。
insert(b,i,i,a[i]); //利用insert方法等价于从0数组构造
//这里需要思考一下如何用到差分。
for(int i =0;i < m;i++){
int l = s.nextInt();
int r = s.nextInt();
int c = s.nextInt();
insert(b,l,r,c);
}
for(int i = 1; i < n ;i++) //O(n)的时间复杂度解决了所有问题
b[i] += b[i-1];
for(int i = 0;i < n;i++ )
System.out.print(b[i]+" ");
}
public static void insert(int[] b , int l,int r,int c ){ //核心插入
//即对a数组从l到r每个数都加c
b[l-1] += c;
b[r] -= c;
}
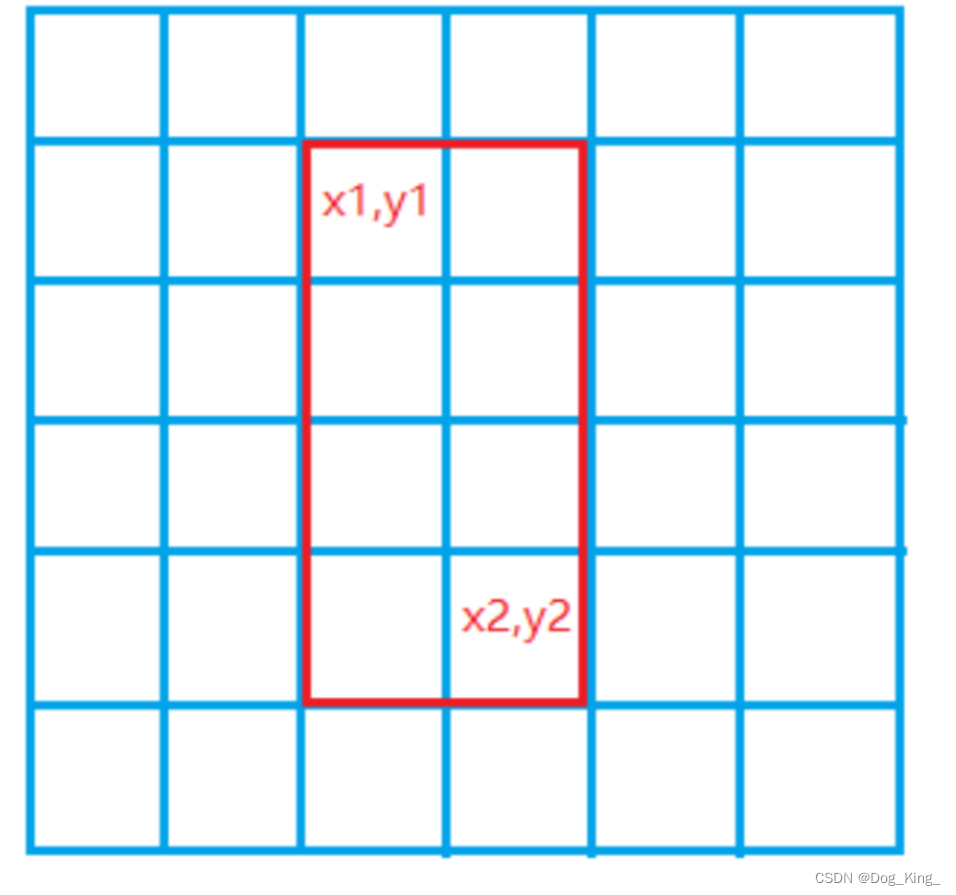
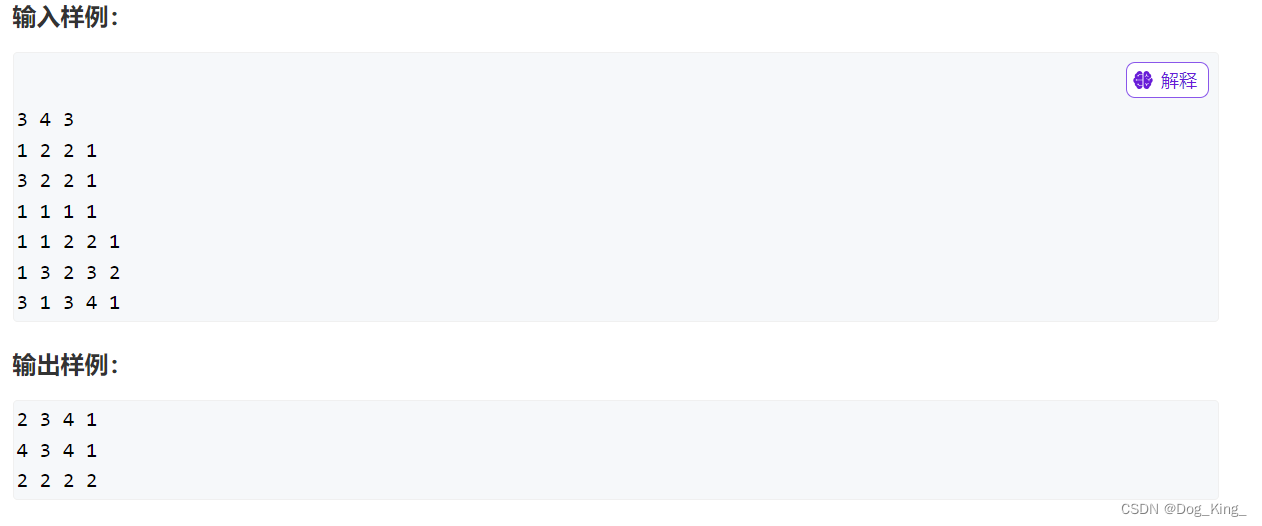
二位差分问题
其实这种题目和上面一维的一样,核心是写insert函数,insert函数写出来就会轻松地得到差分数组b[ ][ ]。
而且这里的第 i 个数对应数组下标 i-1,数组可以在 i=0或者j=0的位置不存储元素,和题目统一,可以更简洁明了。
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner s = new Scanner(System.in);
int n = s.nextInt();
int m = s.nextInt();
int q = s.nextInt();
int[][] a = new int[n][m];
int[][] b = new int[n+1][m+1]; //构造一个辅助用的差分矩阵
for(int i = 0;i < n;i++){
for(int j = 0;j < m;j++){
a[i][j] = s.nextInt();
insert(b,i,j,i,j,a[i][j]);
}
}
while(q-- > 0){
int x1 = s.nextInt();
int y1 = s.nextInt();
int x2 = s.nextInt();
int y2 = s.nextInt();
int c = s.nextInt();
insert(b,x1-1,y1-1,x2-1,y2-1,c);
}
a[0][0] = b[0][0]; //这一大块是根据b[0][0]构建最终的a[0][0]
for(int i = 1;i < n;i++)
a[i][0] = a[i-1][0] + b[i][0] ;
for(int j = 1;j < m;j++)
a[0][j] = a[0][j-1] + b[0][j];
for(int i = 1;i < n;i++){
for(int j = 1;j < m; j++){
a[i][j] = a[i-1][j] + a[i][j-1] - a[i-1][j-1] + b[i][j];
}
}
for(int i = 0;i < n;i++){
for(int j = 0;j < m; j++){
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
public static void insert(int[][] b,int x1,int y1,int x2,int y2,int c){
b[x1][y1] += c;
b[x2 + 1][y1] -=c;
b[x1][y2+1] -=c;
b[x2+1][y2+1] +=c;
}
}