1.SVM作用

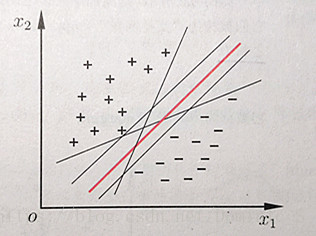
对于给定的训练样本集D={(x1,y1), (x2,y2),… (xn,yn)}，yi属于{-1，+1}，希望能找出一个超平面，把不同类别的数据集分开，对于线性可分的数据集来说，这样的超平面有无穷多个，而最优的超平面即是分隔间距最大的中间那个超平面

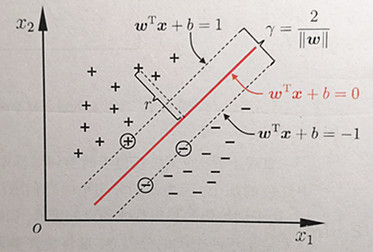
2.硬间隔最大化

对于以上的KKT条件可以看出，对于任意的训练样本总有ai=0或者yif(xi) - 1=0即yif(xi) = 1
1）当ai=0时，代入最终的模型可得：f(x)=b，即所有的样本对模型没有贡献
2）当ai>=0，则必有yif(xi) = 1，注意这个表达式，代表的是所对应的样本刚好位于最大间隔边界上，是一个支持向量，这就引出一个SVM的重要性质：训练完成后，大部分的训练样本都不需要保留，最终的模型仅与支持向量有关。

关于对偶问题

• 转化为对偶问题，具体就是把所有的约束条件，分别乘上拉格朗日乘子ai>=0，添加到需要优化的目标函数里，形成一个待优化的表达式
• 为什么原问题能求解，却要转化为对偶问题？
  1）带约束的原问题求解比较困难，变成对偶问题可以把约束条件和待优化的目标融合在一个表达式里面
  2）拉格朗日对偶问题一般是凹函数（求最大值），即使原问题是非凸的，变成对偶问题更容易优化求解
  3）对偶问题能自然的引入核技巧，方便后续用来解决低维线性不可分的问题

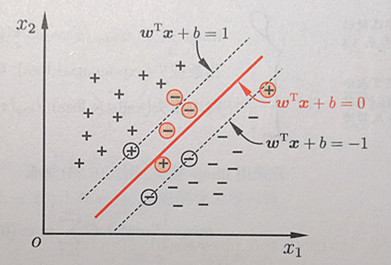
3.软间隔最大化

前面我们是假定所有的训练样本在样本空间或特征空间中是严格线性可分的，即存在一个超平面能把不同类的样本完全分开，然鹅现实任务中很难确定这样的超平面（不管是线性超平面还是经过核变换到高维空间的超平面），所以引入松弛变量，允许一些样本出错，但我们希望出错的样本越少越好，所以松弛变量也有限制（注：公式中的松弛变量不是单单一个数，每个样本都有对应的松弛变量）。引入松弛变量的间隔问题成为软间隔

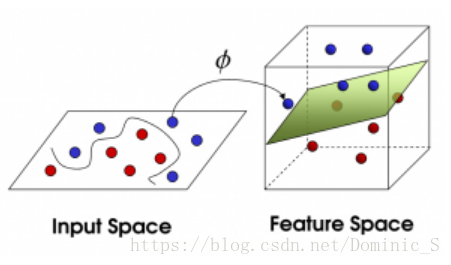
4.核函数

前面我们都是假设样本是线性可分的，虽然软间隔不完全可分，但大部分还是可分的。而现实任务中很可能遇到这样的情况，即不存在一个能够正确划分两个类别样本的超平面，对这样的问题，可以将样本从原始空间映射到一个更高维的特征空间中，使得样本在这个特征空间中线性可分。数学上可以证明，如果原始空间是有限维，即属性数有限，则一定存在一个高维特征空间使样本可分。

参考文章：《机器学习》——周志华