KMP

KMP算法是一个效率高的字符串匹配算法。一般比较两个串的时间复杂度是两个字符串长度之积，效率并不是很高，而KMP的时间复杂度是两个字符串长度之和。
比如给你两个字符串，主串是：abbadabbc，模式串 abbcdabb KMP好处在于能够使模式串尽可能地往后面移动，主串匹配地位置不用重复去匹配，借助 Next[]数组，但是数组命名不能是 next，否则 oj 提交会报错
KMP核心思想: 尽可能地将模式串向后移动，减少匹配时间
例如模式串 abbcdabba，发现 abb 有重复地位置，那么直接将模式串首位置移动到后面部分地首位置即可。
求Next[]
后缀:从某个位置开始到末尾的一个子串。
前缀:从首部开始到任意位置。
就是一个模式串自匹配地过程，以 abbcdabb 为例

模式串自匹配，求 Next[]

void Get_next(int p[],int n)
{
    ne[0]=ne[1]=0;
    for(int i=1;i<= n;++i)  //自匹配
    {
        int j=ne[i];
        while(j&&p[i]!=p[j]) j=ne[j];   //匹配失败，返回当前后缀的前缀
        ne[i+1]=(p[i]==p[j])?j+1:0;
    }
    // for(int i=1;i<=n;++i) printf("ne[%d]=%d  ",i,ne[i]);puts("");
}

Kmp 主串与子串匹配

void Kmp(int s[],int ls,int p[],int lp)  //s:主串 p:子串，询问 p 是否包含于 s
{
    int last=-1;
    Get_next(p,lp);    //求 next[] 数组
    for(int i=0,j=0;i<ls;i++)
    {
        while(j&&s[i]!=p[j]) j=ne[j];
        if(s[i]==p[j]) j++;
        if(j==lp) {    //匹配成功
            last = i+2-j;
              printf("%d\n",last);
        return;
        }
    }
    puts("-1");
    return;
}

题目集

亲和串

亲和串

题目大意
人随着岁数的增长是越大越聪明还是越大越笨，这是一个值得全世界科学家思考的问题,同样的问题Eddy也一直在思考，因为他在很小的时候就知道亲和串如何判断了，但是发现，现在长大了却不知道怎么去判断亲和串了，于是他只好又再一次来请教聪明且乐于助人的你来解决这个问题。
亲和串的定义是这样的：给定两个字符串s1和s2,如果能通过s1循环移位，使s2包含在s1中，那么我们就说s2 是s1的亲和串。
Input
本题有多组测试数据，每组数据的第一行包含输入字符串s1,第二行包含输入字符串s2，s1与s2的长度均小于100000。
Output
如果s2是s1的亲和串，则输出"yes"，反之，输出"no"。每组测试的输出占一行。
样例输入

AABCD
CDAA
ASD
ASDF

样例输出

yes
no

#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1e5+7;
char s[maxn<<1],t[maxn];
int ne[maxn];
void Get_next(char p[],int n)
{
    ne[0]=ne[1]=0;
    for(int i=1;i<= n;++i)  //自匹配
    {
        int j=ne[i];
        while(j&&p[i]!=p[j]) j=ne[j];   //匹配失败，返回当前后缀的前缀
        ne[i+1]=(p[i]==p[j])?j+1:0;
    }
}
void Kmp(char s[],int ls,char p[],int lp)  //s:主串 p:子串，询问 p 是否包含于 s
{
    Get_next(p,lp);    //求 next[] 数组
    for(int i=0,j=0;i<ls;i++)
    {
        while(j&&s[i]!=p[j]) j=ne[j];
        if(s[i]==p[j]) j++;
        if(j==lp) {    //匹配成功
            puts("yes");
            return;
        }
    }
    puts("no");
    return;
}
int main()
{
    while(~scanf(" %s %s",s,t))
    {
        memset(ne,0,sizeof ne);
        int ls=strlen(s),lt=strlen(t);
        int idx=ls;
        if(ls<lt)
            while(ls<lt){
                for(int i=1;i<=ls;++i) s[idx++]=s[i];
                ls=idx;
            }

        for(int i=0;i<ls;++i) s[idx++]=s[i];
 
        Kmp(s,idx,t,lt);
    }
    return 0;
}

Period

Period

题目大意
给你一个 n 和一个长度为 n 的字符串，让你求找这个字符串中的子串重复出现的次数及其长度，长度是重复出现多少次数的整个长度。
输入格式
输入有多组数据，输入一个 n 和 字符串 s，当 n == 0 时输入结束。
输出格式
输出Test case #,第几组数据，下面输出符合的数据，循环子串长度和循环次数，每组数据占一行。每个Test之间有个换行
样例输入

3
aaa
12
aabaabaabaab
0

样例输出

Test case #1
2 2
3 3

Test case #2
2 2
6 2
9 3
12 4

#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1e6+7;
char s[maxn];
int ne[maxn];
void Get_next(char p[],int n)
{
    ne[0]=ne[1]=0;
    for(int i=1;i<=n;++i)  //自匹配
    {
        int j=ne[i];
        while(j&&p[i]!=p[j]) j=ne[j];   //匹配失败，返回当前后缀的前缀
        ne[i+1]=(p[i]==p[j])?j+1:0;
    }
}
int main()
{
    int n,cnt=0;
    while(~scanf("%d",&n)&&n)
    {
        memset(ne,0,sizeof ne);
        scanf("%s",s);
        Get_next(s,n);
        printf("Test case #%d\n",++cnt);
        for(int i=2;i<=n;++i)
        {
            int l=i-ne[i];
            if(!(i%l)&&ne[i]) printf("%d %d\n",i,i/l);
        }
        printf("\n");
    }
    return 0;
}

Number Sequence

Number Sequence

题目大意
给你一个数组a 和 b ，问 b 是不是 a 的子集。
输入格式
输入一个T，代表有 T 组测试。
输入一个$N$ 和$M$ (1 $\le$ $M$ $\le$ 10000, 1 $\le$ $N$ $\le$ 1000000),输入N 个数，表示 a[] 数组，输入 M 个数，表示 b 数组，如果满足题意输出第一次出现的最初位置，如果不满足题意输出 -1。
样例输入

2
13 5
1 2 1 2 3 1 2 3 1 3 2 1 2
1 2 3 1 3
13 5
1 2 1 2 3 1 2 3 1 3 2 1 2
1 2 3 2 1

样例输出

6
-1

#include <cstdio>
#include <cstring>
using namespace std;
const int maxn=1e6+7;
int s[maxn],t[maxn];
int ne[maxn];
void Get_next(int p[],int n)
{
    ne[0]=ne[1]=0;
    for(int i=1;i<= n;++i)  //自匹配
    {
        int j=ne[i];
        while(j&&p[i]!=p[j]) j=ne[j];   //匹配失败，返回当前后缀的前缀
        ne[i+1]=(p[i]==p[j])?j+1:0;
    }
}
void Kmp(int s[],int ls,int p[],int lp)  //s:主串 p:子串，询问 p 是否包含于 s
{
    int last=-1;
    Get_next(p,lp);    //求 next[] 数组
    for(int i=0,j=0;i<ls;i++)
    {
        while(j&&s[i]!=p[j]) j=ne[j];
        if(s[i]==p[j]) j++;
        if(j==lp) {    //匹配成功
            last = i+2-j;
              printf("%d\n",last);
        return;
        }
    }
    puts("-1");
    return;
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        int x,y;
        scanf(" %d%d",&x,&y);
        for(int i=0;i<x;++i) scanf("%d",&s[i]);
        for(int i=0;i<y;++i) scanf("%d",&t[i]);
        Kmp(s,x,t,y);
    }
    return 0;
}

Trie 树

Trie树:高效的存储和查找字符串集合的数据结构
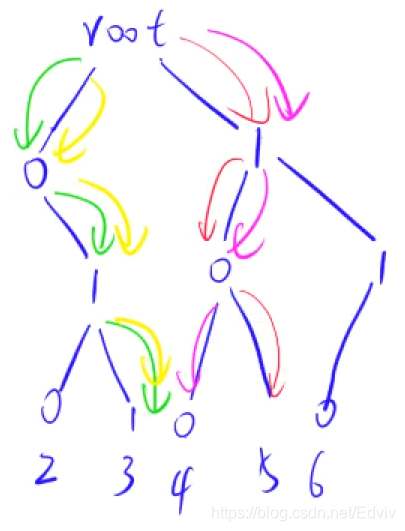
串a:010 串b:011 串c:100 串d:101 串e:110构造出来的树如下图所示:

Trie树基本性质:根结点不包含任何字符，除根结点外的每个子结点都包含一个字符；从根节点到某一个结点，路径上经过的字符连接起来，为该结点对应的字符串；每个结点的所有子结点包含的字符互不相同。
Trie树的建立

int son[maxn][26], cnt[maxn], idx;
 //下标是 0 的点既是根节点, 又是空节点
// cnt[]:存储以当前这个点结尾的点有多少个,
//  idx: 存储当前用到了哪个下标
void insert(char str[])
{
    int p = 0;   //根节点开始
    for(int i = 0; str[i] ;i++)  //从前往后遍历，字符串结尾 \0
    {
        int u = str[i] - 'a';    //小写字母 a~z 映射成 0~25
        if(!son[p][u]) son[p][u] = ++idx;  //当前这个点的儿子不存在，我们就创建出来
        p = son[p][u];   //把值存入创建的节点
        /***
        cnt[p]++;  //前缀相同的单词数量
        ***/
    }
    cnt[p] ++;  // 以这个单词结尾的数量多了一个
}

Trie树的查询

int query(char str[])
{
    int p = 0;
    for(int i = 0; str[i]; i++)
    {
        int u = str[i] - 'a';
        if(!son[p][u]) return 0;  // 不存在子节点，说明该单词不存在
        p = son[p][u];
    }
    return cnt[p];  //返回以 p 结尾的单词数量
}

Trie字符串统计

题目大意
维护一个字符串集合，支持两种操作：
1.“I x”向集合中插入一个字符串x；
2.“Q x”询问一个字符串在集合中出现了多少次。
共有N个操作，输入的字符串总长度不超过 10${}^5$，字符串仅包含小写英文字母。
输入格式
第一行包含整数N，表示操作数。
接下来N行，每行包含一个操作指令，指令为”I x”或”Q x”中的一种。
输出格式
对于每个询问指令”Q x”，都要输出一个整数作为结果，表示x在集合中出现的次数。
每个结果占一行。
数据范围：1≤N≤$2\ast 10^4$
输入样例

5
I abc
Q abc
Q ab
I ab
Q ab

输出样例

1
0
1

#include <cstdio>
using namespace std;
const int maxn=2e4+7;
char s[maxn],op;
int son[maxn<<4][26],cnt[maxn],idx;
void insert(char s[])
{
    int p=0,i=0;
    while(s[i])
    {
        int u=s[i]-'a';
        if(!son[p][u]) son[p][u]=++idx;
        p=son[p][u];
        i++;
    }
    cnt[p]++;
}
int find(char s[])
{
    int p=0,i=0;
    while(s[i])
    {
        int u=s[i]-'a';
        if(!son[p][u]) return 0;
        p=son[p][u];
        i++;
    }
    return cnt[p];
}
int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        scanf(" %c%s",&op,s);
        if(op=='I') insert(s);
        else printf("%d\n",find(s));
    }
    return 0;
}

最大异或对

题目描述
在给定的 $N$ 个整数, $A_1$，$A_2$……$A_N$ 中选出两个进行xor（异或）运算，得到的结果最大是多少？
输入格式
第一行输入一个整数N。
第二行输入N个整数$A_1$～$A_N$。
输出格式
输出一个整数表示答案。
数据范围 1$\le$ $N$ $\le$ 10${}^5$, 0≤$A_i$<2${}^{31}$
输入样例

3
1 2 3

输出样例

3

#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn=1e5+7;
int a[maxn],son[maxn<<4][2],idx;
void insert(int x)
{
    int p=0;
    for(int i=30;~i;--i)
    {
        int &s=son[p][x>>i&1];
        if(!s) s=++idx;  //创建信节点
        p=s;
    }
}
int find(int x)
{
    int ans=0,p=0;
    for(int i=30;~i;--i)
    {
        int t=x>>i&1;  //第 i 位 是 0 还是 1
        if(son[p][!t])
        {
            ans+=1<<i;
            p=son[p][!t];
        }
        else p=son[p][t];
    }
    return ans;
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;++i)
    {
        scanf("%d",&a[i]);
        insert(a[i]);
    }
    int res=0;
    for(int i=0;i<n;++i) res=max(res,find(a[i]));
    printf("%d\n",res);
    return 0;
}

AC自动机

AC自动机：Aho-Corasickautomation，该算法在1975年产生于贝尔实验室，是著名的多模匹配算法之一。一个常见的例子就是给出n个单词，再给出一段包含m个字符的文章，让你找出有多少个单词在文章里出现过。

AC自动机算法分为3步：构造一棵Trie树，构造失败指针和模式匹配过程。
简单来说，AC自动机是用来进行多模式匹配（单个主串，多个模式串）的高效算法。

Next[i]:在字符串 str[i] 中，以str[i] 结尾的后缀，能够匹配的从 1 开始的非平凡(不能是原串)的前缀的最大长度。

失败指针fail:匹配时如果当前字符匹配失败，利用 fail 指针进行跳转。fail 指针指向与当前节点相同的节点，且该节点对应的后缀为当前结点能匹配的最长后缀，如果没有则指向根结点。

nt son[maxn][26],val[maxn];
int fail[maxn],last[maxn];
int size;
void clear()
{
    memset(son[0],0,sizeof(son[0]));size=1;
}
void clear_p(int x)
{
    memset(son[x],0,sizeof(son[x]));
    val[x]=0;
}

加入字符串方法与 Trie 相同

void insert(char s[])
{
    int p=0;
    for(int i=0; s[i]; i++)
    {
        int u=s[i]-'a';
        if(!son[p][u])
        {
            clear_p(size);
            son[p][u]=size++;
        }
        p=son[p][u];
    }
    val[p]++;  //以这个单词结尾的数量多了一个
}

处理 fail,last 指针
这里的 fail 与 KMP 中的 next 十分相似，都是在失配的时候利用之前的信息
达到快速匹配的目的。
last 主要用于处理字符串包含的情况

void getfail()
{
    queue<int>q;
    fail[0]=0;
    int u=0;
    for(int i=0;i<26;i++)
    {
        u=son[0][i];
        if(u)
        {
            fail[u]=0;
            last[u]=0;
            q.push(u);
        }
    }
    while(!q.empty())
    {
        int r=q.front();
        q.pop();
        for(int i=0;i<26;i++)
        {
            u=son[r][i];
            if(!u)
            {
                son[r][i]=son[fail[r]][i];
                continue;
            }
            q.push(u);
            int v=fail[r];
            while(v&&!son[v][i]) v=fail[v];
            fail[u]=son[v][i];
            last[u]=val[fail[u]]?fail[u]:last[fail[u]];
        }
    }
}

查找字符串的匹配情况

int find(char s[])
{
    int u=0,cnt=0;
    int len=strlen(s);
    for(int i=0;i<len;i++)
    {
        int c=s[i]-'a';
        u=son[u][c];
        int temp=0;
        if(val[u]) temp=u;
        else if(last[u]) temp=last[u];
        while(temp)
        {
            cnt+=val[temp];
            val[temp]=0;   //如果不清0，那么就会查询key 在 某个串中出现的次数
            temp=last[temp];
        }
    }
    return cnt;
}

Keywords Search

Keywords Search
题目大意
给定 $n$ 个长度不超过 50 的由小写英文字母组成的单词，以及一篇长为 $m$ 的文章。请问，有多少个单词在文章中出现了。
输入格式
第一行包含整数 T，表示共有 T 组测试数据。
对于每组数据，第一行一个整数 $n$，接下去 $n$ 行表示 $n$ 个单词，最后一行输入一个字符串，表示文章。
输出格式
对于每组数据，输出一个占一行的整数，表示有多少个单词在文章中出现。
数据范围：1≤n≤10${}^4$,1≤m≤$10^6$
输入样例

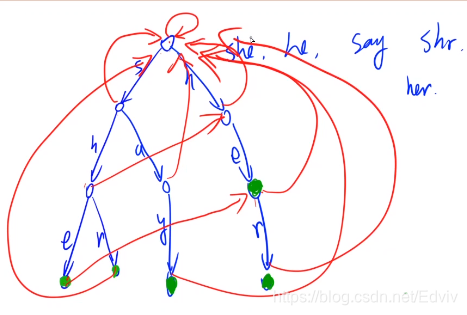
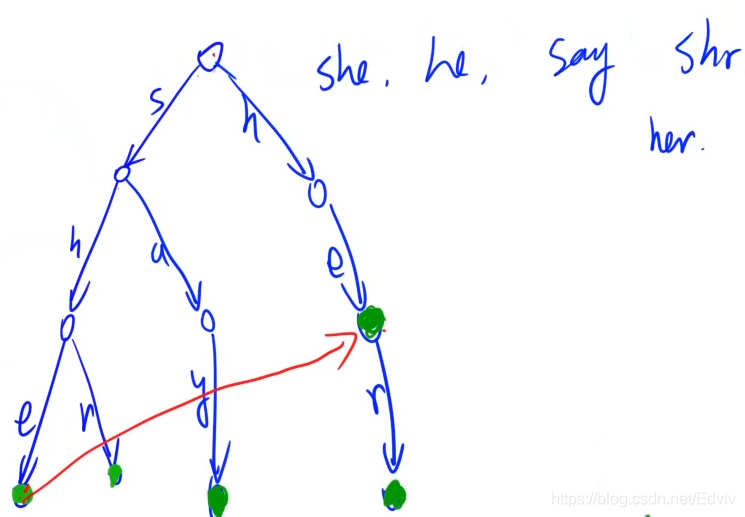
1
5
she
he
say
shr
her
yasherhs

输出样例

3

数组简化版本

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 10010, S = 55, M = 1000010;
int n;
int tr[N * S][26], cnt[N * S], idx;
char str[M];
int q[N * S], ne[N * S];
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++ idx;
        p = tr[p][t];
    }
    cnt[p] ++ ;
}
void build()
{
    queue<int>que;
    for (int i = 0; i < 26; i ++ )
        if (tr[0][i])
            que.push(tr[0][i]);
    while (!que.empty())
    {
        int t = que.front();
        que.pop();
        for (int i = 0; i < 26; i ++ )
        {
            int p = tr[t][i];
            if (!p) tr[t][i] = tr[ne[t]][i];
            else
            {
                ne[p] = tr[ne[t]][i];
                que.push(p);
            }
        }
    }
}
void find(char *str)
{
    int res = 0;
    for (int i = 0, j = 0; str[i]; i ++ )
    {
        int t = str[i] - 'a';
        j = tr[j][t];      
        int p = j;
        while (p)
        {
            res += cnt[p];
            cnt[p] = 0;
            p = ne[p];
        }
    }
    printf("%d\n", res);
}
int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;

        scanf("%d", &n);
        for (int i = 0; i < n; i ++ )
        {
            scanf("%s", str);
            insert(str);
        }
        build();
        scanf("%s", str);
        find(str);
    }
    return 0;
}

STL版本

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
using namespace std;
const int N = 10010, S = 55, M = 1000010;
int n;
int tr[N * S][26], cnt[N * S], idx;
char str[M];
int q[N * S], ne[N * S];
//构建与Trie树相同
void insert(char *str)
{
    int p = 0;
    for (int i = 0; str[i]; i ++ )
    {
        int t = str[i] - 'a';
        if (!tr[p][t]) tr[p][t] = ++ idx;  //如果儿子不存在，创建新结点
        p = tr[p][t];   //存入结点
    }
    cnt[p] ++ ;  //记录以这个单词结尾的数量多一个
}
void build()
{
    queue<int>que;
    for (int i = 0; i < 26; i ++ )
        if (tr[0][i])  //如果这个结点存在
            que.push(tr[0][i]);  //入队
    while (!que.empty())
    {
        int t = que.front();
        que.pop();
        for (int i = 0; i < 26; i ++ )
        {
            int p = tr[t][i];
            if (!p) //不在在转向父结点的针，直到跳向存在的结点。
                tr[t][i] = tr[ne[t]][i];
            else  //存在
            {
                ne[p] = tr[ne[t]][i];
                que.push(p);
            }
        }
    }
}
int find(char *str)
{
    int res=0;
    for (int i = 0, j = 0; str[i]; i ++ )
    {
        int t = str[i] - 'a';
        j = tr[j][t];       
        int p = j;
        while (p)
        {
            res += cnt[p];
            cnt[p] = 0;
            p = ne[p];
        }
    }
    return res;
}
int main()
{
    int T;
    scanf("%d", &T);
    while (T -- )
    {
        memset(tr, 0, sizeof tr);
        memset(cnt, 0, sizeof cnt);
        memset(ne, 0, sizeof ne);
        idx = 0;
        scanf("%d", &n);
        for (int i = 0; i < n; i ++ )
        {
            scanf("%s", str);
            insert(str);
        }
        build();
        scanf("%s", str);
        printf("%d\n", find(str));
    }
    return 0;
}

#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
const int maxn=1e6+7;
char str[maxn],key[55];
//son[maxn][26]:字典树    val[maxn]
int son[maxn][26],val[maxn];
int fail[maxn],last[maxn];
int size;
void clear()
{
    memset(son[0],0,sizeof(son[0]));size=1;
}
void clear_p(int x)
{
    memset(son[x],0,sizeof(son[x]));
    val[x]=0;
}
//加入字符串方法与 Trie 相同
void insert(char s[])
{
    int p=0;
    for(int i=0; s[i]; i++)
    {
        int u=s[i]-'a';
        if(!son[p][u])
        {
            clear_p(size);
            son[p][u]=size++;
        }
        p=son[p][u];
    }
    val[p]++;  //以这个单词结尾的数量多了一个
}
/***
处理 fail,last 指针
这里的 fail 与 KMP 中的 next 十分相似，都是在失配的时候利用之前的信息达到快速匹配的目的。
last 主要用于处理字符串包含的情况。
***/
void getfail()
{
    queue<int>q;
    fail[0]=0;
    int u=0;
    for(int i=0;i<26;i++)
    {
        u=son[0][i];
        if(u)
        {
            fail[u]=0;
            last[u]=0;
            q.push(u);
        }
    }
    while(!q.empty())
    {
        int r=q.front();
        q.pop();
        for(int i=0;i<26;i++)
        {
            u=son[r][i];
            if(!u)
            {
                son[r][i]=son[fail[r]][i];
                continue;
            }
            q.push(u);
            int v=fail[r];
            while(v&&!son[v][i]) v=fail[v];
            fail[u]=son[v][i];
            last[u]=val[fail[u]]?fail[u]:last[fail[u]];
        }
    }
}
//查找字符串的匹配情况
int find(char s[])
{
    int u=0,cnt=0;
    int len=strlen(s);
    for(int i=0;i<len;i++)
    {
        int c=s[i]-'a';
        u=son[u][c];
        int temp=0;
        if(val[u]) temp=u;
        else if(last[u]) temp=last[u];
        while(temp)
        {
            cnt+=val[temp];
            val[temp]=0;   //如果不清0，那么就会查询key 在 某个串中出现的次数
            temp=last[temp];
        }
    }
    return cnt;
}

int main()
{
    int T;
    scanf(" %d",&T);
    while(T--)
    {
        clear();
        int n;
        scanf(" %d",&n);
        getchar();
        for(int i=0;i<n;++i)
        {
            gets(key);
            insert(key);
        }
        getfail();
       gets(str);
        printf("%d\n",find(str));
    }
    return 0;
}

总结

以前只会KMP算法，今天看了许多博客，然后两本书关于AC自动的代码不是TLE就是Wrong,然后看了看输出，输出的是 key 串在最后一个串的出现次数，那么肯定会有重复的现象，显然不符合题意，现在怀疑某些书上的代码没提交过就直接印刷上去。KMP主要是一个前后缀的匹配构建next[]数组，单模式串匹配，而AC自动机是多模式串匹配，主要利用fail指针进行跳转，构建AC自动机用了一个BFS。