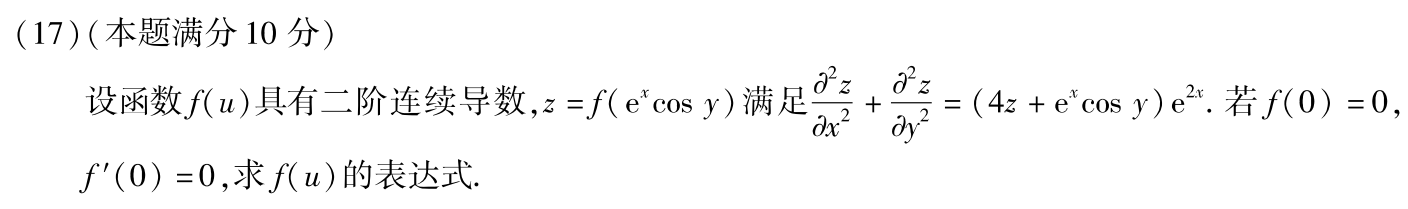1.函数的左右导数 与 导函数的左右极限
要看 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处的性质,间断?连续?可导?来判断f(x)在该点的左右导数和导函数的左右极限是否相等:
①f(x)在 x = x 0 x=x_0 x=x0处可导,则两者等价。
特例:若f(x)在 x = x 0 x=x_0 x=x0处可导,左右导数存在且为0。但导函数在 x 0 x_0 x0处震荡,则导函数的左右极限不存在。
②若f(x)在
x
=
x
0
x=x_0
x=x0处连续,且
lim
x
→
x
0
f
′
(
x
)
\lim\limits_{x→x_0}f'(x)
x→x0limf′(x)存在,则两者等价。【导数极限定理】
③若
f
(
x
)
f(x)
f(x)在该点
x
=
x
0
x=x_0
x=x0是间断的,则不可导,但导函数有左右极限。两者不等价。
④若没有给出任何条件,则两者没有关系。
1.函数的左右导数:(导数定义)
①函数的左导数:
f
′
(
x
0
−
)
=
lim
x
→
x
0
−
f
(
x
)
−
f
(
x
0
)
x
−
x
0
f'(x₀^-)=\lim\limits_{x→x₀^-}\dfrac{f(x)-f(x₀)}{x-x₀}
f′(x0−)=x→x0−limx−x0f(x)−f(x0)
②函数的右导数:
f
′
(
x
0
+
)
=
lim
x
→
x
0
+
f
(
x
)
−
f
(
x
0
)
x
−
x
0
f'(x₀^+)=\lim\limits_{x→x₀^+}\dfrac{f(x)-f(x₀)}{x-x₀}
f′(x0+)=x→x0+limx−x0f(x)−f(x0)
2.导函数的左右极限:(极限)
①导函数的左极限:
lim
x
→
x
0
−
f
′
(
x
)
\lim\limits_{x→x₀^-}f'(x)
x→x0−limf′(x)
②导函数的右极限:
lim
x
→
x
0
+
f
′
(
x
)
\lim\limits_{x→x₀^+}f'(x)
x→x0+limf′(x)
2.导数极限定理
若 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处连续 :
(1)若 lim x → x 0 f ′ ( x ) = A \lim\limits_{x→x_0}f'(x)=A x→x0limf′(x)=A 【即 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0的去心邻域内可导】,则 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处可导 且 f ′ ( x 0 ) = A f'(x_0)=A f′(x0)=A
(2)若 lim x → x 0 f ′ ( x ) = ∞ \lim\limits_{x→x_0}f'(x)=∞ x→x0limf′(x)=∞,则 f ( x ) f(x) f(x)在 x = x 0 x=x_0 x=x0处不可导
证明(1):
①姜晓千证明:
f
′
(
x
0
)
=
导数定义
lim
x
→
x
0
f
(
x
)
−
f
(
x
0
)
x
−
x
0
=
洛必达
lim
x
→
x
0
f
′
(
x
)
=
A
f'(x_0)\xlongequal[]{导数定义}\lim\limits_{x→x_0}\dfrac{f(x)-f(x_0)}{x-x_0}\xlongequal[]{洛必达}\lim\limits_{x→x_0}f'(x)=A
f′(x0)导数定义x→x0limx−x0f(x)−f(x0)洛必达x→x0limf′(x)=A
导函数的极限存在,则在去心邻域内就可导
②985数学专业 秋水 证明:
i.
lim
x
→
x
0
f
(
x
)
=
A
\lim\limits_{x→x_0}f(x)=A
x→x0limf(x)=A,则
f
(
x
)
f(x)
f(x)在
x
=
x
0
x=x_0
x=x0处连续或为第一类间断点中的可去间断点。
【不能为 跳跃间断点、第二类的无穷间断点、震荡间断点,否则极限不存在。矛盾】
ii.原函数存在定理:f(x)连续,则一定有原函数。f(x)有第一类间断点,则一定没有原函数。f(x)有第二类间断点,可能有原函数。
iii.
f
′
(
x
)
f'(x)
f′(x)有原函数
f
(
x
)
f(x)
f(x),则
f
′
(
x
)
f'(x)
f′(x)没有第一类间断点。又∵
lim
x
→
x
0
f
′
(
x
)
=
A
\lim\limits_{x→x_0}f'(x)=A
x→x0limf′(x)=A ∴
f
′
(
x
)
f'(x)
f′(x)连续
即
f
′
(
x
)
f'(x)
f′(x)不仅去心邻域内可导,
x
=
x
0
x=x₀
x=x0一点处也可导,即
f
′
(
x
0
)
=
连续
lim
x
→
x
0
f
(
x
)
=
A
f'(x_0)\xlongequal[]{连续}\lim\limits_{x→x_0}f(x)=A
f′(x0)连续x→x0limf(x)=A,即该点处可导,且导数为A
例题1:660 T154 导数极限定理
分析:
法一:直接证明
导数极限定理,前提是
f
(
x
)
f(x)
f(x)在
x
=
x
0
x=x_0
x=x0处连续。题干没有提供f(x)连续,故ABC错误。
若补充
f
(
x
)
f(x)
f(x)在
x
=
x
0
x=x_0
x=x0处连续,再加上题干原有的
lim
x
→
x
0
f
′
(
x
)
=
a
\lim\limits_{x→x_0}f'(x)=a
x→x0limf′(x)=a,则选A。
法二:排除法
举反例:分段函数
f ( x ) = { x + 1 , x ≥ 0 x , x < 0 f(x)=\left\{\begin{aligned} &x+1&,x≥0 \\ &x&,x<0 \end{aligned}\right. f(x)={x+1x,x≥0,x<0
则 lim x → x 0 f ′ ( x ) = 1 = a \lim\limits_{x→x_0}f'(x)=1=a x→x0limf′(x)=1=a,但 lim x → x 0 f ( x ) \lim\limits_{x→x_0}f(x) x→x0limf(x)不存在
答案:D
3. ∂ z ∂ x 与 ∂ f ∂ x \frac{∂z}{∂x}与 \frac{∂f}{∂x} ∂x∂z与∂x∂f
1. z = f ( u , x , y ) , u = φ ( x , y ) z=f(u,x,y),u=φ(x,y) z=f(u,x,y),u=φ(x,y) 时, ∂ z ∂ x \dfrac{∂z}{∂x} ∂x∂z与 ∂ f ∂ x \dfrac{∂f}{∂x} ∂x∂f不一样:
① ∂ z ∂ x = ∂ f ∂ u ∂ u ∂ x + ∂ f ∂ x \dfrac{∂z}{∂x}=\dfrac{∂f}{∂u}\dfrac{∂u}{∂x}+\dfrac{∂f}{∂x} ∂x∂z=∂u∂f∂x∂u+∂x∂f
② ∂ z ∂ x = ∂ f ∂ u ∂ u ∂ y + ∂ f ∂ y \dfrac{∂z}{∂x}=\dfrac{∂f}{∂u}\dfrac{∂u}{∂y}+\dfrac{∂f}{∂y} ∂x∂z=∂u∂f∂y∂u+∂y∂f
总结:
∂
z
∂
x
\dfrac{∂z}{∂x}
∂x∂z是把
y
y
y当常数,对
x
x
x里的
x
x
x 和
u
=
φ
(
x
,
y
)
u=φ(x,y)
u=φ(x,y)里的
x
x
x求偏导之和。
而
∂
f
∂
x
\dfrac{∂f}{∂x}
∂x∂f是个抽象的标记,仅是对
x
x
x里的
x
x
x求偏导。(对
u
=
φ
(
x
,
y
)
u=φ(x,y)
u=φ(x,y)里的
x
x
x求偏导则应该为:
∂
f
∂
u
∂
u
∂
x
\dfrac{∂f}{∂u}\dfrac{∂u}{∂x}
∂u∂f∂x∂u)
举例:
z
=
f
(
u
)
=
f
(
x
y
)
z=f(u)=f(xy)
z=f(u)=f(xy)
①
∂
z
∂
x
=
∂
f
∂
u
∂
u
∂
x
\dfrac{∂z}{∂x}=\dfrac{∂f}{∂u}\dfrac{∂u}{∂x}
∂x∂z=∂u∂f∂x∂u,即
z
x
′
=
f
′
⋅
y
z'_x=f'·y
zx′=f′⋅y
② ∂ z ∂ y = ∂ f ∂ u ∂ u ∂ y \dfrac{∂z}{∂y}=\dfrac{∂f}{∂u}\dfrac{∂u}{∂y} ∂y∂z=∂u∂f∂y∂u,即 z x ′ = f ′ ⋅ x z'_x=f'·x zx′=f′⋅x
例题1:14年17.
注意, z = f ( u ) = f ( e x cos y ) z=f(u)=f(e^x\cos y) z=f(u)=f(excosy)是一元函数,只有一个位置。对x求导得到的 f ′ f' f′和对y求导得到的 f ′ f' f′是一回事,没有角标。分别对x,y求二阶导得到的 f ′ ′ f'' f′′也一样。非要写角标,就都是对u, f u ′ f_u' fu′、 f u ′ ′ f_u'' fu′′
2.
因变量
=
映射关系
(
自变量
)
因变量=映射关系(自变量)
因变量=映射关系(自变量)
一元函数:
y
=
y
(
x
)
y=y(x)
y=y(x) 与
y
=
f
(
x
)
y=f(x)
y=f(x)一样
二元函数:
z
=
z
(
x
,
y
)
z=z(x,y)
z=z(x,y) 与
z
=
f
(
x
,
y
)
z=f(x,y)
z=f(x,y) 一样
因变量、映射关系、自变量,这三者更改字母是不影响的。