📝个人主页🌹：Eternity._
⏩收录专栏⏪：C++ “ 登神长阶 ”
🤡往期回顾🤡：了解 红黑树
🌹🌹期待您的关注 🌹🌹

前言： 在编程的浩瀚宇宙中，数据结构作为构建程序的基石，扮演着至关重要的角色。它们不仅定义了数据的存储方式，还极大地影响着程序的性能与效率。在众多经典数据结构中，Map（映射）和Set（集合）以其独特的性质和广泛的应用场景，成为了程序员们手中不可或缺的工具。Map允许我们根据键（Key）快速检索值（Value），而Set则提供了一种不包含重复元素的数据集合

深入理解并熟练掌握这些高级数据结构，并非一蹴而就。为了更加深刻地认识Map与Set的工作原理，以及它们背后隐藏的算法智慧，一个行之有效的方法便是亲手模拟实现它们。这一过程，不仅能够帮助我们加深对数据结构的理解，还能在实践中锻炼编程能力和问题解决能力

本文旨在为读者提供一个全面而深入的视角，通过逐步解析红黑树的基本原理、详细阐述模拟实现的过程，并辅以丰富的代码示例，帮助读者掌握红黑树Map与Set的构建与使用。我们将从最基本的二叉搜索树出发，逐步引入红黑树的特性和规则

让我们一起踏上学习的旅程，探索它带来的无尽可能！

📒1. 改造红黑树

改造红黑树以适配map和set容器，主要涉及到如何根据这两种容器的特性来设计和实现红黑树节点的存储以及相应的操作。map和set的主要区别在于它们存储的元素类型：map存储键值对（key-value pairs），而set仅存储唯一的键值（通常是键本身作为值）。尽管如此，它们在底层数据结构（如红黑树）的实现上有很多相似之处

改造内容：

• K：key的类型
• T：如果是map，则为pair<K, V>; 如果是set，则为K
• KeyOfT：通过T来获取key的一个仿函数类

// Map 与 Set
// set -> RBTree<K, K, SetKeyOfT> _t;
// map -> RBTree<K, pair<const K, V, MapKeyOfT>> _t;

红黑树的节点设计：

enum Color
{
	RED,
	BLACK
};

template<class T>
struct RBTreeNode
{
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	// pair<K, V> _kv; // 上节内容使用的这种方式
	T _data;
	Color _col;

	RBTreeNode(const T& data)
		:_left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _data(data)
		, _col(RED)
	{}
};

红黑树类的实现参考上一篇文章：红黑树类的实现
与红黑树类的不同的是Insert(插入)的类型是pair<iterator, bool>或者pair<Node*, bool>，然后还要修改内部的return返回的对象

以pair<Node*, bool>为例
代码示例：

pair<Node*, bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLACK;
			return make_pair(_root, true);
		}

		Node* parent = nullptr;
		Node* cur = _root;
		// 通过仿函数KeyOfT来比较数据的大小
		KeyOfT kot;

		while (cur)
		{
			parent = cur;
			if (kot(cur->_data) < kot(data))
			{
				cur = cur->_right;
			}
			else if (kot(cur->_data) > kot(data))
			{
				cur = cur->_left;
			}
			else
			{
				return make_pair(cur, false);
			}
		}

		// 新增节点给红色
		cur = new Node(data);
		// 注意，这里需要保存一个新增节点，以便用来返回
		Node* newnode = cur;
		cur->_col = RED;
		// 旋转变色
		return make_pair(newnode, true);;
	}

对于set，你可以简单地使用RBTree<K, K, SetKeyOfT>；而对于map，则使用RBTree<K, pair<const K, V>, MapKeyOfT>

📜2. 红黑树的迭代器

🌞迭代器基本设计

// 通过模板来达到const的迭代器的复用
template<class T, class Ref, class Ptr>
struct __TreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef __TreeIterator<T, Ref, Ptr> Self;
	Node* _node;
	
	// 构造函数
	__TreeIterator(Node* node)
		:_node(node)
	{}

	Ref operator*()
	{
		return _node->_data;
	}

	Ptr operator->()
	{
		return &(_node->_data);
	}

	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}
};

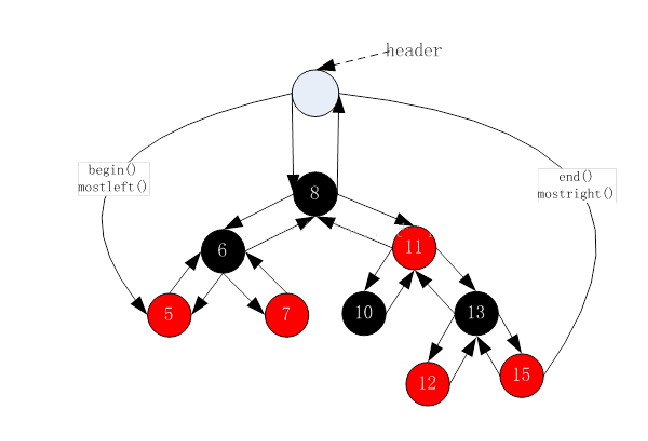
🌙begin()与end()

STL明确规定，begin()与end()代表的是一段前闭后开的区间，而对红黑树进行中序遍历后，
可以得到一个有序的序列，因此：begin()可以放在红黑树中最小节点(即最左侧节点)的位
置，end()放在最大节点(最右侧节点)的下一个位置，关键是最大节点的下一个位置在哪块？
能否给成nullptr呢？答案是行不通的，因为对end()位置的迭代器进行–操作，必须要能找最
后一个元素，此处就不行，因此最好的方式是将end()放在头结点的位置

代码示例(C++)：
(注意：此步需要在RBTree类的内部实现)，以便map,set的使用

typedef __TreeIterator<T, T&, T*> iterator;
typedef __TreeIterator<T, const T&, const T*> const_iterator;

iterator begin()
{
	Node* cur = _root;
	while (cur && cur->_left)
	{
		cur = cur->_left;
	}
	return iterator(cur);
}

iterator end()
{
	return iterator(nullptr);
}

const_iterator begin() const
{
	Node* cur = _root;
	while (cur && cur->_left)
	{
		cur = cur->_left;
	}
	return const_iterator(cur);
}

const_iterator end() const
{
 	return const_iterator(nullptr);
}

⭐operator++()与operator–()

operator++()

• 右不为空，右子树的最左节点
• 右为空，沿着到根的路径找孩子是父亲左的那个祖先

operator–()

• 左不为空，左子树的最右节点
• 左为空，沿着到根的路径找孩子是父亲右的那个祖先

注意：++和–正好是完全相反的

代码示例(C++)：

Self& operator++()
{
	if (_node->_right)
	{
		Node* cur = _node->_right;
		while (cur->_left)
		{
			cur = cur->_left;
		}
		_node = cur;
	}
	else
	{
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent && cur == parent->_right)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_node = parent;
	}
	return *this;
}

Self& operator--()
{
	if (_node->_left)
	{
		Node* cur = _node->_left;
		while (cur->_right)
		{
			cur = cur->_right;
		}
		_node = cur;
	}
	else
	{
		Node* cur = _node;
		Node* parent = cur->_parent;
		while (parent&& cur == parent->_left)
		{
			cur = parent;
			parent = cur->_parent;
		}
		_node = parent;
	}
	return *this;
}

📚3. Set的模拟实现

🧩Set的基本设计

template<class K>
class set
{
public:
	// SetKeyOfT：通过T来获取key的一个仿函数类
	struct SetKeyOfT
	{
		const K& operator()(const K& key)
		{
			return key;
		}
	};
	// typename告诉编译器这是类型，
	// 因为set不能够进行修改，所以我们用const迭代器来初始化普通迭代器，来达到不能修改的目的
	typedef typename RBTree<K, K, SetKeyOfT>::const_iterator iterator;
	typedef typename RBTree<K, K, SetKeyOfT>::const_iterator const_iterator;

	iterator begin() const
	{
		return _t.begin();
	}

	iterator end() const
	{
		return _t.end();
	}
	
	// 复用RBTree中的插入
	pair<iterator, bool> insert(const K& key)
	{
		return _t.Insert(key);
	}

private:
	RBTree<K, K, SetKeyOfT> _t;
};

📝4. Map的模拟实现

🧩Map的基本设计

template<class K, class V>
class map
{
public:
	// MapKeyOfT：通过pair来获取kv.first的一个仿函数类
	struct MapKeyOfT
	{
		const K& operator()(const pair<K, V>& kv)
		{
			return kv.first;
		}
	};
	
	// map是一个key不能修改，value能够修改的结构
	typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator iterator;
	typedef typename RBTree<K, pair<const K, V>, MapKeyOfT>::iterator const_iterator;

	iterator begin()
	{
		return _t.begin();
	}

	iterator end()
	{
		return _t.end();
	}
	
	// 重载map中的operatorp[]
	// operatorp[] 当原数据中没有时，插入并初始化，有则修改second
	V& operator[](const K& key)
	{
		// 没有是插入，有则是查找
		pair<iterator, bool> ret = insert(make_pair(key, V()));
		return ret.first->second;
	}
	
	// 复用RBTree中的插入
	pair<iterator, bool> insert(const pair<K, V>& kv)
	{
		return _t.Insert(kv);
	}
	
private:
	RBTree<K, pair<const K, V>, MapKeyOfT> _t;
};

📖5. 总结

随着我们对红黑树Map与Set的深入探索与模拟实现，这场高效数据存储的旅程也即将画上圆满的句号。回望这段旅程，我们从红黑树的基本概念出发，逐步揭示了其保持平衡、实现高效操作的秘密，并通过亲手编写代码，将理论转化为了实践

同时，我们也要意识到，数据结构的选择并非一成不变。在实际应用中，我们需要根据具体需求、数据规模、性能要求等因素综合考虑，选择最合适的数据结构来解决问题。只有这样，我们才能真正做到高效、稳定地处理数据。

然而，学习之路永无止境。红黑树只是众多高效数据结构中的一种，它们各自有着独特的优势和适用场景。在未来的学习与实践中，我们还需要继续探索其他数据结构，如AVL树、B树、B+树等，以拓宽我们的视野，提升我们的技能

希望各位在未来的学习与工作中，保持对知识的渴望与追求，勇于挑战自我，不断探索未知领域。相信在不久的将来，你们定能在数据处理的广阔舞台上大放异彩！

希望本文能够为你提供有益的参考和启示，让我们一起在编程的道路上不断前行！
谢谢大家支持本篇到这里就结束了，祝大家天天开心！