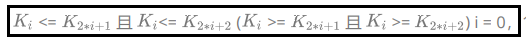💯💯💯
本文详细的介绍堆是什么,堆的结构以及堆是如何实现的,本篇重点在于堆的两个调整算法,掌握它们,你就基本可以理解堆是如何实现的,以及堆的应用:堆排序。本篇带有图文解析及代码以供参考。
⏰1.堆的概念
如果有一个集合K,有n个元素,把它们按照完全二叉树的顺序存储方式存储在一个一维数组中,并满足
则称为小堆或者大堆。将根节点最大的堆叫做最大堆或大根堆,根结点最小的堆叫做最小堆或小根堆。
理解起来也很简单。
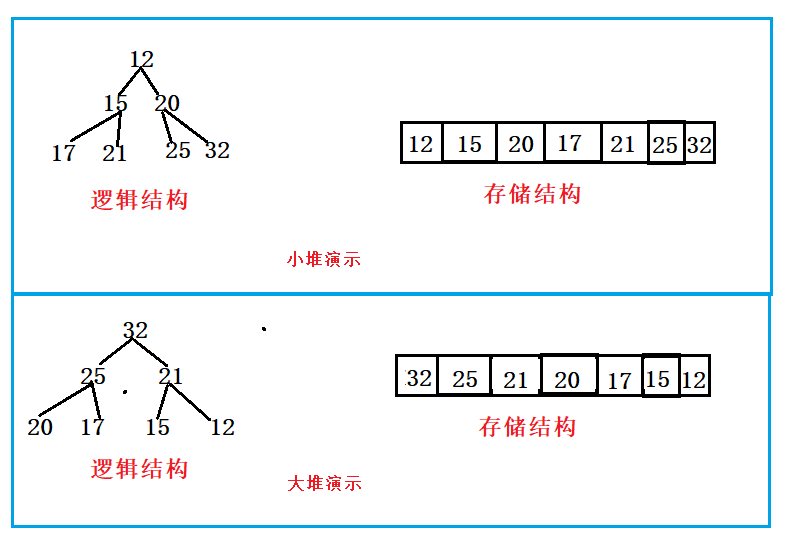
小堆就是每个父节点都小于子结点
大堆就是每个父节点都大于子结点
堆的性质:
- 堆中某个结点的值总是不小于或不大于其父结点的值
- 堆总是一颗完全二叉树。
⏰2.堆的结构
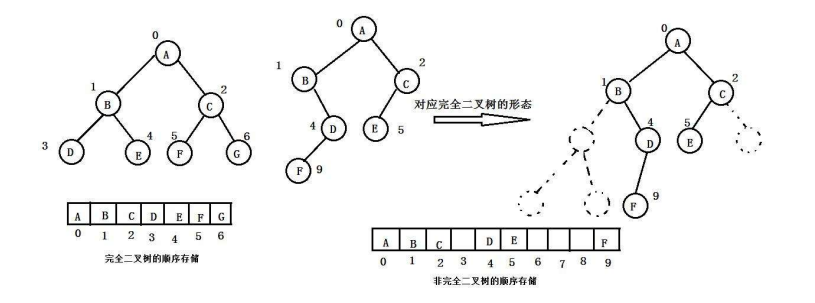
堆的存储结构是顺序结构,也就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为如果不是完全二叉树就会有空间的浪费。而现时使用中只有堆才会使用数组来存储。
二叉树顺序存储在物理上是一个数组,在逻辑上是一个二叉树
⏰3.堆的算法
要实现堆,我们需要理解两个重要的算法:向上调整和向下调整算法。
🕑3.1堆向上调整算法
堆的向上调整算法,我们常用在堆的插入中,当我们要将一个数据插入到堆中,该怎么插入呢?
该算法的思想就是:
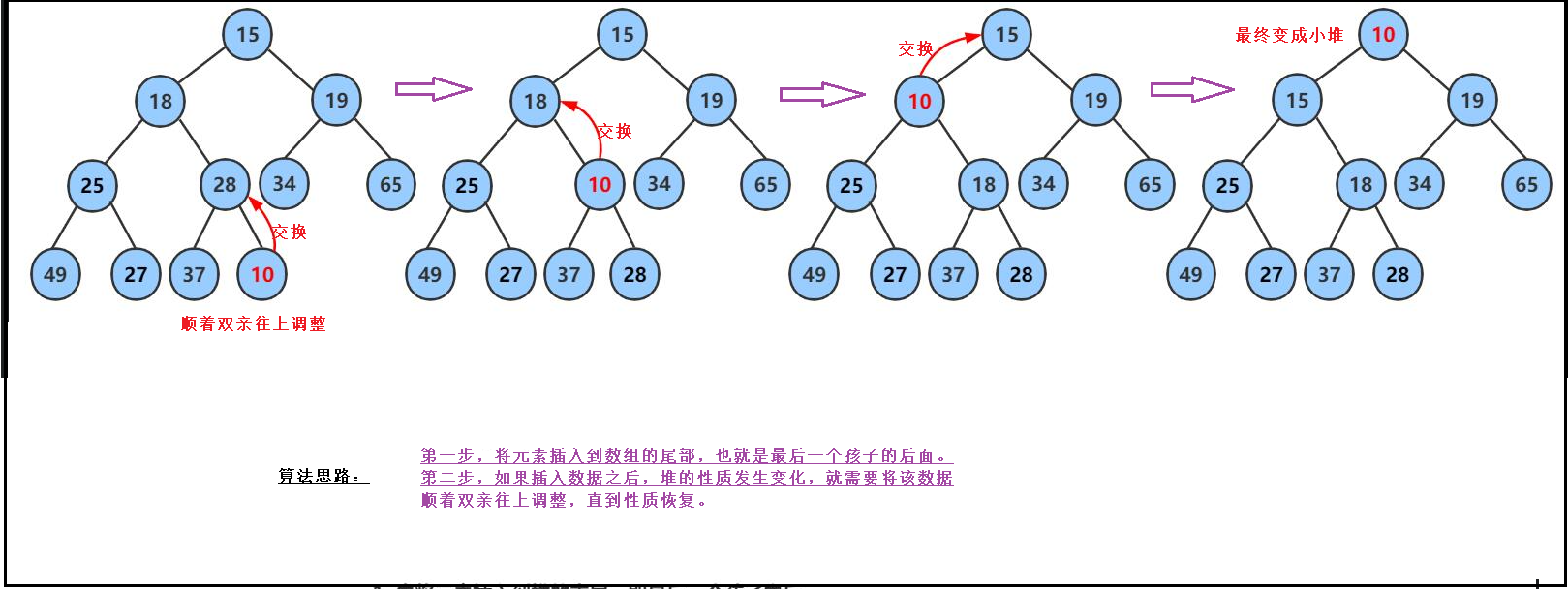
第一步,将元素插入到数组的尾部,也就是最后一个孩子的后面。
第二步,如果插入数据之后,堆的性质发生变化,就需要将该数据顺着双亲往上调整,直到性质恢复。
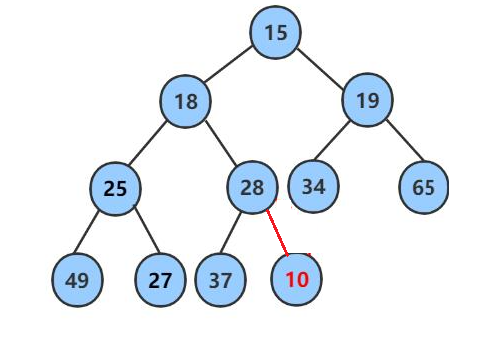
比如现在有一个小堆
我想插入一个数据10进去,第一步,就是将数据插入到堆的尾部去,也就是最后一个孩子的后面去。
第二步,将数据插入堆后,发现堆的性质发生改变,原来是一个小堆,每个父节点都小于子结点的,但由于插入的数据,导致这一性质改变,所以我们需要将该新结点往上调整,顺着它的双亲走就可以,因为只有它这个地方发生了改变。
怎么调整呢?
只要让插入的新结点与它的父节点进行比较,如果大于父节点,不做改变,如果小于父节点,则两个结点值交换。
交换完后,还需要让这个父节点与它的父节点进行比较,小于它的父节点就要往上调整,直到父节点小于0为止。
这个过程其实就是不断的迭代,孩子child到父亲位置上去,父亲再到新的父亲上去。
而向上调整法使用有一个前提:向上调整的前提就是child之前的数是堆,不然无法使用向上调整法调整。
void Swap(HPDataType* a, HPDataType* b)//交换函数
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustUp(HPDataType* a, int child)//向上调整的前提就是child之前的数是堆
{
int parent = (child - 1) / 2;//首先记录新插入结点的父节点位置
while (child > 0)
{
if (a[child] > a[parent])//【大堆】如果子结点比父节点大
{
Swap(&a[child],&a[parent]);//那就将两个结点值交换
child = parent;//交换完后接着比,孩子跑到父亲的位置上去
parent = (child - 1) / 2;//父亲更新到新的父亲上去
}
else
{
break;//走到这里表明子节点比父节点小,满足堆的性质,结束比较
}
}
}
🕒3.2堆向下调整算法
堆的向下调整算法通常用在堆的删除,堆的调整上。
向下调整肯定要调整的数据在顶上。也就是堆顶。
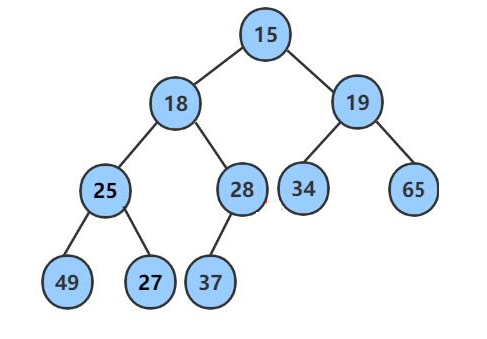
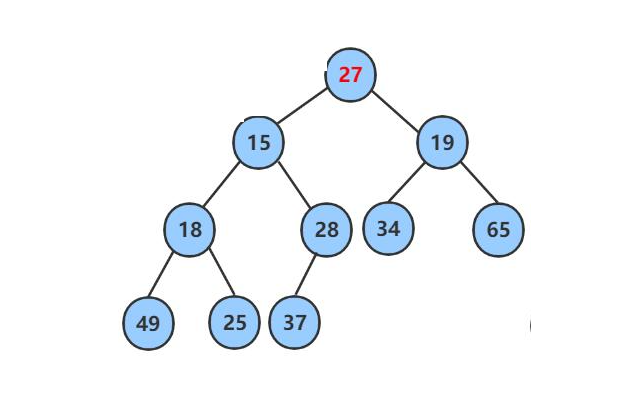
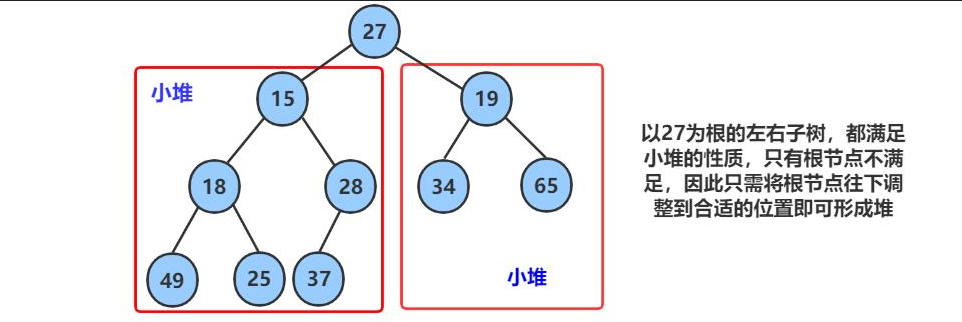
比如给定一个完全二叉树,从逻辑上看是二叉树,其实是一个数组 观察发现,只有最上面的27不满足小堆的条件,其他都满足父节点小于子节点性质,那如何将它调整成小堆呢?
因为27在堆顶,肯定要往下调,那怎么调呢?
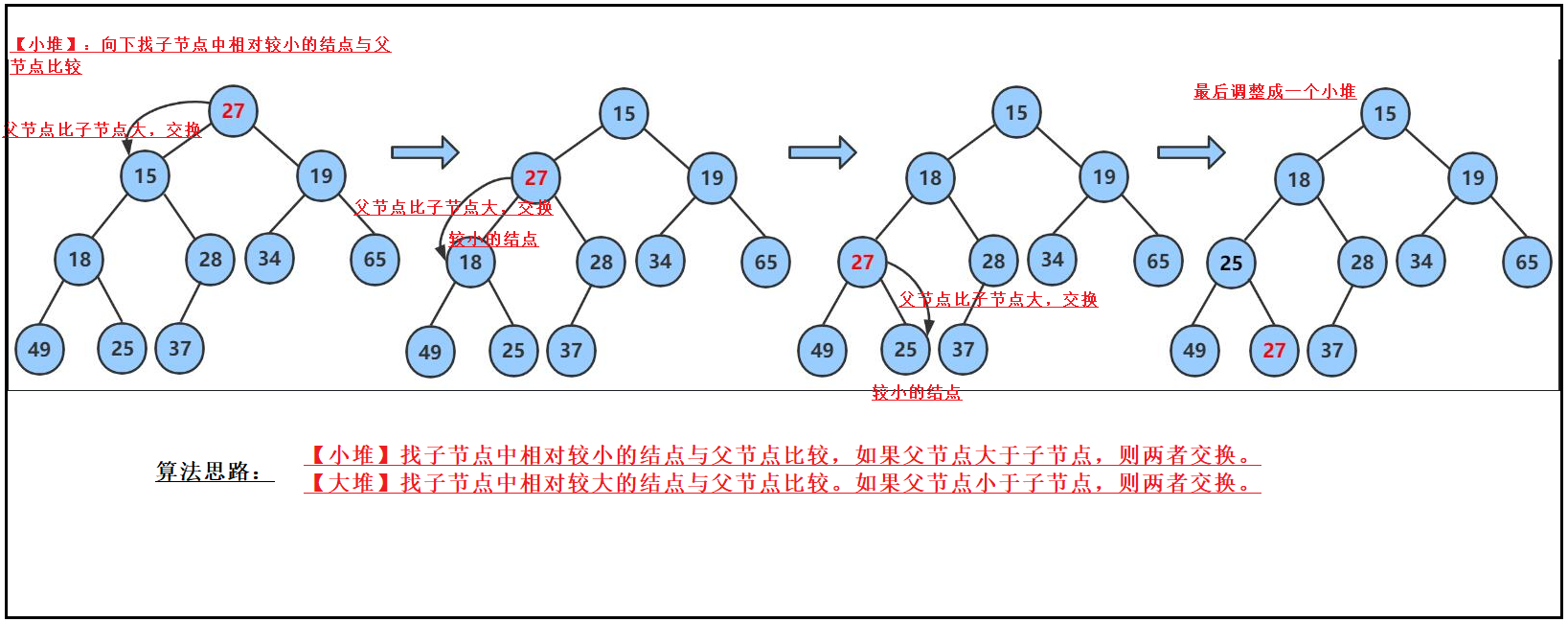
该算法的思路就是:
【小堆】找子节点中相对较小的结点与父节点比较,如果父节点大于子节点,则两者交换。
【大堆】找子节点中相对较大的结点与父节点比较。如果父节点小于子节点,则两者交换。
void AdjustDown(HPDataType* a, int n, int parent)//实现的前提是左右子树都是堆
{
int child = parent * 2+1;//先记录下子节点的位置
while (child < n)
{
//【大堆】选出左右孩子中比较大的孩子,假设child为左边,假设左边孩子比较大
if (child+1<n&&a[child] < a[child + 1])//不过这里存在越界的风险,不能保证右边的孩子一定存在
{//右边的孩子要存在的话也需要小于n才可以所以我们再加上去
++child;//让右边的孩子成为比较大的child
}
//然后让根(父亲)与较大儿子比较,这里是大堆,父亲要大于儿子的
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
//交互完后,让parent跳到儿子位置上去,儿子继续往下找
parent = child;
child = parent* 2+1;
}
else
{
break;//走到这里表示符合大堆性质
}
}
}
不过要注意的是,向下调整算法使用也是有前提的:左右子树必须是一个堆才可以进行调整。
⏰4.堆的实现
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}Hp;
//堆的初始化
void HpInit(Hp* ps);
//堆的插入
void HpPush(Hp* ps, HPDataType x);
//堆向上调整
void AdjustUp(HpDataType*a,int child);
//交换数据
void Swap(HpDataType* a, HpDataType* b);
//堆向下调整
void AdjustDown(HpDataType* a, int n, int parent);
//堆的删除
void HpPop(Hp* ps);
//获取堆顶数据
HPDataType HpTop(Hp* ps);
//判断堆是否为空
bool HpEmpty(Hp* ps);
//获取堆的有效数据的大小
int HpSize(Hp* ps);
🕓4.1堆的初始化
堆是由数组构成,跟顺序表一样,有容量,大小,数组空间是动态开辟的。
那初始化都需要将变量置0,将数组空间先开辟好。
void HpInit(Hp* ps)//初始化
{
assert(ps);//断言判断是否为空
ps->a =(HPDataType*)malloc(sizeof(HPDataType)*4);//一上来给数组开辟4个整形大小
if (ps->a == NULL)
{
perror("malloc");
}
ps->capacity = 4;//容量先确定下
ps->size = 0;//大小为0
}
🕕4.2堆的插入
堆的插入就需要用到向上调整法了,将插入到堆尾巴的数据顺着双亲往上比较,【大堆】子节点大于父节点的,两个值就需要交换。
还有细节问题:当堆满了时,需要动态扩容。
void Swap(HPDataType* a, HPDataType* b)//将交换操作写成函数,因为向下调整也需要用到,所以最好分装成一个函数。
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustUp(HPDataType* a, int child)//向上调整的前提就是child之前的数是堆
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child],&a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HpPush(Hp* ps, HPDataType x)//向堆里插入数据
{
assert(ps);
//插入数据之前需要判断一下,堆是否满了,是否需要扩容
if (ps->size == ps->capacity)
{
HPDataType* tmp = realloc(ps->a, sizeof(HPDataType) * ps->capacity * 2);//每次扩容两倍
if (tmp == NULL)
{
perror("realloc");
}
ps->a = tmp;//如果扩容成功,则将扩容的空间赋给数组a
ps->capacity *= 2;
}
ps->a[ps->size] = x;
//因为下标从0开始,先插入数据后,size再进行++
ps->size++;//这时的size才是++后的size
//插入一个数据很简单,但是要考虑是否满足堆的性质;
//向上调整
AdjustUp(ps->a, ps->size - 1);//size-1就是要插入的位置 堆尾部
}
🕖4.3堆的删除
堆的删除,需要用到向下调整,想一想,堆删除是删除堆顶的还是删除堆最后一个呢?
【大堆】堆顶是最大值,当删除堆顶时,我们就可以获取最大值,当最大值删除后,我们才有可能获取次大的,次大的删除,才可以获取次次大的,所以删除堆顶数据是有意义的,这样就可以快速获取前面的数值了。TOP-k问题也是类似的。
而如果删除堆尾部的数据,根本没有什么意义所在。
那该如何删除堆顶数据呢?
【误区】我们如果直接删除堆顶数据的话,那么剩下的数据就会混乱,原来的关系就会破裂,就无法再构成一个堆,所以不能直接删除堆顶数据。
【方法】所以我们采取这样的做法:
1.将堆顶数据与堆尾部最后一个数据交换。
2.然后删除最后一个数据。
3.让换到堆顶的数据使用向下调整算法进行调整,使其恢复原来的性质。
【优点】这样做的好处就是,基本不会改变左右子树的结构。
void Swap(HPDataType* a, HPDataType* b)//将交换操作写成函数,因为向下调整也需要用到,所以最好分装成一个函数。
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustDown(HPDataType* a, int n, int parent)//实现的前提是左右子树都是堆
{
int child = parent * 2+1;
while (child < n)
{
//选出左右孩子中比较大的孩子,假设child为左边,假设左边孩子比较大
if (child+1<n&&a[child] < a[child + 1])//不过这里存在越界的风险,不能保证右边的孩子一定存在
{//右边的孩子要存在的话也需要小于n才可以所以我们再加上去
++child;//让右边的孩子成为比较大的child
}
//然后让根(父亲)与较大儿子比较,这里是大堆,父亲要大于儿子的
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
//交互完后,让parent跳到儿子位置上去,儿子继续往下找
parent = child;
child = parent* 2+1;
}
else
{
break;
}
}
}
void HpPop(Hp* ps)
{
assert(ps);
//当堆被删空时,需要判断下
assert(!HpEmpty(ps));
//交换堆头数据和子叶数据
Swap(&ps->a[0], &ps->a[ps->size - 1]);
ps->size--;//删除堆尾部数据
//交换完后,需要使用向下调整:来调整堆
AdjustDown(ps->a, ps->size, 0);
}
🕗4.4获取堆顶数据
HPDataType HpTop(Hp* ps)//获取堆顶数据
{
assert(ps);
return ps->a[0];//堆顶的数据就是数值首元素
}
🕓4.5堆的数据个数
int HpSize(Hp* ps)//获取堆的有效数据的大小
{
assert(ps);
return ps->size;
}
🕐4.6堆的判空
bool HpEmpty(Hp* ps)//判断堆是否为空
{
assert(ps);
return ps->size == 0;//当size为0时表示堆为空
}
🕚4.7堆的销毁
但凡堆开辟的都要销毁
void HpDestroy(Hp* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = 0;
ps->size = 0;
free(ps);
ps = NULL;
}
🕦4.8堆的创建【调堆】
在已有数据的基础上我们进行调堆
下面我们给出一个数组,这个数组逻辑上可以看做一颗完全二叉树,但是还不是一个堆,现在我们通过算
法,把它构建成一个堆。根节点左右子树不是堆,我们怎么调整呢?这里我们从倒数的第一个非叶子节点的
子树开始调整,一直调整到根节点的树,就可以调整成堆。
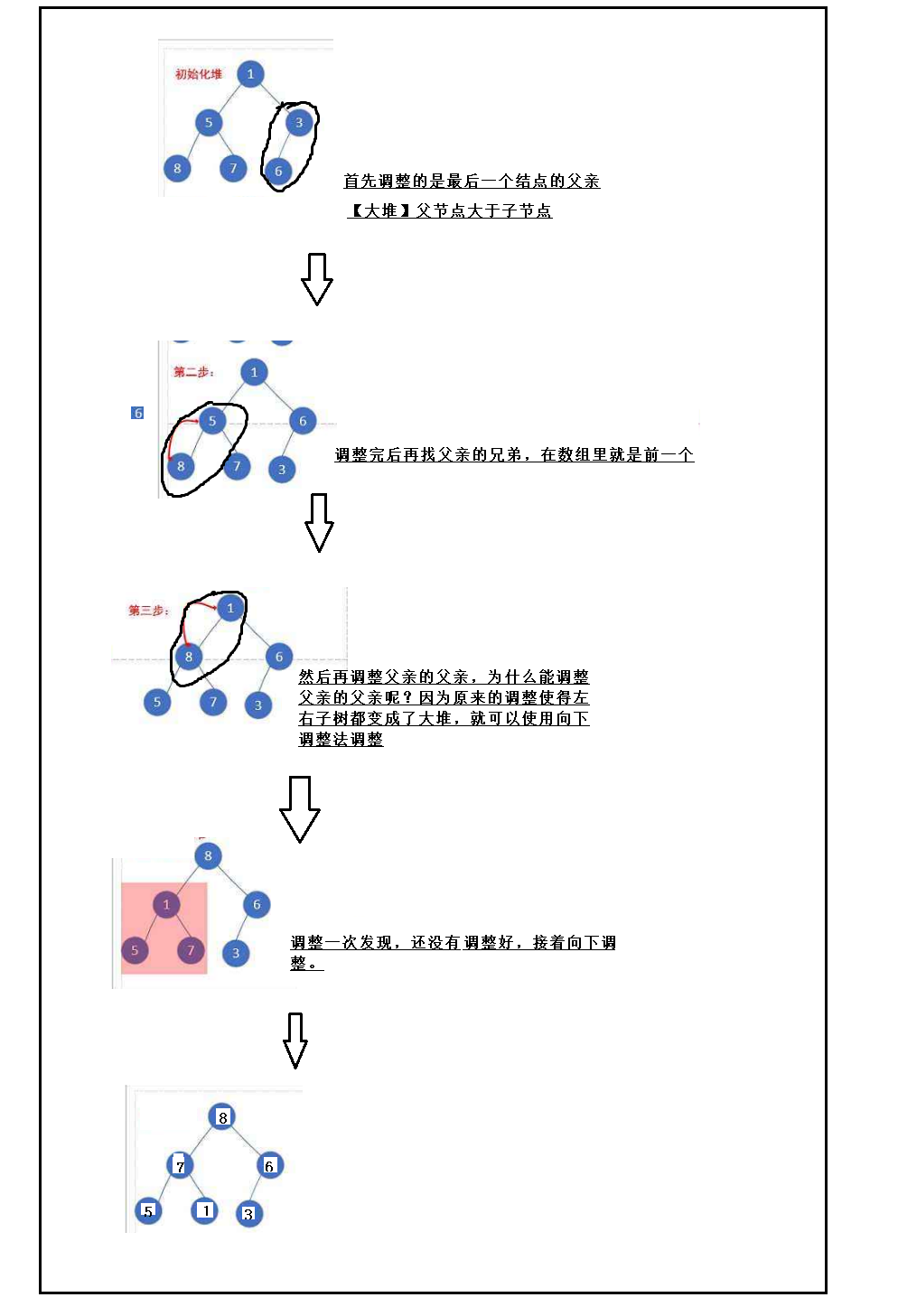
int a[] = {1,5,3,8,7,6};
倒数第一个非叶子,或者最后一个叶子的父亲。
为什么这样调?
我们知道,向下调整有前提条件,要求左右子树都为大堆或小堆。
我们从后面开始调,从最后一个叶子的父亲开始调,调完父亲,再调父亲的兄弟,那父亲和兄弟都调整完,父亲的父亲就可以调整了,因为父亲和兄弟那串子树都为堆了已经。 只要左右子树为堆我们就可以用向下调整。
不过我们也可以利用向上调整法进行模拟插入建堆。
⏰5.实现堆的代码
Heap.h
#pragma once
#include <assert.h>
#include <stdlib.h>
#include <stdio.h>
#include <stdbool.h>
typedef int HPDataType;
typedef struct Heap
{
HPDataType* a;
int size;
int capacity;
}Hp;
void HpInit(Hp* ps);//初始化
void HpPush(Hp* ps, HPDataType x);//插入数据
void AdjustUp(HPDataType* a, int child);//向上调整
void Swap(HPDataType* a, HPDataType* b);//交换数据
void AdjustDown(HPDataType* a, int n, int parent);//向下调整
void HpPop(Hp* ps);
//堆删除数据,规则是删除堆顶的数据:意义是什么?删除最大的老二才能找到,老二删除,老三才能找到,有助于快速找到前几名
//【优点】向下调整--第一个和最后一个交换,不会影响堆的大结构兄弟还是兄弟,父子还是父子
//【交换堆顶数据和最后一个数据】
//【删除数据】--即可
//【向下调整】--哪个儿子大就和哪个儿子比
//【结束标志】子叶就是结束标志,因为子叶没有儿子,因为儿子下标超出数组大小了
HPDataType HpTop(Hp* ps);//获取堆顶数据
bool HpEmpty(Hp* ps);//判断堆是否为空
int HpSize(Hp* ps);//获取堆的有效数据的大小
Heap.c
#include "heap.h"
void HpInit(Hp* ps)//初始化
{
assert(ps);
ps->a =(HPDataType*)malloc(sizeof(HPDataType)*4);
if (ps->a == NULL)
{
perror("malloc");
}
ps->capacity = 4;
ps->size = 0;
}
void Swap(HPDataType* a, HPDataType* b)
{
HPDataType tmp = *a;
*a = *b;
*b = tmp;
}
void AdjustUp(HPDataType* a, int child)//向上调整的前提就是child之前的数是堆
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (a[child] > a[parent])
{
Swap(&a[child],&a[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
void HpPush(Hp* ps, HPDataType x)//向堆里插入数据
{
assert(ps);
//插入数据之前需要判断一下,堆是否满了,是否需要扩容
if (ps->size == ps->capacity)
{
HPDataType* tmp = realloc(ps->a, sizeof(HPDataType) * ps->capacity * 2);
if (tmp == NULL)
{
perror("realloc");
}
ps->a = tmp;
ps->capacity *= 2;
}
ps->a[ps->size] = x;
//因为下标从0开始,先插入数据后,size再进行++
ps->size++;//这时的size才是++后的size
//插入一个数据很简单,但是要考虑是否满足规则;size-1就是要插入的位置
//向上调整
AdjustUp(ps->a, ps->size - 1);
}
void AdjustDown(HPDataType* a, int n, int parent)//实现的前提是左右子树都是堆
{
int child = parent * 2+1;
while (child < n)
{
//选出左右孩子中比较大的孩子,假设child为左边,假设左边孩子比较大
if (child+1<n&&a[child] < a[child + 1])//不过这里存在越界的风险,不能保证右边的孩子一定存在
{//右边的孩子要存在的话也需要小于n才可以所以我们再加上去
++child;//让右边的孩子成为比较大的child
}
//然后让根(父亲)与较大儿子比较,这里是大堆,父亲要大于儿子的
if (a[parent] < a[child])
{
Swap(&a[parent], &a[child]);
//交互完后,让parent跳到儿子位置上去,儿子继续往下找
parent = child;
child = parent* 2+1;
}
else
{
break;
}
}
}
void HpPop(Hp* ps)
{
assert(ps);
//当堆被删空时,需要判断下
assert(!HpEmpty(ps));
//交换堆头数据和子叶数据
Swap(&ps->a[0], &ps->a[ps->size - 1]);
ps->size--;
//交换完后,需要使用向下调整:来调整堆
AdjustDown(ps->a, ps->size, 0);
}
HPDataType HpTop(Hp* ps)//获取堆顶数据
{
assert(ps);
return ps->a[0];
}
bool HpEmpty(Hp* ps)//判断堆是否为空
{
assert(ps);
return ps->size == 0;
}
int HpSize(Hp* ps)//获取堆的有效数据的大小
{
assert(ps);
return ps->size;
}
void HpDestroy(Hp* ps)
{
assert(ps);
free(ps->a);
ps->a = NULL;
ps->capacity = 0;
ps->size = 0;
free(ps);
ps = NULL;
}