我在很久之前就已经接触了约瑟夫问题了，但是最近终于找到了时间效率比较优秀的解决办法，写一篇博客以纪念一下。

什么是“约瑟夫问题”？

以下内容来自百度百科：（可以忽略以下三段内容）

约瑟夫问题（有时也称为约瑟夫斯置换，是一个出现在计算机科学和数学中的问题。在计算机编程的算法中，类似问题又称为约瑟夫环。又称“丢手绢问题”.）

关于它的故事：

据说著名犹太历史学家 Josephus有过以下的故事：在罗马人占领乔塔帕特后，39
个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。然而Josephus
和他的朋友并不想遵从。首先从一个人开始，越过k-2个人（因为第一个人已经被越过），并杀掉第k个人。接着，再越过k-1个人，并杀掉第k个人。这个过程沿着圆圈一直进行，直到最终只剩下一个人留下，这个人就可以继续活着。问题是，给定了和，一开始要站在什么地方才能避免被处决？Josephus要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

另一个故事：

17世纪的法国数学家加斯帕在《数目的游戏问题》中讲了这样一个故事：15个教徒和15
个非教徒在深海上遇险，必须将一半的人投入海中，其余的人才能幸免于难，于是想了一个办法：30个人围成一圆圈，从第一个人开始依次报数，每数到第九个人就将他扔入大海，如此循环进行直到仅余15个人为止。问怎样排法，才能使每次投入大海的都是非教徒。

下文中所介绍的问题与上面的两个类似，我们称它为“约瑟夫序列模型”。它的内容如下：

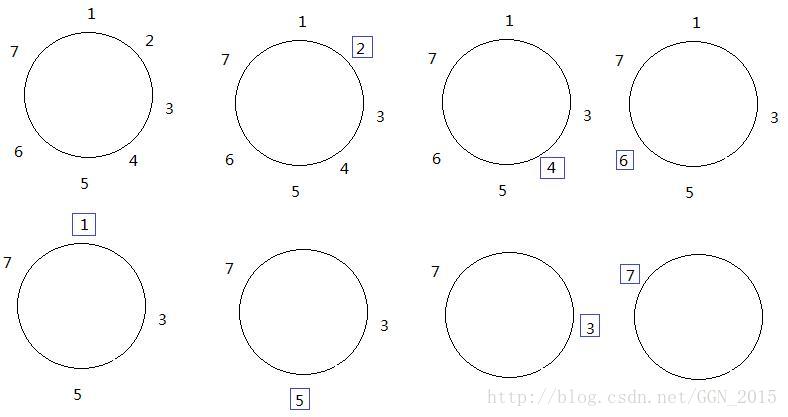
若干个人排成一圈，按照顺时针编号为1~n。从一号开始对环进行如下处理：1号人跳过，2号出环，3号跳过，4号出环，5号跳过（即每隔一个人，出圈一个人）…又因为所有的人站成一个环，最终所有的人一定都会出环（最后剩下的那个人被看成是最后一个出环的人）。用这种方法，我们把每个人按照出圈次序排序，就得到了一个“出圈序列”，下文中称其为“约瑟夫序列”。

如上图，$n=7$时的约瑟夫序列为：$\{A_n\}=\{2,4,6,1,5,3,7\}$。

问题1：快速计算约瑟夫序列末尾元素

——每个人都想成为笑到最后的人，所以他总是想找到最后一个出圈的位置。

本题的一种暴力做法是用链表去模拟，但其时间效率比较差（如果只是求末尾元素的话。）

首先，无论n是奇数还是偶数，一个编号为偶数的位置一定不可能成为最后一个出圈的位置，因为在第一趟走的时候这些位置就会出圈，剩下的是所有的奇数。

此时我们不妨将所有的奇数重新编号为$1..\lceil \frac{n}{2} \rceil$。你可以找到重新编号后的最后一个出圈的编号，然后再把它还原回它原来的编号。

我们不妨令$J(n)$表示长度为n的约瑟夫序列的末尾元素。

首先分析当n为偶数时的情况（令$n=2n$）：

第一步：所有的偶数位置被弹出。

第二步：将奇数序列$\{1,3,5,..,2n-1\}$通过函数$f(x)=\frac{x+1}{2}$映射到新的编号$\{1,2,3,...,n\}$。然后递归的求解$J(n)$，再通过$f(x)$的反函数$f^{-1}(x)=2x-1$得到原序列中这个位置中的编号：

即：$J(2n)=2J(n)-1|n \in N^*$

然后再分析当n为奇数时的情况（令$n=2n+1$）：

第一步：将所有偶数位置弹出。

第二步：因为序列的总长度为奇数，所以下一个出圈的一定是编号为1的那个人。

第三步：把现在剩下的人的序列$\{3,5,7,..,2n+1\}$按照函数$f(x)=\frac{x-1}{2}$重新编号为$\{1,2,3,..,n\}$，然后递归求解$J(n)$，再通过$f(x)$的反函数$f^{-1}(x)=2x+1$得到原序列中这个位置的编号：

即：$J(2n+1)=2J(n)+1|n \in N^*$

边界条件：$J(1)=1$（只有一个人的话，他当然就是被剩下的人。）

程序写出来近乎脑残：

int J(int n){
    if(n==1)return 1;
    if(n%2==0)
        return 2*J(n/2)-1;
    return 2*J(n/2)+1;
}

它的时间复杂度为$O(lg(n))$，因为n每次至少缩减为原范围的一半。

关于问题1的进一步探索

打一个表，看看函数$J(n)$还有什么神奇的性质：

#include<cstdio>

int J(int n){
    if(n==1)return 1;
    if(n%2==0)
        return 2*J(n/2)-1;
    return 2*J(n/2)+1;
}

int main(){
    printf("  i :");
    for(int i=1;i<=15;i++)
        printf("%5d",i);
    printf("\n");
    printf("J(i):");
    for(int i=1;i<=15;i++)
        printf("%5d",J(i));
    printf("\n");
    return 0;
}

可以打出来这样的一个表：

  i :    1    2    3    4    5    6    7    8    9   10   11   12   13   14   15
J(i):    1    1    3    1    3    5    7    1    3    5    7    9   11   13   15 

不难发现一些神奇的规律：

序列J可以看成是若干个奇数等差数列的拼接$\{\{1\},\{1,3\},\{1,3,5,7\},\{1,3,5,7,9,11,13,15\}...\}$而这些奇数等差数列的长度恰好为2的若干次幂：$\{1,2,4,8...\}$。

这个性质可用$J(2^m+l)=2l+1：m \in N, 0 \leq l < 2^m$表示。

这个性质可以用数学归纳法证明：

定义命题$P(x) \Leftrightarrow J(2^x+l)=2l+1：m \in N, 0 \leq l < 2^m$

1.$x=0$该命题显然成立。

2.当该性质已经关于$1..x-1$成立，那么：

(1)令$l$为偶数：

(2)令$l$为奇数：

p.s. 因为$0 \leq l < 2^m$所以有$0 \leq \frac{l}{2} < 2^{m-1}$（$l$为偶数）和$0 \leq \frac{l-1}{2} < 2^{m-1}$（$l$为奇数）

因此得证。

问题2：快速计算某一个人的出圈时间

不妨令$f(n,k)$表示一个长度为n的约瑟夫序列中，元素k在其中的位置。

当$k$是偶数的时候，（想都不用想）$f(n,k)=\frac{k}{2}$。

当$k$是奇数的时候呢？

1.n是偶数，令$n=2n$。

同之前求最后一个出队人的方法一样，先去掉所有编号为偶数的人，然后给剩下的人重新编号为$1..n$。编号函数为$g(x)=\frac {x+1}{2}$。求出这个人转换后的编号在n个人中的出圈时刻再+n即为答案。

即：$f(2n,k)=n+f(n,\frac {k+1}{2})$

2.n是奇数，令$n=2n+1$。

方法同上，先去掉所有的偶数以及1，将$\{3,5,7,..,2n+1\}$重新编号为$\{1,2,3,..,n\}$。编号函数为$g(x)=\frac {x-1}{2}$。计算结果+(n+1)即为答案。

即：$f(2n+1,k)=n+1+f(n,\frac {x-1}{2})$以及$f(2n+1,1)=n+1$

这样看可能有点复杂，我们不妨令$f(n,0)=0$，这样的话，$f(2n+1,1)=n+1$的情况就会被并入$f(2n+1,k)=n+1+f(n,\frac {x-1}{2})$中。

程序还是那么的水：

int f(int n,int k){
    if(k%2==0)return k/2;//k=0 included
    if(n%2==0)return n/2+f(n/2,(k+1)/2);
    return (n+1)/2+f((n-1)/2,(k-1)/2);
}

很显然的是时间复杂度仍然是$O(lg(n))$。

如有谬误，敬请指正！