2018.6.23 好久没写博客了，做了一道有趣的分治题，写个博客。

题目传送门： P1429 平面最近点对（加强版）

题意

题目描述

给定平面上n个点，找出其中的一对点的距离，使得在这n个点的所有点对中，该距离为所有点对中最小的

输入格式

第一行：n；2≤n≤200000

接下来n行：每行两个实数：x y (0≤x,y≤10^9)，表示一个点的行坐标和列坐标，中间用一个空格隔开。

输出格式

仅一行，一个实数，表示最短距离，精确到小数点后面4位。

解题思路

众所周知，这道题可以分治解决。我们可以对这n个点，以x坐标为第一关键字，y坐标为第二关键字排序。排序后，我们可以把这个点集等分成左右两部分。这样分割以后，所有有可能成为答案的点对就被分为了三部分——1.两个点都在左侧集合，2.两个点都在右侧集合，3.一个点在左侧集合、另一个点在右侧集合。

对于两个点在同一个集合的点对，我们可以递归求解。但对于两个点不在同一个集合的最近点对的求解，却是很棘手的。如果暴力在两侧枚举点然后求距离，时间复杂度就会退化为$O(n^2)$，分治就没有意义了。

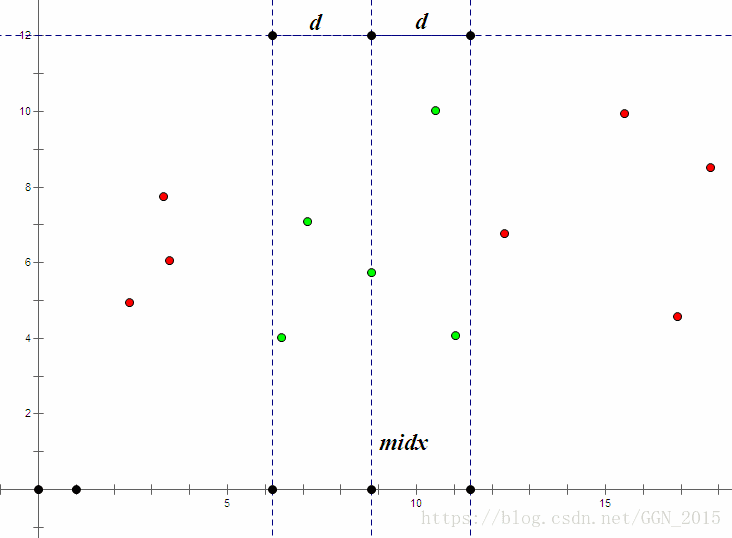
其实在两侧暴力枚举点，会得到很多多余的信息。如果在分治处理左右两边的时候，已经求出的最近点对距离为d（d为左半集合答案 与 右半集合答案 的较小值），那么如果我们能确定左侧的一个点到右侧的任何一个点的距离一定大于d的话，那么这个点在枚举点的过程中是可以直接被忽略的。这样，我们可以把左侧集合最靠右的点的横坐标 记为$midx$，如果一个点的横坐标x满足$|x-midx|\ge d$，就不需要再考虑这个点了，需要考虑的点只有中间一个“竖条”中的点。

上图中绿色的点是可能对答案造成贡献的点，横坐标小于等于midx的点集为左侧集合，剩余的点是右侧集合。（黑点是辅助作图用的，请忽视这些点）

如果在中间这个竖条中暴力枚举点对的话时间复杂度还是不对的（总时间复杂度仍是$O(n^2)$），我们还可以进行进一步的优化——如果两个点的纵坐标的差的绝对值大于d，那么它们间的距离也一定不小于d。这样我们可以把所有绿点取出来，再按照y坐标为第一关键字，x坐标为第二关键字排序（其实有没有第二关键字无所谓），按照y坐标从小到大依次考虑每个点i与它后面（即纵坐标大于等于它的点）的所有点j之间的距离，如果i与j的纵坐标差大于等于d就退出循环，不再继续枚举j了，这样一定也可以得到正确的结果。

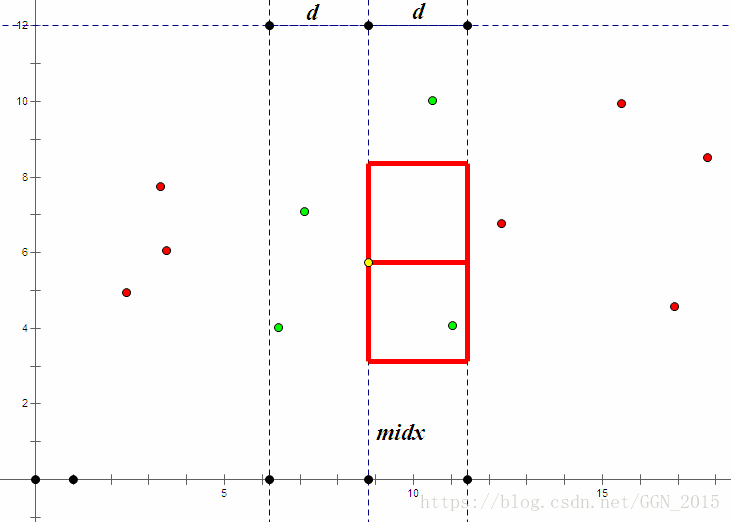
其实这个算法的时间复杂度已经是$O(n{\log }^{2}n)$的了，这是为什么呢？因为我们在枚举j时，会及时break，所以对于某一个点，有机会与它求距离点一定都在一个面积为$2d^2$的“日”字形区域中。

上图的”日“字形为两个边长为d的正方形组成，是有机会与黄点求距离的点坐标的可能范围。这个范围很小，以至于这个范围内的点一定不会超过6个！这真是个惊人的结论，我们现在来证明这一点。

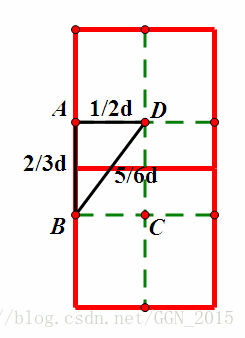
因为这个日字形隶属于右半部分，右半部分的任意两个点间的距离又一定是大于等于d的（根据前文d的定义可知），所以“日”字形中包含的所有点对的距离也应该是大于等于d的。我们可以把这个“日”字进行一个巧妙的划分。

对于长度为2d边，我们取其三等分点；对于长度为d的边，我们取其中点。这样，我们就把这个日字形划分为六个面积相等的小矩形。矩形的长为$\frac{2}{3}d$，宽为$\frac{1}{2}d$，根据勾股定理可知，改矩形的对角线长度为$\frac{5}{6}d$。矩形的对角线的长度是一个矩形中的所有点之间的最长距离，而$\frac{5}{6}d<d$，而这个“日”字形中包含的所有原点集中的点之间的距离一定是大于等于d的，所以，每个$\frac{2}{3}d\times \frac{1}{2}d$的小矩形中，至多包含一个点，即整个“日”字形中最多只包含原点集中的6个点。这样不难证明，每个点对时间的贡献为常数级别，对中间“竖条”（“竖条”定义见上文）间点的最近距离的求解的时间复杂度为$O(n)$，排序需要$O(n\log n)$的时间，所以这个部分的总时间复杂度为$O(n\log n)$。

其实不必把“竖条”中midx左半部分的点与右半部分的点分开考虑，时间复杂度不变，因为每个点对答案的贡献仍为常数（与i出于midx同侧的点中再画一个“日”字形，里面的点数最多也只有6个，$2\times 6=12$）。因为这样写起来代码比较简单粗暴，所以我的代码中采用了这种写法。

代码及注释

注：这个代码是 2018 年的时候写的，当时比较懒，在合并的时候直接使用了 $sort$ 排序，这种做法时间复杂度为 $O(n{\lg }^{2}n)$，当时没指出来，也算是给自己留了个大坑吧。直到 2022 年我才把这个坑填了。

#include <cstdio>
#include <cmath>
#include <vector>
#include <algorithm>
using namespace std;

struct node {double x, y;}; /// 记录点坐标
bool same(double a, double b) { /// 1e-5精度意义下的浮点数相等
	if(fabs(a-b) <= 1e-5) return true; return false;
}
bool cmpx(node a, node b) { /// 以x为第一关键字排序
	if(!same(a.x, b.x)) return a.x<b.x; return a.y<b.y;
}
bool cmpy(node a, node b) { /// 以y为第一关键字排序
	if(!same(a.y, b.y)) return a.y<b.y; return a.x<b.x;
}

const int maxn = 200000 + 6; node arr[maxn]; /// arr 储存点的坐标
#define sqr(A) ((A)*(A))
double dist(node a, node b) { /// 求两点间距离
	return sqrt(sqr(a.x-b.x) + sqr(a.y-b.y));
}

double mind(int L, int R) {
	sort(arr+L, arr+R+1, cmpx); /// 按照x坐标排序以便分治
	double ans = 1e300; /// inf
	if(R-L+1 <= 3) { /// n<=3 暴力作，其实也可以不这么写
		for(int i = L; i <= R; i ++) { /// 也可以写成 n=2返回两点距离,n=1返回inf		
			for(int j = i+1; j <= R; j ++) {
				ans = min(ans, dist(arr[i], arr[j]));
			}
		}
	}else { /// 分治
		int mid = (L + R)/2; double midx = arr[mid].x; /// midx为中间分界线的横坐标
		ans = min(ans, mind(L,   mid));
		ans = min(ans, mind(mid+1, R)); /// 分治，ans即为上文中所说的d
		vector<node> avai; avai.clear(); /// 用vector存一下“竖条”中的点
		for(int i = L; i <= R; i ++) { /// 距离小于等于d（其实写小于也行）
			if(fabs(arr[i].x-midx) <= ans) avai.push_back(arr[i]);
		}
		double dnow = 1e300;
		sort(avai.begin(), avai.end(), cmpy); /// 按y排序
		for(int i = 0; i < avai.size(); i ++) {
			for(int j = i+1; j<avai.size(); j ++) {
				double d = dist(avai[i], avai[j]);
				if(d>ans && !same(d, ans)) break; 
				/// 及时break，y坐标之差大于d（写得很诡异，是为了避免精度误差的问题）
				dnow = min(dnow, d);
			}
		}
		ans = min(ans, dnow); avai.clear();
	}
	return ans;
}

int main() {
	int n; scanf("%d", &n);
	for(int i = 1; i <= n; i ++) scanf("%lf%lf", &arr[i].x, &arr[i].y); /// 输入点集
	double ans = mind(1, n); printf("%.4lf\n", ans); /// 输出答案
	return 0;
}

2022-03-23 补充 $O(n\lg n)$ 做法

时隔四年终于把这个坑填上了！！！

// 感觉从来都没写过最近点对问题的 O(nlgn) 做法
// 心血来潮，写一次


// Author: GGN_2015
// Date  : 2022-03-23


// 基本思想：在回归时进行归并排序 
// 从而保证合并在 O(n) 时间内完成 


#include <algorithm>
#include <cstdio>
#include <cmath>
using namespace std;


const int maxn = 100000 + 6;
const long long inf = 0x7f7f7f7f7f7f7f7fLL;


struct Point {int x, y;} ps[maxn];           // 用结构体储存所有的点坐标 


Point Ltmp[maxn], Rtmp[maxn];                // 临时数组 
int lcnt, rcnt;


bool cmpx(const Point& A, const Point& B) {  // 按照 x 坐标进行排序 
    return A.x != B.x ? A.x < B.x : A.y < B.y; 
}


long long sqr(int x) {                       // 计算平方（注意 long long） 
    return (long long)x * x;
}
long long dis(const Point& A, const Point& B) {
    return sqr(A.x - B.x) + sqr(A.y - B.y);  // 计算两点间距离的平方 
}


void merge(int L, int mid, int R) {          // 按照 y 坐标进行归并排序的合并操作 
    lcnt = 0;                                // 借用 Ltmp 临时数组进行归并排序 
    int i = L, j = mid + 1;                  // i, j 分别为左侧数组和右侧数组的 "当前元素" 
    while(i <= mid && j <= R) {
        if(ps[i].y != ps[j].y ? ps[i].y < ps[j].y : ps[i].x < ps[j].x) {
                                             // 按照 y 坐标从小到大排序 
            Ltmp[++ lcnt] = ps[i];
            i ++;
        }else {
            Ltmp[++ lcnt] = ps[j];
            j ++;
        }
    }
    while(i <= mid) {                        // 左侧数组中仍有剩余元素 
        Ltmp[++ lcnt] = ps[i];
        i ++;
    }
    while(j <= R) {                          // 右侧数组中仍有剩余元素 
        Ltmp[++ lcnt] = ps[j];
        j ++;
    }
    for(int i = 1; i <= lcnt; i ++) {        // 将临时数组中的数据拷贝回 ps 数组 
        ps[L + i - 1] = Ltmp[i];
    }
}


long long solve(int L, int R) {              // 递归计算区间 [L, R] 的最小距离，并将点按照 y 坐标排序 
    if(L >= R) return inf;                   // 空区间 / 只有一个节点的区间不需要计算 
    int mid  = (L + R) / 2;
    int midx = ps[mid].x;
    long long lans = solve(L,   mid);        // 递归计算左半区间和右半区间 
    long long rans = solve(mid+1, R);
    long long D = min(lans, rans);
    long long mindis = inf;
    lcnt = 0;
    for(int i = L; i <= mid; i ++) {         // 载入左半区间距中轴线距离 <= sqrt(mindis) 的点 
        if(sqr(midx - ps[i].x) <= D) {
            Ltmp[++ lcnt] = ps[i];
        }
    }
    rcnt = 0;
    for(int i = mid+1; i <= R; i ++) {       // 载入右半区间距中轴线距离 <= sqrt(mindis) 的点 
        if(sqr(ps[i].x - midx) <= D) {
            Rtmp[++ rcnt] = ps[i];
        }
    }
                                             // 注：Ltmp 和 Rtmp 中的数据是按照 Y 坐标有序的 
    int lpos = 1, rpos = 0;
    for(int i = 1; i <= lcnt; i ++) {        // 枚举 Ltmp 中的点的点 
        while(rpos < rcnt && 
            (Rtmp[rpos + 1].y < Ltmp[i].y || sqr(Rtmp[rpos + 1].y - Ltmp[i].y) <= D)) {
            rpos ++;
        }
        while(lpos < rcnt && Ltmp[i].y > Rtmp[lpos].y && sqr(Ltmp[i].y - Rtmp[lpos].y) > D) {
            lpos ++;
        }
        for(int j = lpos; j <= rpos; j ++) { // Rtmp[lpos .. rpos] 是 日字形中的点 
            mindis = min(mindis, dis(Ltmp[i], Rtmp[j]));
        }
    }
    merge(L, mid, R);                        // 归并排序的合并操作 
    return min(D, mindis);
}


int main() {
    int n; scanf("%d", &n);
    for(int i = 1; i <= n; i ++) {           // 输入所有点的坐标 
        scanf("%d%d", &ps[i].x, &ps[i].y);
    }
    sort(ps + 1, ps + n + 1, cmpx);          // 调了一下午发现忘排序了 ......
    long long ans = solve(1, n);             // 递归计算 
    printf("%.4lf\n", sqrt(ans));            // 输出最近点对距离 
    return 0;
}

2022-11-06 后记

和曦神鹏犇打完 $47$ 届 ICPC 沈阳站，$37$ 名，银牌第二，一起去日新楼吃饭，鹏犇请客。我们突然讨论到这道题，然后我时间复杂度的证明还给说错了。我后来仔细地想了一下，对于我现行的做法，应该把上面时间复杂度证明中的“日字形”横着画，才能更好的说明时间复杂度确实是 $O(6n)$。