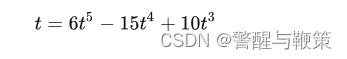柏林噪声(Perlin Noise) 介绍及应用

什么是噪声

信号处理中一般指原信号中不存在的无规则的额外信号。在处理过程中一般是我们不需要的，需要被处理掉的。噪声和信号本身无关，其频率和强弱变化无规律。

噪声有什么用处

就如上面提到的那样，噪声是干扰原信号的存在。在信号处理中，我们一般都希望通过各种方法将其从原信号中剥离出来并除掉。既然如此，为什么我们还需要创造出各式各样的噪声生成算法。原因很简单，就是我们自然界中存在各种各样的噪声。而当我们的程序出于某些目的想要模拟这些随机过程时（例如云朵，火焰等），我们就需要噪声了。

噪声可视化

我们用随机数算法产生的二维噪声图，如下图所示：

float random(in vec2 p){
    return fract(sin(dot(p.xy ,vec2(13.0,78.23))) * 51043.0123);
}

噪声图像

我们可以看到用随机函数生成的噪声纹理太过嘈杂，不像我们自然界中经常见到一些非常漂亮的噪声（像数目的纹理，石头的纹理，流水等）。因此，用这种噪声来模拟上述噪声难度太大了。这也是为什么图形学的先辈们想出各种各样其他噪声算法的原因。柏林噪声就是其中之一。

柏林噪声

柏林噪声属于基于晶格(Lattice based)的生成算法。在介绍柏林噪声算法之前，我们简单介绍下什么是晶格。以二维图像为例，晶格就是等分的网格，以一定单位将我们的图像划分成x*y（x行和y列）的网格。如下图，我们将图像划分成了3 * 3的网格。

晶格

当晶格数目越多时，生成的噪声将越“密集”。

下面来介绍柏林噪声的算法：
Perlin noise噪声生成算法总共有三个步骤：

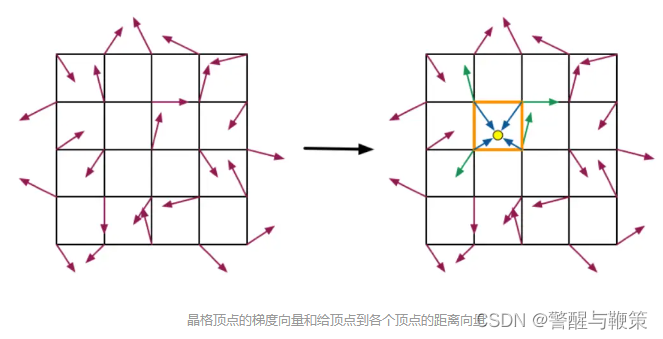
首先，定义一个晶格结构。晶格结构中的每个晶格顶点都有一个梯度向量。在二维的情况下，晶格结构是个平面的网格。在三维情况下，晶格结构是个立方体网络，以此类推。
其次，给定一个点（在二维情况下就是二维坐标。在三维情况下就是个三维坐标。）我们需要计算该点到该点所在的晶格顶点的距离向量，再分别乘以对应顶点的梯度向量，得到2n个点乘结果（n为空间下，每个晶格有2n个顶点）。
根据缓和曲线（ease curve）使用距离采样权重值用于最后插值。曲线方程为：s(t) = 3t2 - 2t3，后改良为s(t) = 6t5 - 15t4 + 10t3。

在这里对第三点插值权重值为什么不直接应用距离来算，即选择函数s(t) = t，来进行线性插值。因为我们的晶格长度都是单位长度，所以每个点到该点所处晶格顶点的距离是[0, 1]之间的数。而 s(t) = t 函数在 0 和 1 两点上的一阶导数不为 0（为1）。这样导致噪声变化的平滑程度加剧。而上述的s(t) = 3t2 - 2t3和s(t) = 6t5 - 15t4 + 10t3的一阶导数在0和1两点的倒数都为0。且s(t) = 6t5 - 15t4 + 10t3的二阶导数也满足在0和1两点为0。说明s(t) = 6t5 - 15t4 + 10t3函数不仅在0和1的斜率为零，且斜率本身的变化率也为0。所以在每个晶格顶点附近区域的变化过渡会更加的平滑。

上图是图片划分的晶格图。左边是晶格图以及相应每个晶格顶点上面梯度向量示意图。右边的绿色箭头是给定某个输入点（黄色）到该点所处晶格顶点的距离向量。
现在剩下的就是每个晶格顶点的梯度向量如何得到？
Perlin在他的实现中采用了以下方法（用二维为例）：
首先按之前的方法生成在单位正方形内随机梯度向量，然后剔除那些不在单位圆内的向量，直到找到了需要数目的随机梯度向量。Perlin把这些预计算得到的向量存储在一个查找表G[n]中，n是纹理大小，例如256 x 256大小的纹理对应n为256。虽然我们实际上需要n x n个梯度向量，这样会造成有些顶点的梯度是重复的。Perlin认为，重复是可以允许的，只要它们的间距够大就不会被察觉。因此，Perlin还预计算了一个随机排列数组P[n]，P[n]里面存储的是打乱后的0~n-1的排列值。这样一来，当我们想要得到(i, j)处晶格的梯度向量时，可以使用：
G = G[(i + P[j])mod n]。

一维柏林噪声

3.1. 初始化

在初始化排列表和梯度表之前，我们先了解一下它们的作用。排列表是一个乱序存放一系列索引值的表，而梯度表是一个存放了一系列随机梯度值的表，两者都具有很强的随机性。在决定一个点的梯度时，需要结合哈希函数，以点的坐标为参数，利用所得的值作为索引，去排列表中取对应的值。所取得的排列表中的值，就是该点在梯度表中对应梯度值的索引。这样解释可能会有些让人摸不着头脑，我们来看一段伪代码。

// 排列表
int[] perm = {...};

// 梯度表
float[] grad = {...};

// 只有整数点才需要随机指定梯度，以计算非整数点的插值
void Hash(ref int[] gradient, int x, int y) {
    // 通过哈希函数找到排列表的索引
    int permIdx[] = new int[2];
    permIdx[0] = FindIndex(x);
    permIdx[1] = FindIndex(y);

    // 通过排列表索引找到梯度表的索引
    int gradIdx[] = new int[2];
    gradIdx[0] = perm[permIdx[0]];
    gradIdx[1] = perm[permIdx[1]];

    // 在梯度表中找到梯度值
    gradient[0] = grad[gradIdx[0]];
    gradient[1] = grad[gradIdx[1]];
}

这段代码以二维柏林噪声为例，描述了确定一个点梯度值的过程。梯度表中的值都是随机生成的，通过对点的 x 和 y 坐标分别进行计算，可以得到点的梯度（即一个二维向量）。确定一点的梯度值并不止这一种方法，另一种可行方法之后会提到。

在一维柏林噪声中，各个整点的梯度就是斜率，所以我们可以不依赖梯度表，将排列表中所取到值直接作为梯度即可。因为排列表中的值是乱序的，所以有良好的随机性，且对于同样的输入，它的输出都相同，伪随机性也得以保留。在Ken Perlin的经典噪声算法中，使用的排列表是由数字0到255散列组成的。

// Language: Processing
// Permutation table
static int[] perm = {151,160,137,91,90,15,
 131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23,
 190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
 88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
 77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
 102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
 135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
 5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
 223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
 129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
 251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
 49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
 138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180};

3.2. 采样和插值

之前提到，一维柏林噪声的采样空间是一个一维坐标轴，那么一维柏林噪声函数的参数就是坐标轴上的一点，其参考点就是它左右两侧最近的整数点。首先，我们需要找到这两个点，并求出它们对应的梯度以及相对输入点的方向向量。

图2 一维噪声插值

至此，一个柏林噪声生成算法的所有元素都已经具备，我们用每个点梯度值乘以其方向向量，这个值为该店对输入点灰度值的影响，带入插值公式求得输入点的灰度值。

float perlin(float x) {
    // 整数x1和x2的坐标
    int x1 = floor(x);
    int x2 = x1 + 1;

    // x1和x2的梯度值
    float grad1 = perm[x1 % 255] * 2.0 - 255.0;
    float grad2 = perm[x2 % 255] * 2.0 - 255.0;
    // x1和x2指向x的方向向量
    float vec1 = x - x1;
    float vec3 = x - x2;

    // x到x1的距离即vec1，利用公式3计算平滑参数
    float t = 3 * pow(vec1, 2) - 2 * pow(vec1, 3);

    // 梯度值与方向向量的乘积
    float product1 = grad1 * vec1;
    float product2 = grad2 * vec2;

    // 插值
    return product1 + t * (product2 - product1);
}

3.3. 结果

图3 一维柏林噪声

4. 二维柏林噪声

4.1. 初始化

在这一部分，为了简单，我没有预计算梯度表，然后通过排列表去索引梯度值，而是选择了舍弃排列表，为每个点随机计算一个梯度值。

Ken Perlin 在后来的改进版算法中提到，由于（在三维柏林噪声中）立方体本身具有方向性偏差（立方体中的点指向立方体顶点的向量相对指向边或面上一点的向量来说，会被拉长）。这种偏差会使噪声图上出现零星的聚集现象（某些点的灰度值异常的高）。于是他改用了一组服从均匀分布的向量，利用排列表来随机选取，他认为排列表的随机性已经足够。所以，我们舍弃排列表的随机性，选择随机的梯度值也算是有理可循。

要针对一个二维的点产生一个二维的随机向量，需要常用于着色器的随机数生成函数 hash22。

float[] grad(float x, float y) {
   float[] vec = new float[2];
   vec[0] = x * 127.1 + y * 311.7;
   vec[1] = x * 269.5 + y * 183.3;

   float sin0 = sin(vec[0]) * 43758.5453123;
   float sin1 = sin(vec[1]) * 43758.5453123;
   vec[0] = (sin0 - floor(sin0)) * 2.0 - 1.0;
   vec[1] = (sin1 - floor(sin1)) * 2.0 - 1.0;

    // 归一化，尽量消除正方形的方向性偏差
   float len = sqrt(vec[0] * vec[0] + vec[1] * vec[1]);
   vec[0] /= len;
   vec[1] /= len;

   return vec;
}

4.2. 采样和插值

现在我们知道，在二维柏林噪声中，采样空间是一个二维坐标系，坐标系被横纵坐标均为整数的点划分为无数个如下图所示的晶格（Lattice）。输入点插值的参考点为形成包围它的单位正方形的四个点。求参考点坐标很简单，先对P点坐标进行向下取整得到P0点，因为都是整数坐标点，求其它三个点只需要简单的加法，这里就不列出公式了。

图4 二维噪声插值

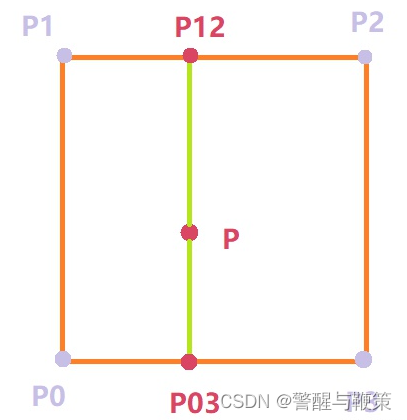
方向向量的求解和一维的情况一样，只不过涉及两个变量。梯度向量由随机计算得来，算法也已经讨论了，这些就都不再说了，这里主要来看一下如何求解二维情况下的插值。看到上面这张图，我想读者心里已经有个大概了。实际上，二维的插值求解和一维本质上也没有区别，只不过需要求解三次：首先，对 P0 和 P3 求解插值得到 P03 ，再对 P1 和 P2 求解插值得到 P12 ，最后对 P03 和 P12 求解插值得到 P。是不是很简单？那么，我也想你现在应该也已经知道三维情况下如何求解了。没错，进行七次一维插值求解即可！

4.3. 晶格与噪声图

或许，你会想问晶格和噪声图到底是什么关系，这一点实际上非常重要，它关系到在一定分辨率下能否生成优质的柏林噪声图。晶格中的一点就是噪声图上一点吗？我们先来看下面这张图。

图5 晶格和噪声图

让我们把注意力放在红点上。显然，红点在晶格上的坐标大概是 (3.5,3.5) ，而在噪声图上的坐标差不多是 (175,175) （这张图的分辨率为 400×400 ）。所以，晶格上的点并不是噪声图上的点，而是对应噪声图上的一个像素，这个点的值就是对应像素的灰度值。这些和生成高质量的噪声图又有什么关系呢？

如果我们想向图片的某一个像素写入灰度值，我们必须得到对应的晶格中的点，并进行灰度值计算。想要得到对应的晶格中的点，最佳实践就是像上图一样，将晶格完整的覆盖一张图，这样才能通过像素坐标映射到晶格坐标。同时，读者还需自行决定将整个图片分成多少个晶格。晶格的个数根据图片像素来决定，才能达到最好的效果。。

float perlin() {
   int p0x = floor(x); // P0坐标
   int p0y = floor(y);
   int p1x = p0x;      // P1坐标
   int p1y = p0y + 1;
   int p2x = p0x + 1;  // P2坐标
   int p2y = p0y + 1;
   int p3x = p0x + 1;  // P3坐标
   int p3y = p0y;

   float g0x = grad(p0x, p0y)[0];  // P0点的梯度
   float g0y = grad(p0x, p0y)[1];
   float g1x = grad(p1x, p1y)[0];  // P1点的梯度
   float g1y = grad(p1x, p1y)[1];
   float g2x = grad(p2x, p2y)[0];  // P2点的梯度
   float g2y = grad(p2x, p2y)[1];
   float g3x = grad(p3x, p3y)[0];  // P3点的梯度
   float g3y = grad(p3x, p3y)[1];

   float v0x = x - p0x;  // P0点的方向向量
   float v0y = y - p0y;
   float v1x = x - p1x;  // P1点的方向向量
   float v1y = y - p1y;
   float v2x = x - p2x;  // P2点的方向向量
   float v2y = y - p2y;
   float v3x = x - p3x;  // P3点的方向向量
   float v3y = y - p3y;

   float product0 = g0x * v0x + g0y * v0y;  // P0点梯度向量和方向向量的点乘
   float product1 = g1x * v1x + g1y * v1y;  // P1点梯度向量和方向向量的点乘
   float product2 = g2x * v2x + g2y * v2y;  // P2点梯度向量和方向向量的点乘
   float product3 = g3x * v3x + g3y * v3y;  // P3点梯度向量和方向向量的点乘

   // P1和P2的插值
   float d0 = x - p0x;
   float t0 = 6.0 * pow(d0, 5.0) - 15.0 * pow(d0, 4.0) + 10.0 * pow(d0, 3.0);
   float n0 = product1 * (1.0 - t0) + product2 * t0;

   // P0和P3的插值
   float n1 = product0 * (1.0 - t0) + product3 * t0;

   // P点的插值
   float d1 = y - p0y;
   float t1 = 6.0 * pow(d1, 5.0) - 15.0 * pow(d1, 4.0) + 10.0 * pow(d1, 3.0);
   return n1 * (1.0 - t1) + n0 * t1;
}

void drawPerlin() {
    for(int i = 0; i < width; i ++) {
        for(int j = 0; j < height; j++) {
            // 将[-1, 1]的柏林噪声值映射到[0, 255]的灰度值
            float gray = map(perlin(tx, ty), -1, 1, 0, 255);
            noStroke();
            fill(gray);
            rect(i, j, 1, 1);
            // 图片像素为512x512，晶格数为16x16，将像素坐标映射到晶格坐标
            ty = ((j + 1.0) / height) * 16.0;
        }
        tx = ((x + 1.0) / width) * 16.0;
        ty = 0;
    }
}

4.4. 结果

这张图的像素为 400×400 ，被划分成了 16×16 晶格。

图6 二维柏林噪声，晶格数为16x16

作为对比，我们再生成一张同样像素的图，这次划分为 8×8 个晶格（原来的 14 ）。

图7 二维柏林噪声，晶格数为8x8

仔细观察你会发现，后者是前者左上角的一部分（在Processing中，画布的坐标原点在左上角， y 轴正方向向下）！换句话说，晶格数变为原来的 14 ，所生成的噪声图也是原来的 14 。现在我们知道，一张噪声图，图的像素数定义了图的大小，划分晶格的数量决定了噪声的范围，两者搭配使用，就可以实现想要的效果。

5. 三维柏林噪声

Ken Perlin 的柏林噪声的算法进行了改进：为了尽量规避立方体的方向性偏差，他不再使用随机梯度表，而是采用一组服从均匀分布的梯度向量，然后通过排列表进行索引，丢弃了梯度表的随机性，只依赖于排列表的随机性。这一组向量一共12个，是立方体中心点指向十二条边中心点的向量：

(1,1,0), (−1,1,0), (1,−1,0), (−1,−1,0),

(1,0,1), (−1,0,1), (1,0,−1), (−1,0,−1),

(0,1,1), (0,−1,1), (0,1,−1), (0,1,−1)

通过哈希函数，找到点对应的排列表中的值，再对12取余，即可得到这组向量其中一个的索引。

int index = perm[x + perm[y]] % 12;
float[] g = grad[index];

Stefan Gustavson 在一篇关于 Simplex噪声 的文章中提到，对于二维的柏林噪声也存在相同的处理方法：在单位圆上对称的选择8个或者16个向量存入梯度向量表，再通过排列表和哈希函数进行索引。

除此之外，如果你阅读了本文的代码，你会发现在二维柏林噪声中，我们用到的缓动曲线并不是公式4，而是一个新的缓动曲线公式：

因为，原公式的二阶导 6−12t在 t=0 或者 t=1 时均不等于0。当一个物体使用噪声置换贴图（Noise Displacement Map）时，这个非零性质会在其表面形成不连续的现象，让物体表面看起来好像被划分成一个一个的正方形了(如图8所示）。为什么会这样？我的理解如下： t=0 和 t=1 在晶格上是整数点的位置，一个整数点被同一个横排两个相邻的晶格所共用。对于左边的晶格该点 t=1 ，而对于右边的晶格该点 t=0 。但由于二阶导不连续，所以在取到这个点时，左右两边会有冲突，于是乎造成了这种不连续的现象。

图8 如果你仔细看，应该能看到表有些不自然的痕迹

6. 总结

柏林噪声的生成算法其实并没有那么难，主要经历以下三个步骤：

对排列表和梯度表进行初始化，梯度表可以不必随机生成，选择单位圆（球）上的对称的梯度向量也可。一维向量可以不用梯度表，直接用排列表中的值进行映射也能达到效果。
对于噪声图上的像素，找到它在晶格上对应的一点，并求出它的参考点的坐标。在一维情况下，参考点为两侧最近的整数点；二维情况下，参考点为组成包围该点的单位正方体的四个点；三维情况下，参考点为组成包围该点的单位立方体的八个点。需要注意的一点是，晶格必须与图片对齐且完全覆盖，否则坐标映射会很麻烦。
根据参考点的方向向量和梯度向量，并结合缓动曲线，求解最终的灰度值。一维噪声只需一次插值，二维需要三次插值，三维需要七次插值，呈指数增长，所以算法的时间复杂度是。

参考

^a bImproving noise, Ken Perlin https://mrl.nyu.edu/~perlin/paper445.pdf
^Simplex noise demystified, Stefan Gustavson http://webstaff.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf

噪声的分类
根据wiki，由程序产生噪声的方法大致可以分为两类：

类别   名称
基于晶格的方法（Lattice based）   又可细分为两种：
第一种是梯度噪声（Gradient noise），包括Perlin噪声， Simplex噪声，Wavelet噪声等；
第二种是Value噪声（Value noise）。
基于点的方法（Point based）   Worley噪声

需要注意的是，一些文章经常会把Perlin噪声、Value噪声与分形噪声（Fractal noise）弄混，这实际在概念上是有些不一样的。分形噪声会把多个不同振幅、不同频率的octave相叠加，得到一个更加自然的噪声。而这些octave则对应了不同的来源，它可以是Gradient噪声（例如Perlin噪声）或Value噪声，也可以是一个简单的白噪声（White noise）。

一些非常出色的文章也错误把这种分形噪声声称为Perlin噪声，例如：

Hugo Elias的文章，这篇文章讲得挺有趣的，关于什么是octave、怎么混合它们都讲得很细致，也非常有名，但作者错误地把值噪声+分形噪声标识为Perlin噪声，他的文章链接也出现了wiki的值噪声（Value noise）的页面中。

Devmag的如何在你的游戏中使用Perlin噪声一文，同样非常有名，但同样错误地把白噪声+分形噪声认为是Perlin噪声。

如果读者常逛shadertoy的话，会发现很多shader使用了类似名为fbm的噪声函数。fbm实际就是分型布朗运动（Fractal Brownian Motion）的缩写，读者可以把它等同于我们上面所说的分形噪声（Fractal noise），我们以下均使用fbm来表示这种噪声的计算方法。如果要通俗地说fbm和之前提及的Perlin噪声、Simplex噪声、Value噪声、白噪声之间的联系，我们可以认为是很多个不同频率、不同振幅的基础噪声（指之前提到的Perlin噪声、Simplex噪声、Value噪声、白噪声等之一）之间相互叠加，最后形成了最终的分形噪声。这里的频率指的是计算噪声时的采样距离，例如对于基于晶格的噪声们，频率越高，单位面积（特指二维）内的晶格数目越多，看起来噪声纹理“越密集”；而振幅指的就是噪声的值域。下图显示了一些基础噪声和它们fbm后的效果：

说明：分割线左侧表示单层的基础噪声，右侧表示通过叠加不同频率噪声后的fbm效果。上面效果来源于shadertoy：Perlin噪声，Simplex噪声，Value噪声，Worley噪声。

由于Worley噪声的生成和其他噪声有明显不同，因此不是本文的重点。它主要用于产生孔状的噪声，有兴趣的读者可以参见偶像iq的文章：

http://www.iquilezles.org/www/articles/smoothvoronoi/smoothvoronoi.htm
http://www.iquilezles.org/www/articles/voronoise/voronoise.htm
Perlin噪声、Simplex噪声和Value噪声在性能上大致满足：Perlin噪声 > Value噪声 > Simplex噪声，Simplex噪声性能最好。Perlin噪声和Value噪声的复杂度是O(2n)
�
(
2
�
)
，其中n是维数，但Perlin噪声比Value噪声需要进行更多的乘法（点乘）操作。而Simplex噪声的复杂度为O(n2)
�
(
�
2
)
，在高纬度上优化明显。

下面的内容就是重点解释Perlin噪声、Perlin噪声和Simplex噪声这三种常见的噪声，最后再介绍fbm。

Perlin噪声
先介绍大名鼎鼎的Perlin噪声。很多人都知道，Perlin噪声的名字来源于它的创始人Ken Perlin。Ken Perlin早在1983年就提出了Perlin noise，当时他正在参与制作迪士尼的动画电影《电子世界争霸战》（英语：TRON），但是他不满足于当时计算机产生的那种非常不自然的纹理效果，因此提出了Perlin噪声。随后，他在1984年的SIGGRAPH Course上做了名为Advanced Image Synthesis1的课程演讲，并在SIGGRAPH 1985上发表了他的论文2。由于Perlin噪声的算法简单，被迅速应用到各种商业软件中。我们这位善良的Perlin先生却并没有对Perlin噪声算法申请专利（他说他的祖母曾叫他这么做过……），如果他这么做了那会是多大一笔费用啊！（不过在2001年的时候，旁人看不下去了，把三维以上的Simplex噪声的专利主动授予了Perlin。对，Simplex噪声也是人家提出的……）再后来Perlin继续研究程序纹理的生成，并和他的一名学生又在SIGGRAPH 1989上发表了一篇文章3，提出了超级纹理（hypertexture）。他们使用噪声+fbm+ray marching实现了各种有趣的效果。到1990年，已经有大量公司在他们的产品中使用了Perlin噪声。在1999年的GDCHardCore大会上，Ken Perlin做了名为Making Noise的演讲4，系统地介绍了Perlin噪声的发展、实现细节和应用。如果读者不想读论文的话，强烈建议你看一下Perlin演讲的PPT。

后来在2002年，Perlin又发表了一篇论文5来改进原始的Perlin噪声中的一些问题，例如原来的缓和曲线s(t)=3t2−2t3
�
(
�
)
=
3
�
2
−
2
�
3
的二阶导6−12t
6
−
12
�
在t=0
�
=
0
和t=1
�
=
1
时均不等于0，这使得在相邻的晶格处它们的二阶导并不连续。因此Perlin提出使用一个更好的缓和曲线s(t)=6t5−15t4+10t3
�
(
�
)
=
6
�
5
−
15
�
4
+
10
�
3
；此外还改进了晶格顶点处随机梯度向量的选取。有兴趣的读者可以参考：

Perlin在2002年发表的论文：http://mrl.nyu.edu/~perlin/paper445.pdf
GPU Gems的文章：http://http.developer.nvidia.com/GPUGems/gpugems_ch05.html
GPU Gems 2的文章：http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter26.html
后面只介绍原始Perlin噪声的实现。

实现
Perlin噪声还是比较简单的，在1983年的计算机上实现的算法也不允许对计算量、内存有多大的要求。概括来说，Perlin噪声的实现需要三个步骤：

定义一个晶格结构，每个晶格的顶点有一个“伪随机”的梯度向量（其实就是个向量啦）。对于二维的Perlin噪声来说，晶格结构就是一个平面网格，三维的就是一个立方体网格。
输入一个点（二维的话就是二维坐标，三维就是三维坐标，n维的就是n个坐标），我们找到和它相邻的那些晶格顶点（二维下有4个，三维下有8个，n维下有2n
2
�
个），计算该点到各个晶格顶点的距离向量，再分别与顶点上的梯度向量做点乘，得到2n
2
�
个点乘结果。
使用缓和曲线（ease curves）来计算它们的权重和。在原始的Perlin噪声实现中，缓和曲线是s(t)=3t2−2t3
�
(
�
)
=
3
�
2
−
2
�
3
，在2002年的论文6中，Perlin改进为s(t)=6t5−15t4+10t3
�
(
�
)
=
6
�
5
−
15
�
4
+
10
�
3
。这里简单解释一下，为什么不直接使用s(t)=t
�
(
�
)
=
�
，即线性插值。直接使用的线性插值的话，它的一阶导在晶格顶点处（即t = 0或t = 1）不为0，会造成明显的不连续性。s(t)=3t2−2t3
�
(
�
)
=
3
�
2
−
2
�
3
在一阶导满足连续性，s(t)=6t5−15t4+10t3
�
(
�
)
=
6
�
5
−
15
�
4
+
10
�
3
在二阶导上仍然满足连续性。
我们下面以二维的为例，再详细解释一下。我们可以用下面的图来表示上面的第一步和第二步：

一个问题是晶格顶点处的伪随机梯度向量是如何得到的，当然我们可以通过random这样的函数来计算单位正方形（二维）内的x和y分量值，但我们更愿意要那些在单位圆内的梯度向量。Perlin在他的实现中选择使用蒙特卡洛模拟方法来选取这些随机梯度向量。具体方法是（我把描述适应到了二维）：首先按之前的方法生成在单位正方形内随机梯度向量，然后剔除那些不在单位圆内的向量，直到找到了需要数目的随机梯度向量。Perlin把这些预计算得到的向量存储在一个查找表G[n]中，n是纹理大小，例如256 x 256大小的纹理对应n为256。虽然我们实际上需要n x n个梯度向量，这样会造成有些顶点的梯度是重复的。Perlin认为，重复是可以允许的，只要它们的间距够大就不会被察觉。因此，Perlin还预计算了一个随机排列数组P[n]，P[n]里面存储的是打乱后的0~n-1的排列值。这样一来，当我们想要得到(i, j)处晶格的梯度向量时，可以使用：

G=G[(i+P[j])mod n]
�
=
�
[
(
�
+
�
[
�
]
)
�
�
�

�
]
得到了梯度后，我们就可以进行点乘，得到4个点乘结果，然后使用缓和曲线对它们进行插值即可。这里使用的权重就是输入点到4个顶点的横纵距离。

在原始的Perlin噪声实现中，Perlin对梯度向量的选择一般是取单位圆（三维就是单位球）内一些不同方向的向量。在他后面的改进算法7中，Perlin建议把三维的梯度向量初始化为到立方体12条边的向量值，来保证各个方向之间的不关联性。

可以看出，Perlin噪声算法的时间复杂度为O(2n)
�
(
2
�
)
（n是维数），2n
2
�
其实就是每个晶格的顶点个数，对于每个输入点我们需要进行这么多次的点乘操作。因此，随着维数的增大，例如计算三维四维的Perlin噪声，时间会迅速增加。Perlin在2002年介绍了他优化后的一种噪声——Simplex噪声，这种噪声的复杂度是O(n2)
�
(
�
2
)
，在高纬度上时间优化明显，我们后面会讲到这种噪声。

效果
Shadertoy上有很多关于Perlin噪声的实现，我也山寨了一个：

它的主要代码如下：

vec2 hash22(vec2 p)
{
p = vec2( dot(p,vec2(127.1,311.7)),
dot(p,vec2(269.5,183.3)));

return -1.0 + 2.0 * fract(sin(p)*43758.5453123);
}
float perlin_noise(vec2 p)
{
vec2 pi = floor(p);
vec2 pf = p - pi;

vec2 w = pf * pf * (3.0 - 2.0 * pf);

return mix(mix(dot(hash22(pi + vec2(0.0, 0.0)), pf - vec2(0.0, 0.0)),
dot(hash22(pi + vec2(1.0, 0.0)), pf - vec2(1.0, 0.0)), w.x),
mix(dot(hash22(pi + vec2(0.0, 1.0)), pf - vec2(0.0, 1.0)),
dot(hash22(pi + vec2(1.0, 1.0)), pf - vec2(1.0, 1.0)), w.x),
w.y);
}
这里的实现实际是简化版的，我们在算梯度的时候直接取随机值，而没有归一化到单位圆内。

上图包含了四种噪声组合，这也是Perlin在1999年的GDC上做演讲时采用的一个示例，不过Perlin的例子是三维的，而且添加了光照等计算。

左上角的部分。这是最简单的单独的Perlin噪声，它的噪声模拟如下：

float noise_itself(vec2 p)
{
return noise(p * 8.0);
}
上面的代码在整个屏幕上模拟了一个8 x 8的网格结构。在绘制时，我们只需要将一个深蓝色乘以噪声即可得到类似的效果。

单独一个Perlin噪声虽然也有一定用处，但是效果往往很无趣。因此，Perlin指出可以使用不同的函数组合来得到更有意思的结果，这些函数组合通常就是指通过分形叠加（fractal sum），也就是我们之前说的fbm。

左下角的部分。这个部分使用了fbm进行叠加来形成一个分形噪声。公式如下：
noise(p)+12noise(2p)+14noise(4p)+...
�
�
�
�
�
(
�
)
+
1
2
�
�
�
�
�
(
2
�
)
+
1
4
�
�
�
�
�
(
4
�
)
+
.
.
.
即每一次噪声的采样频率翻倍，而振幅减少一倍。很多文章错误地把这种计算认为是Perlin噪声，这是不对的。Perlin噪声只是对应了其中每一个octave。代码是：

float noise_sum(vec2 p)
{
float f = 0.0;
p = p * 4.0;
f += 1.0000 * noise(p); p = 2.0 * p;
f += 0.5000 * noise(p); p = 2.0 * p;
f += 0.2500 * noise(p); p = 2.0 * p;
f += 0.1250 * noise(p); p = 2.0 * p;
f += 0.0625 * noise(p); p = 2.0 * p;

return f;
}
上面叠加了5层，并把初始化采样距离设置为4，这都是可以自定义的。这种噪声可以用来模拟石头、山脉这类物体。

右下角的部分。这一部分只是在上一部分进行了一点修改，对噪声返回值进行了取绝对值操作。它使用的公式如下：

|noise(p)|+12|noise(2p)|+14|noise(4p)|+...
|
�
�
�
�
�
(
�
)
|
+
1
2
|
�
�
�
�
�
(
2
�
)
|
+
1
4
|
�
�
�
�
�
(
4
�
)
|
+
.
.
.
它对应的代码如下：

float noise_sum_abs(vec2 p)
{
float f = 0.0;
p = p * 7.0;
f += 1.0000 * abs(noise(p)); p = 2.0 * p;
f += 0.5000 * abs(noise(p)); p = 2.0 * p;
f += 0.2500 * abs(noise(p)); p = 2.0 * p;
f += 0.1250 * abs(noise(p)); p = 2.0 * p;
f += 0.0625 * abs(noise(p)); p = 2.0 * p;

return f;
}
由于进行了绝对值操作，因此会在0值变化处出现不连续性，形成一些尖锐的效果。通过合适的颜色叠加，我们可以用这种噪声来模拟火焰、云朵这些物体。Perlin把这个公式称为turbulence（湍流？），因为它看起来挺像的。

右上角的部分。这个部分是在之前turbulence公式的基础上使用了一个关于表面x分量的正弦函数：

sin(x+|noise(p)|+12|noise(2p)|+14|noise(4p)|+...)
�
�
�
(
�
+
|
�
�
�
�
�
(
�
)
|
+
1
2
|
�
�
�
�
�
(
2
�
)
|
+
1
4
|
�
�
�
�
�
(
4
�
)
|
+
.
.
.
)
这个公式可以让表面沿着x方向形成一个条纹状的结构。Perlin使用这个公式模拟了一些大理石材质。我们的代码如下：

float noise_sum_abs_sin(vec2 p)
{
float f = 0.0;
p = p * 7.0;
f += 1.0000 * abs(noise(p)); p = 2.0 * p;
f += 0.5000 * abs(noise(p)); p = 2.0 * p;
f += 0.2500 * abs(noise(p)); p = 2.0 * p;
f += 0.1250 * abs(noise(p)); p = 2.0 * p;
f += 0.0625 * abs(noise(p)); p = 2.0 * p;
f = sin(f + p.x/32.0);

return f;
}
我们可以通过改变x分量前面的系数来控制条纹的疏密。

以上，我们就演示了基本的Perlin噪声的实现。Perlin在1999年Making Noise的演讲8中，还介绍了如何使用噪声来控制纹理动画。他指出，想要一个二维的turbulence纹理动画（例如云、火焰等），我们需要使用三维的噪声，其中第三维对应了时间变量。Shadertoy上有很多这样的例子，例如下面的就是模拟了Perlin演讲中实现的火球效果：

width="500" height="320" src="https://www.shadertoy.com/embed/lsf3RH?gui=true&t=10&paused=false&muted=false" allowfullscreen="">
有兴趣的可以尝试实现Perlin演讲中实现的云彩飘动效果。

Value噪声
在理解了Perlin噪声的实现后，Value噪声就很简单了。它把原来的梯度替换成了一个简单的伪随机值，我们也不需要进行点乘操作，而直接把晶格顶点处的随机值按权重相加即可。

实现
和Perlin噪声一样，它也是一种基于晶格的噪声，也需要三个步骤：

定义一个晶格结构，每个晶格的顶点有一个“伪随机”的值（Value）。对于二维的Value噪声来说，晶格结构就是一个平面网格，三维的就是一个立方体网格。
输入一个点（二维的话就是二维坐标，三维就是三维坐标，n维的就是n个坐标），我们找到和它相邻的那些晶格顶点（二维下有4个，三维下有8个，n维下有2n
2
�
个），得到这些顶点的伪随机值。
使用缓和曲线（ease curves）来计算它们的权重和。同样，缓和曲线可以是s(t)=3t2−2t3
�
(
�
)
=
3
�
2
−
2
�
3
，也可以是s(t)=6t5−15t4+10t3
�
(
�
)
=
6
�
5
−
15
�
4
+
10
�
3
（如果二阶导不连续对效果影响较大时）。
Value噪声比Perlin噪声的实现更加简单，并且需要的乘法和加法操作也更少，它只需要得到晶格顶点的随机值再把它们按权重相加即可。

效果
我们再次使用之前在Perlin噪声效果展示时使用的代码，但改变一些参数就可以得到下面的效果：

它的主要代码如下：

float value_noise(vec2 p)
{
vec2 pi = floor(p);
vec2 pf = p - pi;

vec2 w = pf * pf * (3.0 - 2.0 * pf);

return mix(mix(hash21(pi + vec2(0.0, 0.0)), hash21(pi + vec2(1.0, 0.0)), w.x),
mix(hash21(pi + vec2(0.0, 1.0)), hash21(pi + vec2(1.0, 1.0)), w.x),
w.y);
}
1
2
3
4
5
6
7
8
9
10
11
可以看出，单独的Value噪声（左上角）会有很明显的像素块效果。其实我认为，当把Value噪声纹理的大小调的很大时，它近似就是一张白噪声纹理。不过所幸的是，在通过fbm叠加后，形成的分形噪声效果还是可以接受的，这也是为什么它会被大量应用在很多程序中来代替基于梯度的Perlin噪声。

Simplex噪声
最后，我们来介绍本文最难理解的一种噪声。在2001年SIGGRAPH Course上，Ken Perlin进行了一次演讲9，他介绍了对Perlin噪声的一个改进版噪声——Simplex噪声。感兴趣的读者可以看一下Perlin原版的Course Note。我们之前提到过很多次，Simplex噪声的计算复杂度为O(n2)
�
(
�
2
)
，优于Perlin噪声的O(2n)
�
(
2
�
)
。而且在效果上，Simplex噪声也克服了经典的Perlin噪声在某些视觉问题。但Simplex噪声的问题在于，它比较难理解，以至于当Perlin提出了后好几年的时间里它并没有被广泛使用。

实现
Simplex噪声也是一种基于晶格的梯度噪声，它和Perlin噪声在实现上唯一不同的地方在于，它的晶格并不是方形（在2D下是正方形，在3D下是立方体，在更高纬度上我们称它们为超立方体，hypercube），而是单形，simplex。那么什么是单形呢？

通俗解释单形的话，可以认为是在N维空间里，选出一个最简单最紧凑的多边形，让它可以平铺整个N维空间。我们可以很容易地想到一维空间下的单形是等长的线段（1-单形），把这些线段收尾相连即可铺满整个一维空间。在二维空间下，单形是三角形（2-单形），我们可以把等腰三角形连接起来铺满整个平面。三维空间下的单形，即3-单形就是四面体。更高维空间的单形也是存在的。

那么使用单形有什么好处呢？这可以从之前对单形的解释看出来——它的顶点数很少，要远小于超立方体（hypercube）的顶点个数。总结起来，在N维空间下，超立方体的顶点数目是2n
2
�
，而单形的顶点数目是n+1
�
+
1
，这使得我们在计算梯度噪声时可以大大减少需要计算的顶点权重数目。

在理解了单形后，Simplex噪声的计算过程其实和Perlin噪声基本一样。我们以二维空间下的为例。二维空间下的单形即是等边三角形，如下图所示。这些单形组成了一个单形网格结构，和Perlin噪声类似，这些网格顶点处也存储了伪随机梯度向量。

当输入一点后，我们找到该点所在的三角形（图中红色三角形），再找到该三角形三个顶点的梯度向量和每个顶点到输入点的差值向量，把每个顶点的梯度向量和插值向量做点乘，得到三个点乘结果。最后，我们把它们按权重进行叠加混合，这个权重与输入点到每个顶点的有关，即每个顶点的噪声贡献度为：

(r2−|dist|2)4×dot(dist,grad)
(
�
2
−
|
�
�
�
�
|
2
)
4
×
�
�
�
(
�
�
�
�
,
�
�
�
�
)
其中，dist
�
�
�
�
是输入点到该顶点的距离向量，grad
�
�
�
�
是该点存储的伪随机梯度向量，r2
�
2
的取值是0.5或0.6。取0.5时可以保证没有不连续的间断点，在连续性并不那么明显时可以取0.6得到更好的视觉效果。在Perlin原始的论文中，r的取值是0.6（后面我们会讲到0.5的值是如何得到的）。当得到单形每个顶点的噪声贡献度后，就可以把它们相加起来。为了把结果归一到-1到1的范围，我们往往还需要在最后乘以一个系数，这个系数值我们之后会讲到。

可以看出，Simplex噪声的实现过程和Perlin几乎完全一样。但是，在上面的实现中我们始终忽略了一个问题，就是如何找到输入点所在的单形？在计算Perlin噪声时，判断输入点所在的正方形是非常容易的，我们只需要对输入点下取整即可找到，那么这里能不能也这么计算呢？幸运的是，数学家们已经为我们解决了这个问题：我们可以把单形进行坐标偏斜（skewing），把平铺空间的单形变成一个新的网格结构，这个网格结构是由超立方体组成的，而每个超立方体又由一定数量的单形构成。听不懂是不是？2005年Stefan的一篇论文10里的一张图大概可以解救你！

我们之前讲到的单形网格如上图中的红色网格所示，它们有一些等边三角形组成（注意到这些等边三角形是沿空间对角线排列的）。经过坐标倾斜后，它们变成了后面的黑色网格，这些网格由正方形组成，每个正方形是由之前两个等边三角形变形而来的三角形组成。这个把N维空间下的单形网格变形成新网格的公式如下：

x′=x+(x+y+...)⋅K1y′=y+(x+y+...)⋅K1...其中，K1=n+1−−−−−√−1n
�
′
=
�
+
(
�
+
�
+
.
.
.
)
⋅
�
1
�
′
=
�
+
(
�
+
�
+
.
.
.
)
⋅
�
1
.
.
.
其
中
，
�
1
=
�
+
1
−
1
�
在二维空间下，取n为2即可。这样变换之后，我们就可以按照之前方法判断该点所在的超立方体，在二维下即为正方形。这样我们就有了Simplex噪声的第一步：

1 坐标偏斜：把输入点坐标进行坐标偏斜，对坐标下取整得到输入点所在的超立方体xi=floor(x′),yi=floor(y′),...
�
�
=
�
�
�
�
�
(
�
′
)
,
�
�
=
�
�
�
�
�
(
�
′
)
,
.
.
.
，我们还可以得到小数部分xf=x′−xi,yf=y′−yi,...
�
�
=
�
′
−
�
�
,
�
�
=
�
′
−
�
�
,
.
.
.
，这些小数部分可以帮助我们进一步判断输入点所在的单形以及计算权重。

但我们的目标其实是要得到输入点所在的单形，而不是超立方体。因此我们需要继续做判断。还是如之前的图所示，经过坐标偏斜后，一个正方形由两个三角形组成，我们可以判断xf
�
�
和yf
�
�
之间的关系来判断输入点位于哪个三角形内，并得到该三角形的三个顶点。由此，我们有了Simplex噪声的第二步：

2 单形分割：我们把之前得到的(xf,yf,...)
(
�
�
,
�
�
,
.
.
.
)
中的数值按降序排序，来决定输入点位于变形后的哪个单形内。这个单形的顶点是由按序排列的(0, 0, …, 0)到(1, 1, …, 1)中的n+1
�
+
1
个顶点组成，共有n!
�
!
种可能性。我们可以按下面的过程来得到这n+1
�
+
1
个顶点：从零坐标(0, 0, …, 0)开始，找到当前最大的分量，在该分量位置加1，直至添加了所有分量。例如，对于二维空间来说，如果xf,yf
�
�
,
�
�
满足xf>yf
�
�
>
�
�
，那么对应的3个单形坐标为：首先找到(0, 0)，由于x分量比较大，因此下一个坐标是(1, 0)，接下来是y分量，坐标为(1, 1)；对于三维空间来说，如果xf,yf,zf
�
�
,
�
�
,
�
�
满足xf>zf>yf
�
�
>
�
�
>
�
�
，那么对应的4个单形坐标位：首先从(0, 0, 0)开始，接下来在x分量上加1得(1, 0, 0)，再在z分量上加1得(1, 0, 1)，最后在y分量上加1得(1, 1, 1)。这一步的算法复杂度即为排序复杂度O(n2)
�
(
�
2
)
。

找到了对应的单形后，后面的工作就比较简单了。我们首先找到该单形各个顶点上的伪随机梯度向量，这就是第三步：

3 梯度选取：我们在偏斜后的超立方体网格上获取该单形的各个顶点的伪随机梯度向量。

现在我们需要的东西基本都准备好了，最后一步就是计算所有单形顶点对输出的噪声贡献度。

4 贡献度取和：我们首先需要把单形顶点变回到之前由单形组成的单形网格。这一步需要使用第一步公式的逆函数来求得：
x=x′+(x′+y′+...)⋅K2y=y′+(x′+y′+...)⋅K2...其中，K2=1n+1√−1n
�
=
�
′
+
(
�
′
+
�
′
+
.
.
.
)
⋅
�
2
�
=
�
′
+
(
�
′
+
�
′
+
.
.
.
)
⋅
�
2
.
.
.
其
中
，
�
2
=
1
�
+
1
−
1
�

我们由此可以得到输入点到这些单形顶点的位移向量。这些向量有两个用途，一个是为了和顶点梯度向量点乘，另一个是为了得到之前提到的距离值 dist
�
�
�
�
，来据此求得每个顶点对结果的贡献度：
(r2−|dist|2)4×dot(dist,grad)
(
�
2
−
|
�
�
�
�
|
2
)
4
×
�
�
�
(
�
�
�
�
,
�
�
�
�
)
现在我们可以来解释r2
�
2
取0.5的原因了。由于要求经过第一步坐标偏斜后得到的网格宽度为1，因此我们可以倒推出在变形前单形网格中每个单形边的边长为23−−√
2
3
，这样一来单形每个顶点到对面边的距离（即高）的长度为2√2
2
2
，它的平方即为0.5。很奇妙的是，不仅是二维，在其他维度下，每个单形顶点到对面边/面的距离都是0.5。

至此，我们解释了Simplex噪声的实现。虽然理解上Simplex噪声相比于Perlin噪声更难理解，但由于它的效果更好、速度更优，因此很多情况下会替代Perlin噪声。

效果
下面是Simplex噪声和fbm组合之后的一些效果：

它的主要代码如下：

float simplex_noise(vec2 p)
{
const float K1 = 0.366025404; // (sqrt(3)-1)/2;
const float K2 = 0.211324865; // (3-sqrt(3))/6;

vec2 i = floor(p + (p.x + p.y) * K1);

vec2 a = p - (i - (i.x + i.y) * K2);
vec2 o = (a.x < a.y) ? vec2(0.0, 1.0) : vec2(1.0, 0.0);
vec2 b = a - o + K2;
vec2 c = a - 1.0 + 2.0 * K2;

vec3 h = max(0.5 - vec3(dot(a, a), dot(b, b), dot(c, c)), 0.0);
vec3 n = h * h * h * h * vec3(dot(a, hash22(i)), dot(b, hash22(i + o)), dot(c, hash22(i + 1.0)));

return dot(vec3(70.0, 70.0, 70.0), n);
}

我还是要稍微解释下上面的代码。vec2 i即为我们在第二步中提到的超立方体索引号（也就是超立方体中的(0, 0)点）。vec2 a是在变形前输入点到(0, 0)点的距离向量。接着，我们通过判断a的x分量和y分量的大小（变形前后不会对结果有影响，因此这里直接使用变形前的距离向量），来得到输入点所在的单形顶点。接着，我们计算输入点到第二个单形顶点的距离向量vec2 b以及到第三个单形顶点的距离向量vec2 c。然后，我们计算每个顶点的r2−|dist|2
�
2
−
|
�
�
�
�
|
2
，取r2
�
2
为0.5，并把结果截取到不小于0的部分，得到每个顶点的权重vec3 h。之后，我们计算每个顶点的梯度向量和距离向量的点乘结果，并和它们的权重相乘得到vec3 n。在把它们相加并返回最终结果前，我们需要保证返回值的范围在-1到1，这就需要我们计算n每个分量相加后的最大值。这个最大值可以在输入点在某一边中点时取得，此时|a|=2√2,|b|=|c|=16√
|
�
|
=
2
2
,
|
�
|
=
|
�
|
=
1
6
，得h=(0,13,13)
ℎ
=
(
0
,
1
3
,
1
3
)
。取最大值时，梯度和距离向量的点乘结果可以认为是两者模的乘积，而梯度模的最大值为2–√
2
，因此最后和的最大值为：

134⋅16–√⋅2–√⋅2≈170
1
3
4
⋅
1
6
⋅
2
⋅
2
≈
1
70
因此，我们最后把结果乘以70。那么，如果r2
�
2
取0.6，最后需要乘以多少呢？答案大约为24.51。利用这个想法，我们可以在任意维度下计算最后的伸缩值，例如在三维下，单形，即正四面体的边长为3√2
3
2
，当r2
�
2
取0.5时，最后大概需要乘以31.32。

可平铺的噪声
这部分是新加的。可平铺的噪声就是指那些可以tiling的、seamless的噪声，因为很多时候我们想要让噪声纹理可以无缝连接，例如在生成地形时。按照我们之前提到的方法直接产生噪声，得到的噪声纹理其实是不可以平铺的，你可以看生成纹理的左右、上下其实是不一样的。那么，怎么生成可平铺的噪声纹理呢？

我直接说目前公认比较好的一种方法，就是在2n维上计算n维可平铺噪声。我们以二维噪声为例，如果我们想要得到二维的无缝Perlin噪声，就需要用四维噪声算法来产生。这种方法是思想是，由于我们想要每个维度都是无缝的，也就是当该维度的值从0变成1的过程中，0和1之间比较是平滑过渡的，这让我们想起了“圆”，绕圆一周就是对该维度的采样过程，这样就可以保证无缝了。因此，对于二维噪声中的x轴，我们会在四维空间下的xz平面上的一个圆上进行采样，而二维噪声的y轴，则会在四维空间下的yw平面上的一个圆上进行采样。这个转化过程很简单，我们只需要使用三角函数sin和cos即可把二维采样坐标转化到单位圆上。同样，三维空间的也是类似的，我们会在六维空间下计算。这种方法不仅适用于Perlin噪声，像Worley噪声这种也同样是适合的。

当然上述方法也有自己的缺点，最明显的就是计算量大大增加，一般噪声的复杂度为O(2n)
�
(
2
�
)
（Simplex噪声例外，是O(n2)
�
(
�
2
)
），是指数增加的。但是由于噪声纹理一般只需要前期计算一次即可，因此大部分时候是可以承担的。

代码的话，Unity Wiki里给出了二维可平铺的Simplex噪声的实现，关键代码如下：

//X, Y is [0..1]
public static float SeamlessNoise( float x, float y, float dx, float dy, float xyOffset ) {
float s = x;
float t = y;

float nx = xyOffset + Mathf.Cos(s * 2.0f * Mathf.PI) * dx / (2.0f * Mathf.PI);
float ny = xyOffset + Mathf.Cos(t * 2.0f * Mathf.PI) * dy / (2.0f * Mathf.PI);
float nz = xyOffset + Mathf.Sin(s * 2.0f * Mathf.PI) * dx / (2.0f * Mathf.PI);
float nw = xyOffset + Mathf.Sin(t * 2.0f * Mathf.PI) * dy / (2.0f * Mathf.PI);

return Noise(nx, ny, nz, nw);
}

其中，xyOffset是指在四维空间某个平面上的偏移，即这个单位圆是以xyOffset为圆心的。所有可以用这种方法来产生无缝噪声的实现都和上面的代码是一样的，它们的区别仅仅在于Noise(nx, ny, nz, nw)的实现，如果它是四维Perlin噪声，那就会产生二维可平铺的Perlin噪声，如果是四维的Worley噪声，就会产生二维可平铺的Worley噪声。

如果你有兴趣更深入地理解这种方法，可以阅读下面的一些文章：

这是出处：http://www.gamedev.net/blog/33/entry-2138456-seamless-noise/
一个有图示的文章，帮助理解：http://ronvalstar.nl/creating-tileable-noise-maps
Unity wiki对于二维无缝Simplex噪声的实现：http://wiki.unity3d.com/index.php/Tileable_Noise
GameDev上关于可平铺噪声的讨论：http://gamedev.stackexchange.com/questions/23625/how-do-you-generate-tileable-perlin-noise

扩展阅读
网上有很多优秀的阅读的资料，这里只是我找到的一小部分（wiki我就不说了，一般是必看的）：

Perlin噪声

这篇详细地解释了真正的Perlin噪声以及和fbm的结合：http://flafla2.github.io/2014/08/09/perlinnoise.html
2005年的这篇论文11的开头部分也给出了不错的Perlin噪声的解释：http://webstaff.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf
GPU Gems的文章：http://http.developer.nvidia.com/GPUGems/gpugems_ch05.html
GPU Gems 2的文章：http://http.developer.nvidia.com/GPUGems2/gpugems2_chapter26.html
大牛scrawk的博客在Unity里实现了GPU Gems里面的方法：https://scrawkblog.com/2013/05/18/gpu-gems-to-unity-improved-perlin-noise/
Value噪声

这个课程比较详细地讲了噪声的来源、应用和实现：http://scratchapixel.com/old/lessons/3d-advanced-lessons/noise-part-1/
网络上很多号称是Perlin噪声的文章讲的其实都是Value噪声。比如这篇非常著名又挺有意思的文章：http://freespace.virgin.net/hugo.elias/models/m_perlin.htm
Simplex噪声

这篇文章讲得很细，如果你想再理解下三维的Simplex噪声可以看看：http://catlikecoding.com/unity/tutorials/simplex-noise/
Shadertoy上也有三维Simplex噪声的实现：https://www.shadertoy.com/view/XsX3zB和我的https://www.shadertoy.com/view/4sc3z2。
fbm

其实几乎所有讲噪声的都会讲和fbm的结合。这篇文章单独拿出来讲了：https://code.google.com/p/fractalterraingeneration/wiki/Fractional_Brownian_Motion
hash

在计算随机值和随机梯度时往往都需要使用哈希函数来进行预计算或实时计算，Shadertoy上有个人总结了不同数据类型组合下的哈希函数：https://www.shadertoy.com/view/4djSRW

参考文献
Perlin K. Course in advanced image synthesis[C]//ACM SIGGRAPH Conference. 1984, 18. ↩
Perlin K. An image synthesizer[J]. ACM Siggraph Computer Graphics, 1985, 19(3): 287-296. ↩
Perlin K, Hoffert E M. Hypertexture[C]//ACM SIGGRAPH Computer Graphics. ACM, 1989, 23(3): 253-262. ↩
Perlin K. Making noise[C]//Proc. of the Game Developer Conference. 1999. ↩
Perlin K. Improving noise[C]//ACM Transactions on Graphics (TOG). ACM, 2002, 21(3): 681-682. ↩
Perlin K. Improving noise[C]//ACM Transactions on Graphics (TOG). ACM, 2002, 21(3): 681-682. ↩
Perlin K. Improving noise[C]//ACM Transactions on Graphics (TOG). ACM, 2002, 21(3): 681-682. ↩
Perlin K. Making noise[C]//Proc. of the Game Developer Conference. 1999. ↩
Perlin K. Noise hardware[J]. Real-Time Shading SIGGRAPH Course Notes, 2001. ↩
Gustavson S. Simplex noise demystified[J]. Linköping University, Linköping, Sweden, Research Report, 2005. ↩
Gustavson S. Simplex noise demystified[J]. Linköping University, Linköping, Sweden, Research Report, 2005.

生成网格地图

需要比较简易的版本，可以直接使用这个方案。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class MapManager : MonoBehaviour
{
public GameObject mapPointPrefab;

public GameObject[,] mapPoint;

public GameObject mapPoints;

// Start is called before the first frame update
void Start()
{
CreateMap();
}

public void CreateMap()
{
mapPoint = new GameObject[10, 10];

for (int i = 0; i < 10; i++)
{
for (int j = 0; j < 10; j++)
{
Vector2 point = new Vector2(-4.5f + i, -4.5f + j);
mapPoint[i,j] = Instantiate(mapPointPrefab, point, this.transform.rotation,mapPoints.transform);
}
}
}
}
设计一个地图管理器

public enum GridState //单元格状态
{
ground,
mountain,
}

public struct Map//地图信息结构体
{
public GameObject gridCube;//Map[x,z]代表的GameObject
public Vector3 gridLocation;//位置信息
public GridState gridState;//单元格的状态
public bool canWalk;//是否可以行走
}

public class MapManager : Singleton<MapManager>
{
public Map[,] map; //地图数据
}
随机高度地图生成

public void Init(int xSize//x轴格数, int zSize//y轴格数, float cellSize//单元格大小)
{
map = new Map[xSize, zSize];

[Header("地图块")]
public GameObject Ground;
public GameObject Mountain;

//随机高度
map[x,z].gridHeight = Random.Range(0f, 5f);

for (int x = 0; x < xSize; x++)
{
for (int z = 0; z < zSize; z++)
{
//生成地图二维坐标
map[x, z].gridLocation = new Vector3(cellSize * x, 0, cellSize * z);

//判断高度给单元格赋上状态
if (gridHeight < 3.6f)
{
map[x, z].gridState = GridState.ground;
}
else if (gridHeight >= 3.6f)
{
map[x, z].gridState = GridState.mountain;
}

//根据单元格的状态生成单元格
switch (map[x, z].gridState)
{
case GridState.ground:
map[x, z].gridCube = Instantiate(Ground, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight, 0);
map[x,z].canWalk = true;
break;
case GridState.mountain:
map[x, z].gridCube = Instantiate(Mountain, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight, 0);
map[x,z].canWalk = false;
break;
}
}

柏林噪声在二维平面生成的结果就像上面的图片。

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public enum GridState
{
ground,
mountain,
lake
}

public struct Map
{
public GameObject gridCube;
public Vector3 gridLocation;
public GridState gridState;
public bool canWalk;
}

public class MapManager : Singleton<MapManager>
{
public Map[,] map; //地图数据
public float sightDistance;

[Header("地图块")]
public GameObject Ground;
public GameObject Mountain;
public GameObject Lake;

[Header("柏林噪声参数")]
public float frequency;//柏林噪声频率
public float scale;//柏林噪声振幅

public void Init(int xSize, int zSize, float cellSize)
{
map = new Map[xSize, zSize];

//柏林噪声伪随机误差
float xRandom = Random.Range(0f, 100f);
float zRandom = Random.Range(0f, 100f);

for (int x = 0; x < xSize; x++)
{
for (int z = 0; z < zSize; z++)
{
//生成地图二维坐标
map[x, z].gridLocation = new Vector3(cellSize * x, 0, cellSize * z);

//柏林噪声生成地图高度信息
float xFloat = x;
float zFloat = z;
float xSizeFloat = xSize;
float zSizeFloat = zSize;
float gridHeight = Mathf.PerlinNoise(xFloat / xSizeFloat * frequency + xRandom, zFloat / zSizeFloat * frequency + zRandom) * scale;

//地图单位格高度判断并更改类型
//生成高山平原湖泊
if (gridHeight > 1.5f && gridHeight < 3.6f)
{
map[x, z].gridState = GridState.ground;
}
else if (gridHeight >= 3.6f)
{
map[x, z].gridState = GridState.mountain;
}
else if (gridHeight <= 1.5f)
{
map[x, z].gridState = GridState.lake;
}

//地图单位格高度设置以及生成
switch (map[x, z].gridState)
{
case GridState.ground:
map[x, z].gridCube = Instantiate(Ground, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight, 0);
map[x,z].canWalk = true;
break;
case GridState.mountain:
map[x, z].gridCube = Instantiate(Mountain, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight + 1f, 0);
map[x,z].canWalk = false;
break;
case GridState.lake:
map[x, z].gridCube = Instantiate(Lake, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, 1.4f, 0);
map[x,z].canWalk = false;
break;
}
}
}
}
}

在代码中，我新建了一个Lake的状态，在高度为1.5以下时表现为湖泊。

最重要的代码是这段

float xRandom = Random.Range(0f, 100f);
float zRandom = Random.Range(0f, 100f);
------------------------------------------
float xFloat = x;
float zFloat = z;
float xSizeFloat = xSize;
float zSizeFloat = zSize;

float gridHeight = Mathf.PerlinNoise(xFloat / xSizeFloat * frequency + xRandom, zFloat / zSizeFloat * frequency + zRandom) * scale;

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public enum GridState
{
ground,
mountain,
lake,
forest,
desert
}

public struct Map
{
public GameObject gridCube;
public Vector3 gridLocation;
public GridState gridState;
public bool canWalk;
}

public class MapManager : Singleton<MapManager>
{
public Map[,] map; //地图数据
public float sightDistance;

[Header("地图块")]
public GameObject Ground;
public GameObject Mountain;
public GameObject Lake;
public GameObject Forest;
public GameObject Desert;

[Header("柏林噪声参数")]
public float frequency;//柏林噪声频率
public float scale;//柏林噪声振幅

public void Init(int xSize, int zSize, float cellSize)
{
map = new Map[xSize, zSize];

//柏林噪声伪随机误差
float xRandom = Random.Range(0f, 100f);
float zRandom = Random.Range(0f, 100f);

for (int x = 0; x < xSize; x++)
{
for (int z = 0; z < zSize; z++)
{
//生成地图二维坐标
map[x, z].gridLocation = new Vector3(cellSize * x, 0, cellSize * z);

//柏林噪声生成地图高度信息
float xFloat = x;
float zFloat = z;
float xSizeFloat = xSize;
float zSizeFloat = zSize;
float gridHeight = Mathf.PerlinNoise(xFloat / xSizeFloat * frequency + xRandom, zFloat / zSizeFloat * frequency + zRandom) * scale;
float gridType = Mathf.PerlinNoise(xFloat / xSizeFloat * frequency + xRandom/3, zFloat / zSizeFloat * frequency + zRandom/3) * scale;

//地图单位格高度判断并更改类型
//生成高山平原湖泊
if (gridHeight > 1.5f && gridHeight < 3.6f)
{
map[x, z].gridState = GridState.ground;
}
else if (gridHeight >= 3.6f)
{
map[x, z].gridState = GridState.mountain;
}
else if (gridHeight <= 1.5f)
{
map[x, z].gridState = GridState.lake;
}

//生成森林沙漠
if (map[x, z].gridState == GridState.ground)
{
if (gridType >= 3.2f)
{
map[x, z].gridState = GridState.forest;
}
else if (gridType <= 1.5f)
{
map[x, z].gridState = GridState.desert;
}
}

//地图单位格高度设置以及生成
switch (map[x, z].gridState)
{
case GridState.ground:
map[x, z].gridCube = Instantiate(Ground, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight, 0);
map[x,z].canWalk = true;
break;
case GridState.mountain:
map[x, z].gridCube = Instantiate(Mountain, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight + 1f, 0);
map[x,z].canWalk = false;
break;
case GridState.lake:
map[x, z].gridCube = Instantiate(Lake, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, 1.4f, 0);
map[x,z].canWalk = false;
break;
case GridState.forest:
map[x, z].gridCube = Instantiate(Forest, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight, 0);
map[x,z].canWalk = true;
break;
case GridState.desert:
map[x, z].gridCube = Instantiate(Desert, map[x, z].gridLocation, Quaternion.identity, this.transform);
map[x, z].gridCube.transform.position = map[x, z].gridLocation + new Vector3(0, gridHeight, 0);
map[x,z].canWalk = true;
break;
}
}
}
}
｝