一、求Fibonacci数列前40个数。这个数列有以下特点：第1，2两个数为1，1。从第3个数开始，该数是其前面两个数之和。即

F1=1                 (n=1)

F2=2                 (n=2)

Fn=Fn-1+Fn-2(n>=3)

    这是一个有趣的古典数学问题：有一对兔子，从出生后第3个月起每个月都生一对兔子。小兔子长到第3个月后每个月又生一对兔子。假设所有兔子都不死，问每个月的兔子总数为多少？

    不满1个月的为小兔子，满1个月不满2个月的为中兔子，满3个月以上的为老兔子。可以看到每个月的兔子总数依次为1，1，2，3，5，8，13，...。这就是Fibonacci数列。

    根据给出的每月兔子总数的关系，可编写程序如下：

#include<iostream>
#include<iomanip>
using namespace std;
int main()
{
    long f1,f2;
    int i;
    f1=f2=1;
    for(i=1;i<=20;i++)
    {
    cout<<setw(12)<<f1<<setw(12)<<f2;//设备输出字段宽度为12，每次输出两个数
    if(i%2==0) cout<<endl;           //每输出完4个数后换行，使每行输出4个数
    f1=f1+f2;                        //左边的f1代表第3个数，是第1，2两个数之和
    f2=f2+f1;                        //左边的f2代表第4个数，是第2，3两个数之和
    }
    return 0;
}

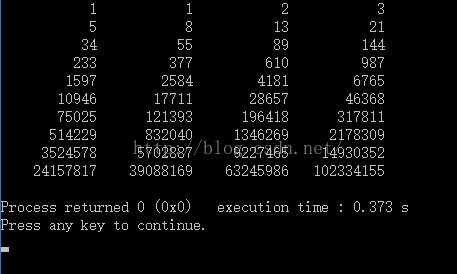
运行结果如下：

二、用递归法计算斐波那契数列的第n项

斐波纳契数列（Fibonacci Sequence）又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……在数学上，斐波纳契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=F(n-1)+F(n-2)（n>=2，n∈N*）在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1960年代起出版了《斐波纳契数列》季刊，专门刊载这方面的研究成果。

#include <stdio.h>  
int Fibonacci(int n)  
{  
 if( n == 1 || n == 2) // 递归结束的条件，求前两项  
  return 1;  
 else  
  return Fibonacci(n-1)+Fibonacci(n-2); // 如果是求其它项，先要求出它前面两项，然后做和。  
}  
  
int main()  
{  
 int n;  
 printf("please input n: ");  
 scanf("%d",&n);  
 printf("Result: %d\n",Fibonacci(n));  
 return 0;  
}