KMP算法

时间复杂度O(n + m)

NFA：不确定性有穷状态自动机

int *getNext(const char *t, int *len){
    *len = strlen(t);
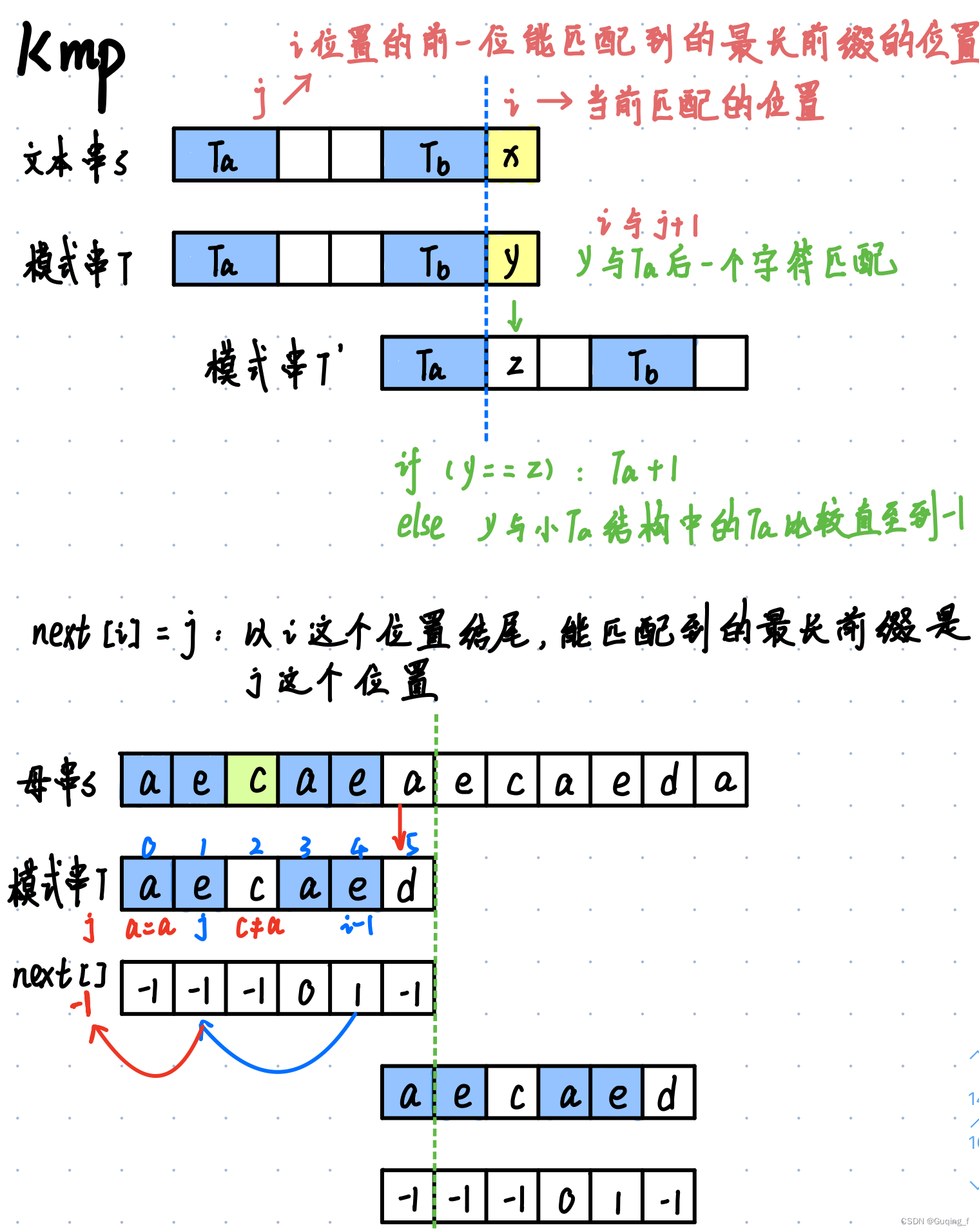
    int *next = (int *) malloc (sizeof(int) * (*len)); // next[i] = j : 以i位置结尾，所匹配到的最长前缀是j这个 位置
    next[0] = -1; //匹配最长前缀不能包含自己，第一位的最长前缀为-1
    for(int i = 1, j = -1; t[i]; i++){
        //i是当前匹配的位置，j是i的前一位能匹配到的最长前缀的位置。所以i与j+1比较
        while(j != -1 && t[j + 1] != t[i]) j = next[j]; //匹配不成功就往前找
        if(t[j + 1] == t[i]) ++j; //匹配成功就按照i-1位置最长前缀的数量+1
        next[i] = j;//更新next数组
    }

    return next;
}

int kmp(const char *s, const char *t){
    int len = 0;
    int *next = getNext(t, &len); //初始化next数组
    //j代表之前成功匹配过的模式串在第几位
    for(int i = 0, j = -1; s[i]; i++){ 
        while(j != -1 && t[j + 1] != s[i]) j = next[j]; //NFA(不确定性)
        if(t[j + 1] == s[i]) ++j;
        if(t[j + 1] == '\0') { //完全成功匹配了模式串
            free(next);
            return i - len + 1;
        }
    }
    free(next);
    return -1;
}

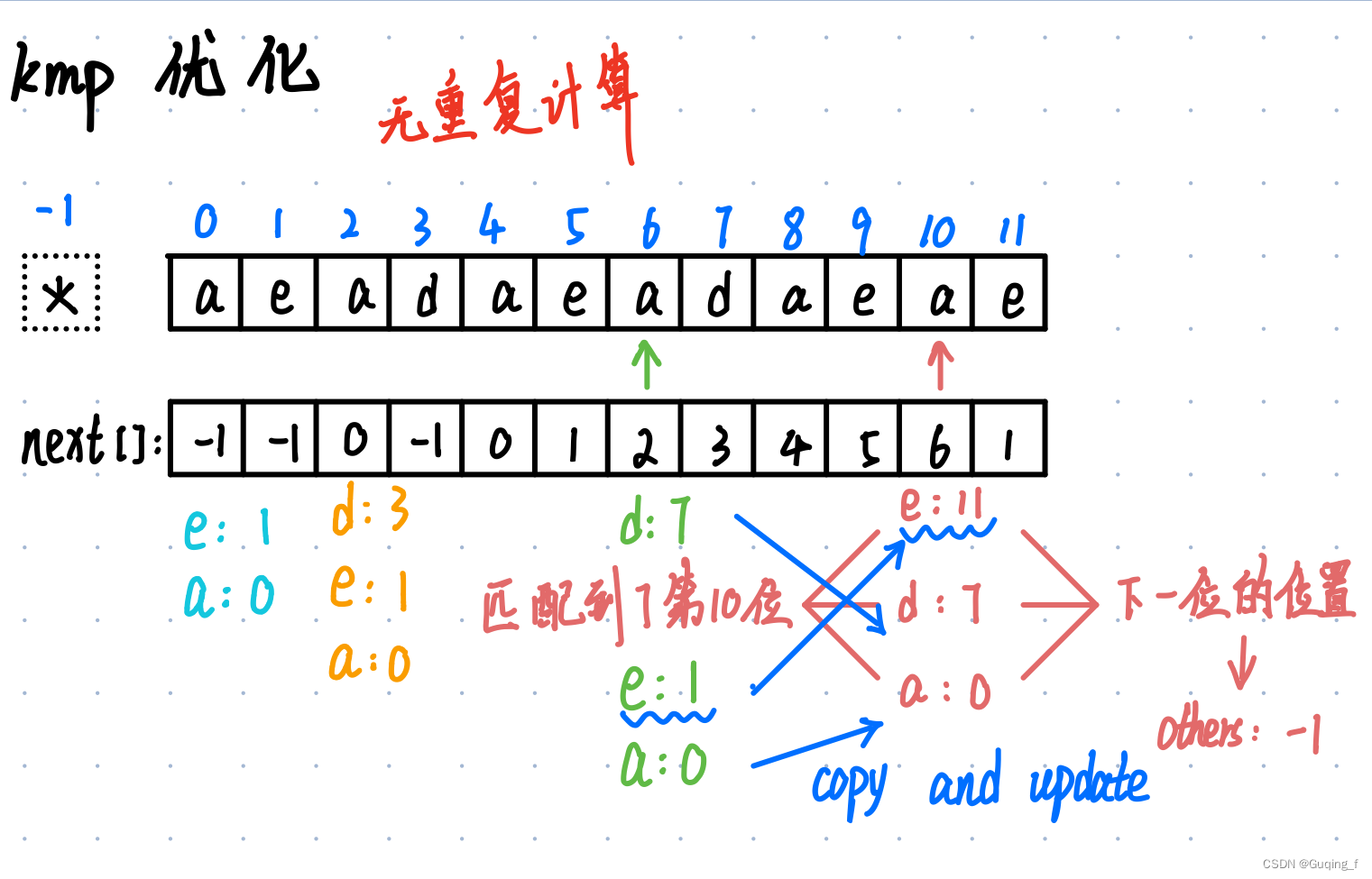
KMP的优化：

DFA：确定性有穷状态自动机

void free_next(int *next){
    free(next);
    return ;
}

void free_jump(int **jump, int len){
    for(int i = 0; i < len; i++) free(jump[i - 1]);
    free(jump - 1);
    return ;
}

//获取跳转信息的数组
int **getJump(int *next, const char *t, int n){
    int **jump = (int **) malloc(sizeof(int *) * n);
    for(int i = 0; i < n; i++) jump[i] = (int *) malloc(sizeof(int) * 26);
    ++jump; //让jump指向next数组1的位置，使它访问-1位置的时候实际上访问的是0，合法的
    for(int i = 0; i < 26; i++) jump[-1][i] = -1;
    jump[-1][t[0] - 'a'] = 0; //模式串的第一个字符
    for(int i = 0, I = n - 1; i < I; i++){
        for(int j = 0; j < 26; j++) jump[i][j] = jump[next[i]][j];
        jump[i][t[i + 1] - 'a'] = i + 1;
    }
    return jump;
}

//Kmp的优化算法
int kmp_opt(const char *s, const char *t){
    int len = 0;
    int *next = getNext(t, &len);
    int **jump = getJump(next, t, len); 
    //j代表之前成功匹配过的模式串在第几位
    for(int i = 0, j = -1; s[i]; i++){ 
        j = jump[j][s[i] - 'a']; //DFA(确定性)
        if(j == len - 1){ //已找到字符串
            free_next(next);
            free_jump(jump, len);
            return i - len + 1;
        }
    }
    free_next(next);
    free_jump(jump, len);
    return -1;
}

字符串匹配算法合集：
六种字符串匹配算法详解