折半插入排序(Binary Insertion Sort)是对插入排序算法的一种改进。所谓插入排序,就是不断的依次将元素插入前面已排好序的序列中。由于前半部分为已排好序的数列,这样我们不用按顺序依次寻找插入点,可以采用折半查找的方法来加快寻找插入点的速度。
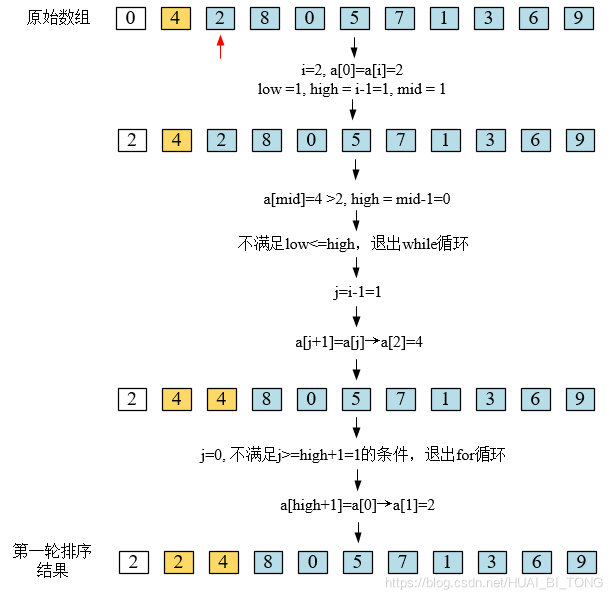
具体操作: 在将一个新元素插入已排好序的数组的过程中,寻找插入点时,将待插入区域的首元素设置为a[low],末元素设置为a[high]。将待插入元素与a[mid](其中mid=low+(high-low)/2)相比较,如果比参考元素小,则选择a[low]到a[mid-1]为新的插入区域(即high=mid-1),否则选择a[mid+1]到a[high]为新的插入区域(即low=mid+1),如此直至low<=high不成立,即将high+1位置及之后所有元素后移一位,并将新元素插入a[high+1]。
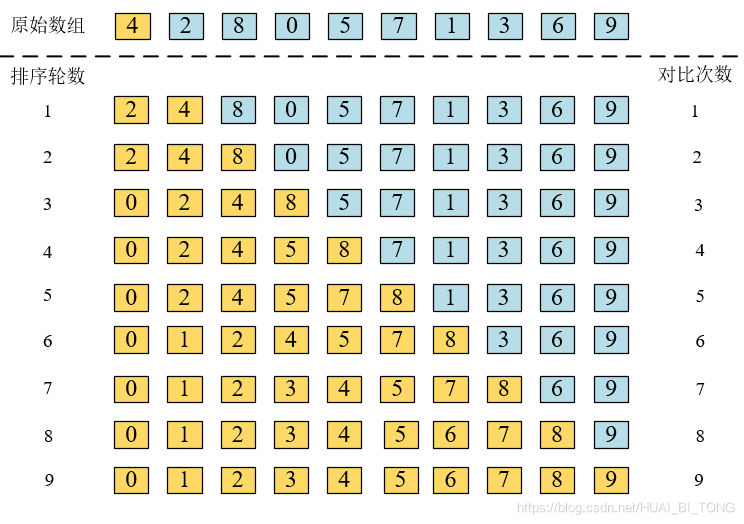
例如: 使用折半插入排序算法将数组 { 4,2,8,0,5,7,1,3,6,9 } 进行升序排序。
实现代码如下所示。
#include<iostream>
using namespace std;
template<class T>
void BinaryInsertionSort(T *a, int n)
{
int i, j, low, high, mid;
for (i = 2; i < n; i++) //依次将a[2]~a[n]插入到前面已经排好序的列表
{
a[0] = a[i]; //将a[i]暂存到a[0]
low = 1;
high = i - 1;
while (low <= high)
{
mid = low + (high - low) / 2; //取中间位置(利用low + (high - low) / 2求mid是为了防止整数溢出问题)
if (a[mid] > a[0]) //查找左子表
{
high = mid - 1;
}
else //查找右子表
{
low = mid + 1;
}
}
for (j = i - 1; j >= high + 1; --j) //i - 1指待插入元素的前一个元素,即有序列表中所有大于待插入元素的最后一个元素;high + 1指有序列表中所有大于待插入元素的第一个元素
{
a[j + 1] = a[j]; //统一后移元素
}
a[high + 1] = a[0]; //插入操作
}
}
int main()
{
int a[] = { 0,4,2,8,0,5,7,1,3,6,9 };
cout << "排序前:" << endl;
for (int i = 1; i < 11; i++)
{
cout << a[i] << " ";
}
cout << endl;
BinaryInsertionSort(a, 11);
cout << "排序后:" << endl;
for (int i = 1; i < 11; i++)
{
cout << a[i] << " ";
}
cout << endl;
double b[] = { 0,4.1,2.2,8.3,0.4,5.5,7.6,1.7,3.8,6.9,9.0 };
cout << "排序前:" << endl;
for (int i = 1; i < 11; i++)
{
cout << b[i] << " ";
}
cout << endl;
BinaryInsertionSort(b, 11);
cout << "排序后:" << endl;
for (int i = 1; i < 11; i++)
{
cout << b[i] << " ";
}
cout << endl;
system("pause");
return 0;
}
排序前:
4 2 8 0 5 7 1 3 6 9
排序后:
0 1 2 3 4 5 6 7 8 9
排序前:
4.1 2.2 8.3 0.4 5.5 7.6 1.7 3.8 6.9 9
排序后:
0.4 1.7 2.2 3.8 4.1 5.5 6.9 7.6 8.3 9
需要注意的是,在上述代码中,为防止整数溢出问题的出现,在求中间的下标mid时,使用mid = low + (high - low) / 2;,而不是mid = (high + low) / 2,详细原因见→为防止整数溢出问题,使用low + (high - low) / 2而不是(high + low) / 2。
原始数组的第一轮排序代码运行的中间过程如下图所示。
时间复杂度: 折半插入排序算法比直接插入排序算法明显减少了关键字之间比较的次数,因此速度比直接插入排序算法快,但记录移动的次数没有变,所以折半插入排序算法的时间复杂度仍然为
O
(
n
2
)
O(n^2)
O(n2),与直接插入排序算法相同。
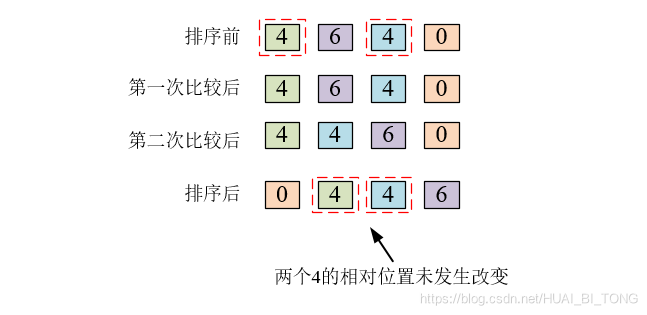
稳定性: 由于在比较的时候,对于两个相等的元素,不会进行移动,排序完成后,相同元素之间的先后顺序不变,所以折半插入排序算法是一种稳定的排序算法,如下图所示。