信息熵

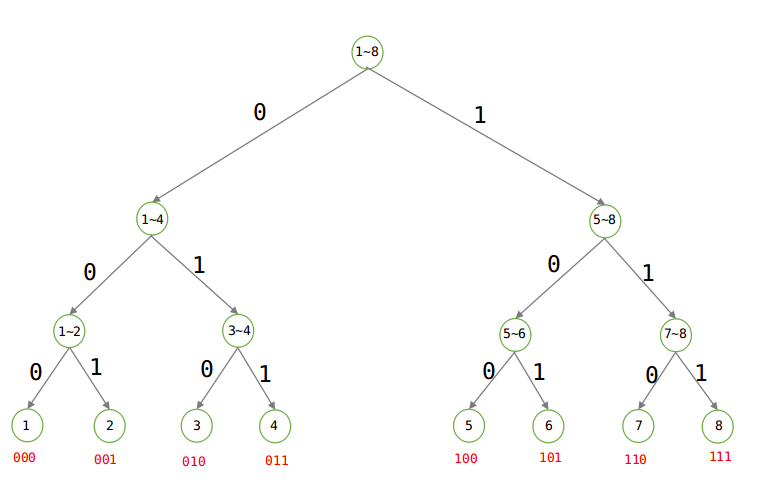
首先我们来介绍一下信息熵。信息熵又叫KL散度，是信息的平均编码长度。给定信息出现的概率向量$p=(p_1,p_2,...,p_n)$，其中$p_i$为第$i$条信息出现的概率，那么信息的平均编码长度为$H(p)={\sum }_i^n{p}_i\log \frac{1}{p_i}$。举一个例子，比如现在要用为8个字符进行编码，每个字符出现的概率为$1/8$，用Huffman树可求出最短编码方案，此时的Huffman树为：

可以计算出各点的深度为$\log \frac{1}{p_i}$，再乘上期望求和便是信息熵。当然，公式中$\log \frac{1}{p_i}$指的是只看概率$p_i$而不了解其他信息概率时，该信息编码在对应的Huffman树中最大可能达到深度，因为有可能只有两个信息，一个信息出现概率为7/8，另外一个为1/8，这时候的深度就是1。但是无论概率分布是怎么样的，深度不可能超过$\log \frac{1}{p_i}$。

交叉熵

交叉熵是针对两个概率向量$p$和$q$而言的，公式为$H(p,q)={\sum }_{i=1}^n{p}_i\log \frac{1}{q_i}$。他指的是在信息出现的概率分布为$p$的情况下，不用$p$导出的Huffman树进行编码，而是用另外的一个概率分布$q$导出的Huffman树进行编码的编码长度，而这种编码方案并不是最优的编码方案，$H(p,q)\le H(p)$。

softmax损失函数

接下来我们看如何用交叉熵构建损失函数。比如在多类型分类问题中，对每个类别我们会得到一个评分（可正可负），要使用交叉熵构建损失函数首先要将这些得分转化成概率分布（都是正值）。最著名的方法就是使用softmax。通过softmax可以得到一个概率分布，且是非线性的，更重要的是容易求导。假设得分向量为$z$，转化后的概率向量为$y$，那么sofrtmax做的就是令$y_i=e^{z_i}/{\sum }_{j=1}^n{e}^{z_j}$。之后交叉熵损失函数为$L=\sum \widehat{y_i}\log \frac{1}{y_i}$，这里$y_i$是网络估计为第i类的概率，而$\widehat{y_i}$是真实的概率分布，一般状况下训练样本属于哪一类是确定的，$\hat{y}$向量里只有一项是1其他都是0，因此损失函数$L$最终只会保留求和里面的一项，即$L=\log \frac{1}{y_{\hat{i}}}$,其中$\hat{i}$是样本属于的类别。这样的交叉熵损失函数就叫做softmax损失函数。在模型训练过程中就是通过对损失函数求导，用梯度下降降低损失函数，这意味着分布$y$越接近$\hat{y}$。