前言

优化问题（即高数中的求极值）可分为三类：无约束、等式约束、不等式约束。

我们可以通过拉格朗日乘数法对其求解，但是拉格朗日也有一些问题，这些问题与使用求导法找最值的问题是相同的：就是使用这种方法找出来的点，不一定是最值对应的点，也有可能是极值，也有可能是鞍点。

但是如果我们的目标函数是一个凸问题，由于凸问题不存在鞍点，并且凸问题的极值点一定是最值点。但是凸问题是一个可遇不可求的事情，那么对于非凸问题我们可以去看它的拉格朗日对偶问题，在满足一定条件下，拉格朗日对偶问题一定是凸问题。

凸优化问题：目标函数是凸函数，并且约束条件是凸集

所以我们可以使用拉格朗日函数乘子法来求解凸问题，此时求得的极值点一定是最值点

一、无约束优化

当我们希望找到一个或多个变量或参数 $\vec{x}$ 的取值，使得目标函数 $f(\vec{x})$ 的值尽可能小时，我们称为最小化问题。

$$\begin{array}{r}\underset{\text{x}}{\mathrm{minimize}}f(\vec{x})\end{array}$$一个函数的极值点可以通过求驻点得到，也就是一维下导数为0的点，高维下梯度为0的点。至于这些驻点有没有取到极值？是极大值还是极小值？需要额外的信息，比如二阶导来判断。所以导数为0的点是极值点点必要条件，而不充分。这种求最值的问题被称为无约束优化，因为我们没有对自变量的取值范围进行限制，自变量的范围就是定义域。

最大化的问题可以通过取相反数变成一个最小化的问题，所以我们可以只研究最小化问题，而不失一般性

无约束优化可以看作是解决最小化问题的一种具体优化方法。求解无约束优化问题的方法有多种，以下是一些常见的求解方法：

• 梯度下降法（Gradient Descent）：梯度下降法是一种基本的优化算法，通过迭代地更新参数来最小化目标函数。在每次迭代中，根据目标函数关于参数的梯度方向和大小，更新参数值。梯度下降法直至达到停止准则或收敛条件时停止迭代。
• 牛顿法（Newton’s Method）：牛顿法是一种迭代的优化算法，在每次迭代中，根据目标函数的梯度和海森矩阵来更新参数。牛顿法通常比梯度下降法更快地收敛到最优解，但也需要计算和存储海森矩阵的逆，可能对计算资源要求较高。
• 拟牛顿法（Quasi-Newton Methods）：拟牛顿法是对牛顿法的改进，通过近似估计海森矩阵的逆而不需要显式计算。使用历史参数和梯度信息来构造一个对海森矩阵逆的估计，然后用此估计来更新参数。著名的拟牛顿法包括L-BFGS（Limited-memory Broyden–Fletcher–Goldfarb–Shanno）算法。
• 共轭梯度法（Conjugate Gradient）：共轭梯度法是用于求解二次函数形式的优化问题的一种迭代方法。它利用了共轭向量的性质，通过迭代地寻找使目标函数沿着不同方向共轭的最优解。

可参考：https://link.zhihu.com/?target=http%3A//www.cnblogs.com/zhangchaoyang/articles/2600491.html

二、等式约束优化

当我们希望找到一个或多个变量或参数 $\vec{x}$ 的取值，使得目标函数 $f(\vec{x})$ 在满足等式约束 $g(\vec{x})$ 的条件下的值尽可能小时，我们称为等式约束的最小化问题。
$$\begin{array}{r}\underset{\text{x}}{\mathrm{minimize}}f(\vec{x})\\ st.g(\vec{x})=0\end{array}$$可以使用拉格朗日乘子法来求解该等式约束优化问题，以下是详细说明：

1. 拉格朗日乘子法步骤

拉格朗日乘子法（Lagrange Multiplier Method）：拉格朗日乘子法将约束优化问题转化为一个无约束优化问题。通过构建拉格朗日函数，该函数包含原目标函数和约束函数，并引入拉格朗日乘子来实现约束条件的考虑。然后，通过最小化或最大化这个拉格朗日函数，可以求解出满足约束条件的最优解。

以下是使用拉格朗日乘子法来求解等式约束最小化问题的步骤：

1.构建拉格朗日函数（Lagrange function）将等式约束引入目标函数，构建拉格朗日函数：设目标函数为$f(x)$，等式约束为$g(x)=0$，且$\nabla g(\overrightarrow{x^{\ast }})!=0$【多约束条件下所有的 $\nabla g_i(x)$ 线性无关】。拉格朗日函数为：
$$\begin{array}{r}L(x,\lambda )=f(x)+\lambda g(x)\\ g(x)=0\end{array}$$2.接下来我们只需要使拉格朗日函数最小化，这样就变成了无约束问题，接下来可以求取拉格朗日函数对$x$和$\lambda$的偏导数解方程来得到最小值，也可以使用我们上述提到的无约束求解法来求解：

$$\begin{array}{r}\frac{\partial L}{\partial x}=\nabla f(x)+\lambda \nabla g(x)=0\\ g(x)=0\end{array}$$3.解方程组： 根据第2步得到的方程组，可以联立求解 $\nabla f(x)+\lambda \nabla g(x)=0$ 和 $g(x)=0$。,这样可以求得一组满足等式约束的最优解 $x^{\ast }$ 和相应的拉格朗日乘子 ${\lambda }^{\ast }$。

需要注意的是，拉格朗日乘子法求解等式约束的最小化问题，要求目标函数 $f(x)$ 可微分及等式约束函数 $g(x)$ 满足某些光滑性条件。在实践中，可以使用数值优化方法如牛顿法、拟牛顿法等来求解方程组，从而得到最优解。

2. 拉格朗日乘子法理解

例如如何我们想要求 $f(x_1,x_2)=x_1+x_2$ 这个函数在约束 $x_1^2+x_2^2=1,即h(x_1,x_2)=x_1^2+x_2^2-1$ 的条件下求最小值：

我们在平面上把函数取值相同的点连接起来，就变成了等高线：

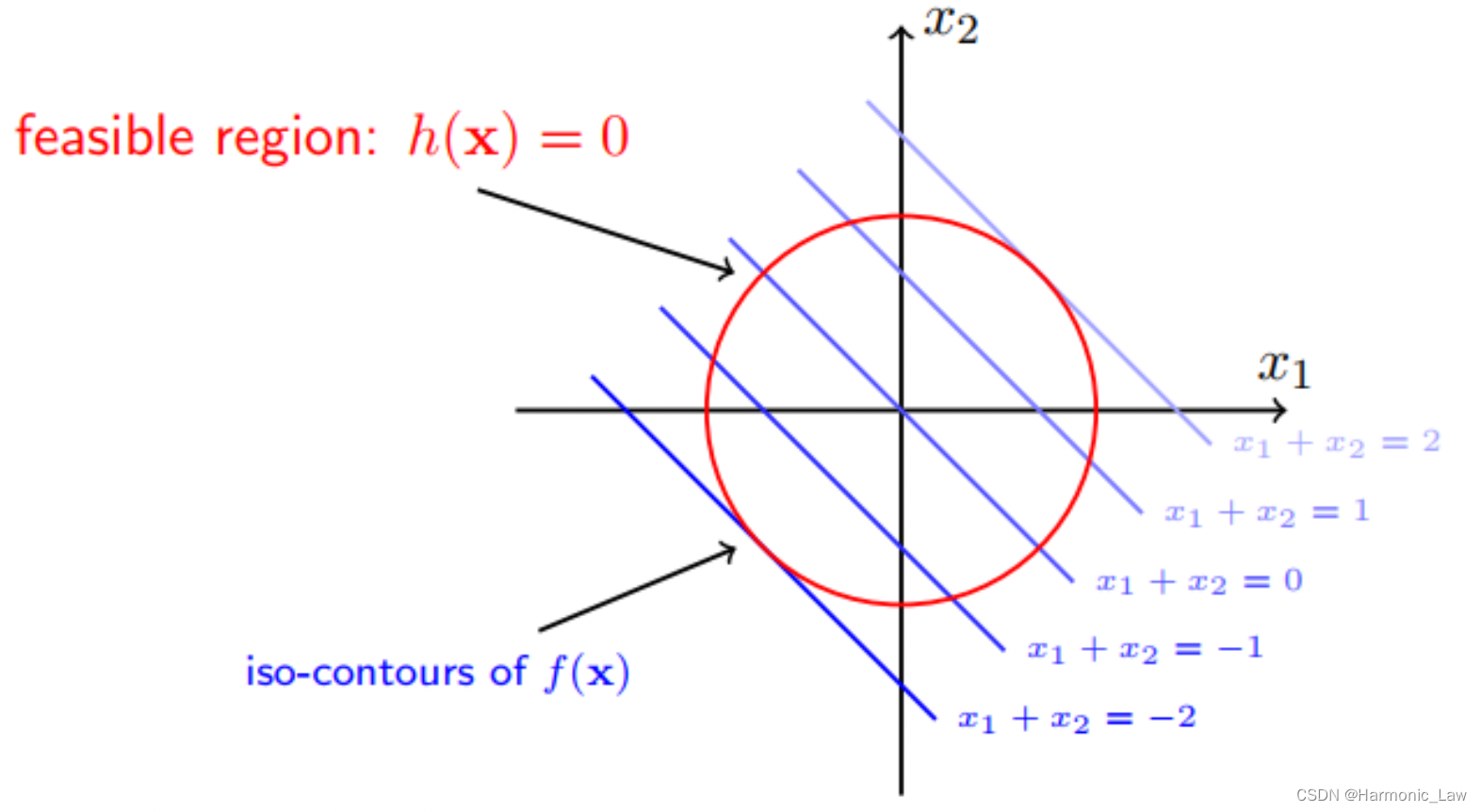
接下来画出二者的梯度方向【蓝线相反的方向是$f(x_1,x_2)$的梯度方向】：

我们知道梯度是函数值增大最快的方向，那么当 点$(x_1,x_2)$ 沿着梯度的锐角方向进行移动，那么对应函数的值就会变大；当 点$(x_1,x_2)$ 沿着梯度的钝角的方向进行移动，那么对应函数的值就会变小；沿着梯度垂直的方向移动，函数值不变。

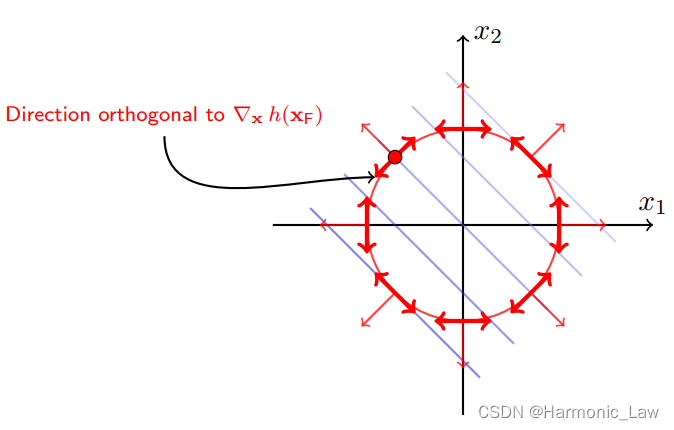
那么要如何判断在圆(约束条件)上的 点$(x_1,x_2)$ 对应的 $f(x_1,x_2)$ 的值最小呢？那么就需要看 点$(x_1,x_2)$ 能否保持在圆上的情况下，使 $f(x_1,x_2)$ 的函数值减小。用梯度来刻画就是 方向 $\vec{v}$ 既和约束条件梯度垂直，又和目标函数的梯度成钝角。那么极值点就应该是可行方向 $\vec{v}$ 既和约束条件梯度垂直，又和目标函数的梯度 即不成钝角，也不是锐角，而是直角，也就是与目标函数的梯度垂直。

既然方向 $\vec{v}$ 既和约束条件梯度垂直，又和目标函数梯度垂直，那么约束条件的梯度方向和目标函数的梯度方向应该平行。

$$\begin{array}{r}\nabla f(x)+\lambda \nabla g(x)=0\end{array}$$

• 如果梯度方向和目标函数的梯度方向同向，那么该点就对应了目标函数的最大值，此时 $\lambda <0$
• 如果梯度方向和目标函数的梯度方向反向，那么该点就对应了目标函数的最小值，此时 $\lambda >0$

而对于多个不等式约束，拉格朗日乘子法仍然适用：约束条件的可行方向 $\vec{v}$ 既和所有约束条件的梯度垂直，也就是垂直于可行方向张成的空间，又和目标函数梯度垂直。 也就是目标函数的梯度位于约束条件梯度张成的空间中
$$\begin{array}{r}\nabla f(x)+\sum _i^n{\lambda }_i\nabla g_i(x)=0\\ g_i(x)=0(i=0,1,\mathrm{2....}n)\end{array}$$

三、不等式约束优化

1. 使用KKT条件解不等式约束优化

当我们希望找到一个或多个变量或参数 $\vec{x}$ 的取值，使得目标函数 $f(\vec{x})$ 在满足不等式约束 $g_i(\vec{x})<=0$ 的条件下的值尽可能小时，我们称为不等式约束的最小化问题。
$$\begin{array}{r}\underset{\text{x}}{\mathrm{minimize}}f(\vec{x})\\ st.g_i(\vec{x})<=0\\ (i=0,1,\mathrm{2...}n)\end{array}$$可以使用拉格朗日乘子法结合KKT条件来求解该等式约束优化问题，以下是详细说明：

1.构建拉格朗日函数（Lagrange function）：将不等式约束引入目标函数，构建拉格朗日函数。 设目标函数为$f(x)$，不等式约束为$g(x)\le 0$。拉格朗日函数为：
$$\begin{array}{r}L(x,\lambda )=f(x)+\sum _i^n{\lambda }_i{g}_i(x)\end{array}$$2.是否满足KKT条件：
$$\begin{array}{r}{\nabla }_{x}L(x^{\ast },{\lambda }^{\ast })=0\\ {\lambda }_i{g}_i(x^{\ast })=0\\ g_i(x^{\ast })\le 0\\ {\lambda }_i\ge 0\end{array}$$KKT条件是在最优解处的必要条件，当拉格朗日函数满足KKT条件时，最小化拉格朗日函数可以得到最优解

3.接下来我们只需要使拉格朗日函数最小化，这样就变成了无约束问题，接下来可以求取拉格朗日函数对$x$和$\lambda$的偏导数解方程来得到最小值，也可以使用我们上述提到的无约束求解法来求解：

2. KKT条件的理解

（1）最小值在可行域内

考虑目标函数 $f(x_1,x_2)=x_1^2+x_2^2$ 在不等式约束 $g(x_1,x_2)=x_1^2+x_2^2-1<=0$ 下的极小值。

• f(x)的极小值为原点$(0,0)$，落在可行域内。 可行域以原点为圆心，半径为1。
• 这种情况约束不起作用，考虑极小值点$x^{\ast }$， 这个时候，$g(x^{\ast })<0$，$f(x^{\ast })$的梯度等于0。 极小值点落在可行域内（不包含边界）

此时，由于约束条件没$g_i(x)<0$有其作用，也就是${\lambda }_i=0$，那么我们就称约束条件$g_i(x)$是松弛的

那么在 $g(x^{\ast })<0$ 的情况下，求解${\nabla }_{x}f(x^{\ast })=0$，也就是$\lambda =0$时，${\nabla }_{x}L(x^{\ast },{\lambda }^{\ast })=0$，得到的参数 $x^{\ast }$ 便是所求参数

（2）最小值在可行域外

考虑目标函数 不等式约束 $f(x_1,x_2)=(x_1-1{)}^2+(x_2+1{)}^2$，在不等式约束 $g(x_1,x_2)=x_1^2+x_2^2-1<=0$ 下的极小值。

• 显然 $f(x)$ 的极小值为原点$(1,-1)$，落在可行域外。可行域以原点为圆心，半径为$1$。
• 这种情况约束起作用，要考虑求解$f(x)$在可行域内的极小值点。
• 显然，走到极小值点的时候，$g(x)$的梯度 和f(x)的负梯度同向。因为极小值点在边界上 ，这个时候$g(x)$等于$0$。 极小值点落在边界上，此时$g(x)=0$。极小值点落在可行域外（不包含边界）

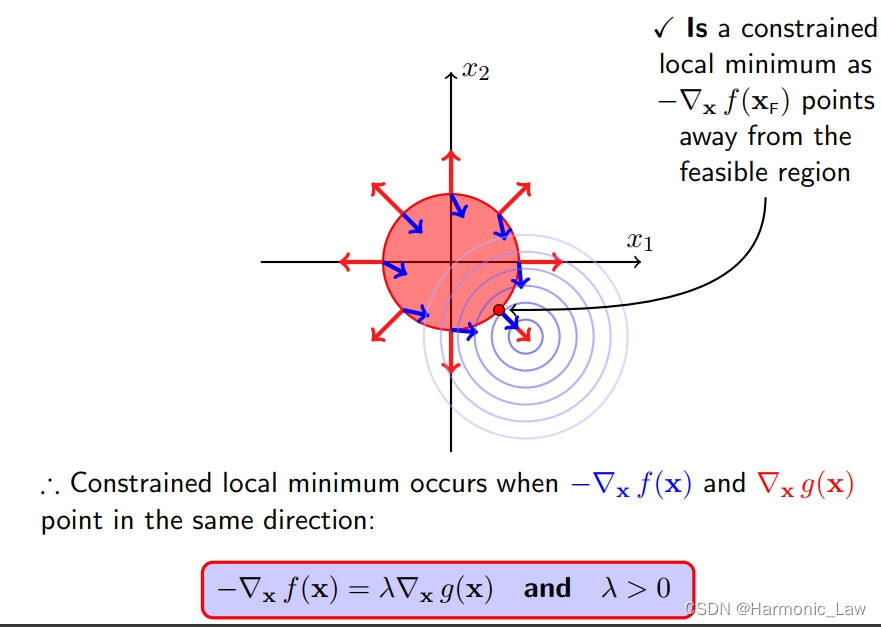
此时，由于约束条没$g_i(x)<0$起到了作用，也就是${\lambda }_i<0$，那么我们就称约束条件$g_i(x)$是紧致的

那么在 $g(x^{\ast })=0$ 的情况下，求解${\nabla }_{x}f(x^{\ast })+\lambda {\nabla }_{x}g(x^{\ast })=0$，并且由于是最小值，二者梯度方向相反，此时的$\lambda >0$，得到的参数 $x^{\ast }$ 便是所求参数

（3）总结

第一种情况：最小值在可行区域内时
$$\begin{array}{r}g(x^{\ast })<0\\ {\nabla }_{x}L(x^{\ast },{\lambda }^{\ast })=0\\ \lambda =0\end{array}$$

第二种情况：最小值在可行域外时
$$\begin{array}{r}g(x^{\ast })=0\\ {\nabla }_{x}L(x^{\ast },{\lambda }^{\ast })=0\\ \lambda >0\end{array}$$

将俩种情况结合起来，我们就得到了KKT条件：

在结合的时候需要注意，$g(x^{\ast })$的取值范围为$g(x^{\ast })<=0$，$\lambda$的取值范围为$\lambda >=0$，但是 $g(x^{\ast })<0，\lambda >0$ 和 $g(x^{\ast })=0，\lambda =0$ 的情况是不能出现的，所以对于二者取值范围还需要进一步限制，这个限制就是 约束条件和拉格朗日乘子互补松弛

使用公式表示为 $\lambda g(x^{\ast })=0$，互补松弛表示约束条件与拉格朗日乘子总有一个是松弛的，该条件限制了$g(x^{\ast })<0，\lambda >0$情况的出现，但是$g(x^{\ast })=0，\lambda =0$的情况要如何处理呢？

当 $g(x^{\ast })=0，\lambda =0$ 时，此时$g(x^{\ast })=0$表示最小值点在可行域外，而$\lambda =0$表示约束条件不起作用，最小值在可行域内部。也就是说明，函数$f(x^{\ast })$的最小值恰好即在可行域边界处，也是此时无论是使用哪一种情况的解决方法都可以解出最小值点对应的参数 $x^{\ast }$。

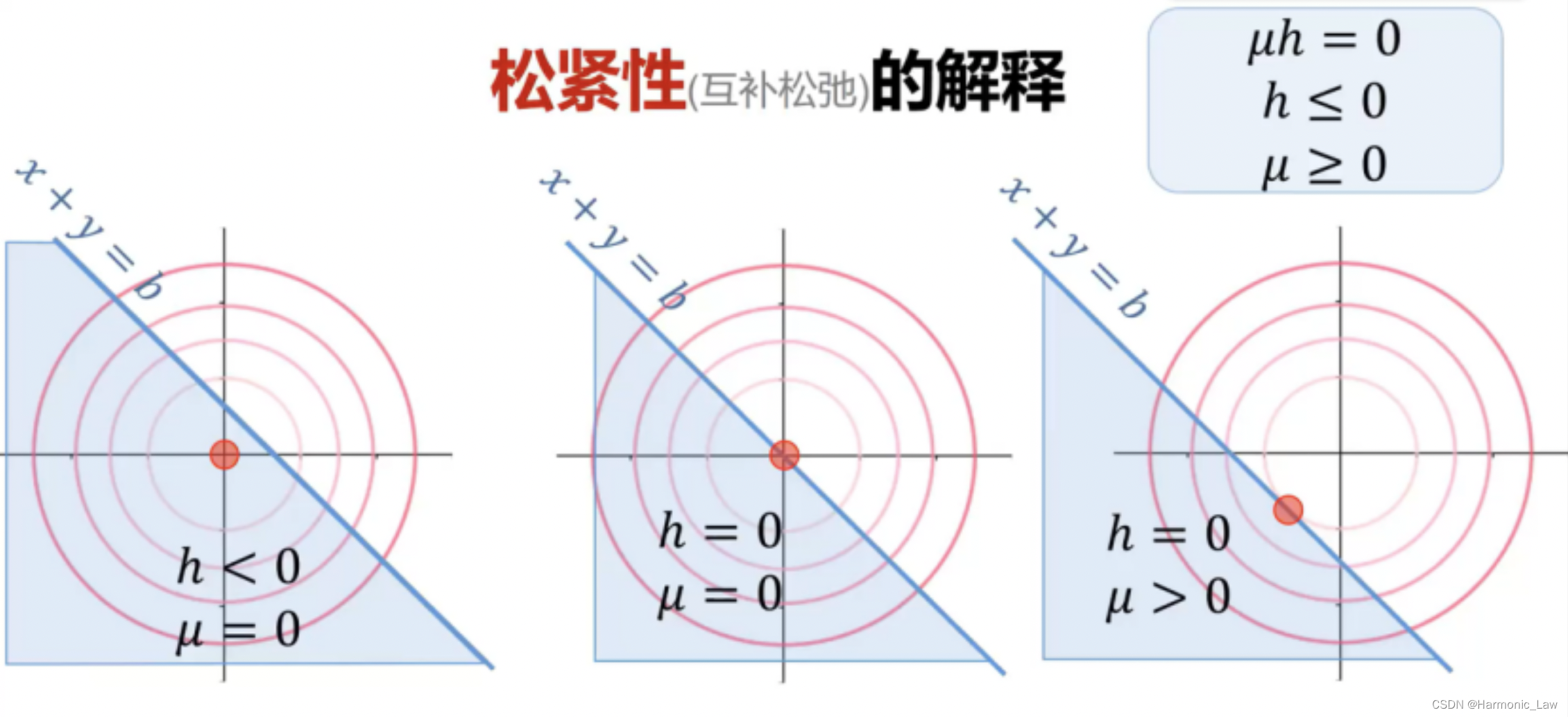
所以KKT条件如下：

$$\begin{array}{r}{\nabla }_{x}L(x^{\ast },{\lambda }^{\ast })=0\\ {\lambda }_i{g}_i(x^{\ast })=0\\ g_i(x^{\ast })\le 0\\ {\lambda }_i\ge 0\end{array}$$

3. 推广

更一般地，我们把等式约束也加进来，优化问题可以写为：

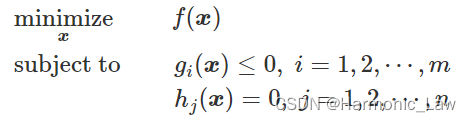
此时KKT条件为：

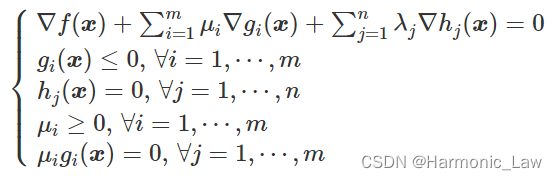
如果没有“不等式”约束条件，即$ m=0$，KKT条件就是拉格朗日乘数法中极值点满足的方程组。所以KKT条件是拉格朗日乘数法的推广，拉格朗日乘数法是KKT条件的特例。