第6章 支持向量机

6.1 间隔与支持向量

超平面的方程可以表示为：
$$w^{T}x+b=0\text{\hspace{1em}(6.1)}$$

推导6.1

样本数据集：
$$\left(\begin{array}{c}{x}_1^0,x_2^0,x_3^0,\dots ,x_m^0\\ x_1^1,x_2^1,x_3^1,\dots ,x_m^1\\ x_1^2,x_2^2,x_3^2,\dots ,x_m^2\\ x_1^3,x_2^3,x_3^3,\dots ,x_m^3\\ \dots \\ x_1^n,x_2^n,x_3^n,\dots ,x_m^n\end{array}\right)$$其中$x_n^m$表示第$m$个样本的第$n$个特征,这里对每一个样本添加一个$x_0=1$

$$\left(\begin{array}{c}{y}_1,y_2,y_3,\dots ,y_m\end{array}\right)$$其中$y_m$表示第$m$个样本的lable
$$w^T=\left(\begin{array}{c}{w}_0,w_1,w_2,w_3,\dots ,w_n\end{array}\right)$$，其中w为超平面的法向量,决定了超平面的方向，$w_0\ast x_0=b$为位移项，决定了超平面与原点之间的距离。

(6.2)
下面我们将超平面的方程标记为$(w,b)$,样本空间中任意点$x$到超平面$(w,b)$的距离可写为
$$r=\frac{|w^{T}x+b|}{||w||}\text{\hspace{1em}(6.2)}$$
推导(6.2)
在二维平面d怎么求？(点到直线的距离公式)
$(x,y)$到$Ax+By+C=0$的距离用以下公式表示
$$d=\frac{|Ax+By+C|}{\sqrt{A^2+B^2}}$$
拓展到n维空间有：$w^T{x}_b=0$→$w^{T}x+b=0$
$$||w||=\sqrt{w_1^2+w_2^2+\cdots +w_n^2}$$

假设超平面$(w,b)$能够将训练样本正确分类，即对于$(x_i,y_i)\in D$,若$y_i=+1$,则有$w^T{x}_i+b>0$;若$y_i=-1$,则有$w^T{x}_i+b<0$。
$$\{\begin{array}{ll}{w}^T{x}_i+b\ge +1& y_i=+1\\ w^T{x}_i+b\le -1& y_i=-1\end{array}\text{\hspace{1em}(6.3)}$$
推导6.3
空间任意一点到超平面的距离为d

$$d=\frac{|w^{T}x+b|}{||w||}$$
$$||w||=\sqrt{w_1^2+w_2^2+\cdots +w_n^2}$$

$$\{\begin{array}{ll}\frac{w^T{x}_i+b}{||w||}\ge d& \forall y_i=1\\ \frac{w^T{x}_i+b}{||w||}\le -d& \forall y_i=-1\end{array}⟹\{\begin{array}{ll}{w}_d^T{x}_i+b_d\ge 1& \forall y_i=1\\ w_d^T{x}_i+b_d\le -1& \forall y_i=-1\end{array}$$
其中$$\{\begin{array}{l}{w}_d^T=\frac{w^T}{d}\\ b_d=\frac{b}{d}\end{array}$$
对于决策边界的超平面方程：$w_d^{T}x+b_d=0$
重命名！！！ 令$$\{\begin{array}{l}{w}_d^T=w^T\\ b_d=b\end{array}⟹w^{T}x+b=0⟹\{\begin{array}{ll}{w}^T{x}_i+b\ge 1& \forall y_i=1\\ w^T{x}_i+b\le -1& \forall y_i=-1\end{array}$$
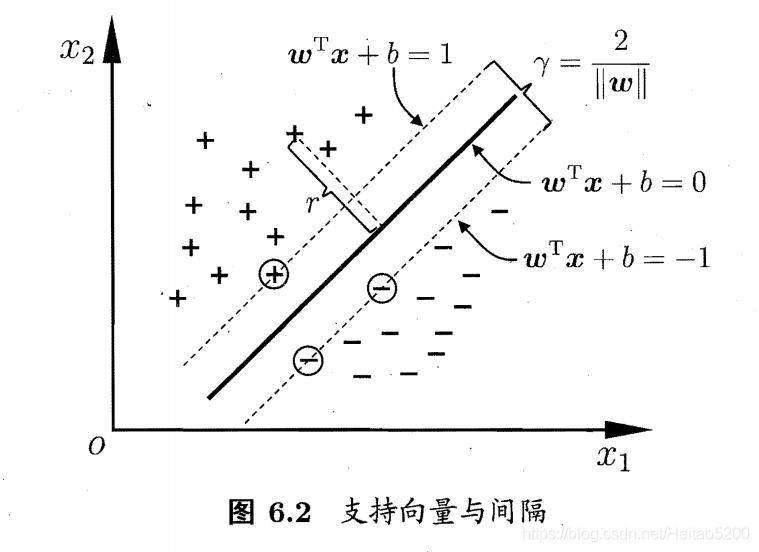
距离超平面最近的这几个训练样本点使式 (6.3) 的等号成立，它们被称为"支持向量" (surport vector)，两个异类支持向量到超平面的距离之和为:
$$\gamma =\frac{2}{||w||}\text{\hspace{1em}(6.4)}$$
推导6.4
在超平面的一边的同类支持向量构成决策边界方程为：
$$w^T{x}_i+b=1$$
超平面到该决策边界的距离为：
$$\gamma =\frac{1}{||w||}$$
两平行直线之间的距离

欲找到具有"最大间隔" (maximum margin) 的划分超平面，也就是要找
到能满足式 (6.3) 中约束的参数$w$和$b$,使得$\gamma$最大，即
$$\underset{\text{w,b}}{\underbrace{max}}\frac{2}{||w||}\text{\hspace{1em}(6.5)}$$

$$s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2\dots m$$
显然为了最大化间隔$\gamma$,仅需最大化$\frac{2}{||w||}$ ，这等价于最小化$||w||$ (加上系数与平方，只是为了计算方便)。
$$\underset{\text{w,b}}{\underbrace{min}}\frac{1}{2}||w|{|}^2\text{\hspace{1em}(6.6)}$$

$$s.t.y_i(w^T{x}_i+b)\ge 1,i=1,2\dots m$$

6.2 对偶问题

求解式 (6.6)来得到大间隔划分超平面所对应的模型
$$f(x)=w^{T}x+b\text{\hspace{1em}(6.7)}$$
对式 (6.6)使用拉格朗日乘子法可得到其"对偶问题" (dual problem). 具体来说，对式 (6.6) 的每条约束添加拉格朗日乘子$\alpha \ge 0$，则该问题的拉格朗日函数可写为:
$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))\text{\hspace{1em}(6.8)}$$
推导6.8
其中$\alpha =({\alpha }_1;{\alpha }_2;\cdots {\alpha }_m)$.令$L(w,b,\alpha )$对$w$和$b$的偏导为0​
$$\begin{array}{rl}L(w,b,\alpha )& =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))\\ & =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m({\alpha }_i-{\alpha }_i{y}_i{w}^T{x}_i+{\alpha }_i{y}_{i}b)\\ & =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i+\sum _{i=1}^m{\alpha }_i{y}_{i}b\end{array}$$
(1)对$w$和$b$分别求偏导数​

$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }^i{y}^i{x}^i=0⟹w=\sum _{i=1}^m{\alpha }^i{y}^i{x}^i$$

$$\frac{\partial L}{\partial b}=\sum _{i=1}^m{\alpha }^i{y}^{i}0⟹\sum _{i=1}^m{\alpha }^i{y}^i=0$$
$$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i\text{\hspace{1em}(6.9)}$$

$$0=\sum _{i=1}^m{\alpha }_i{y}_i\text{\hspace{1em}(6.10)}$$

$$L(w,b,\alpha )=\underset{\text{α}}{\underbrace{max}}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\text{\hspace{1em}(6.11)}$$
推导6.11
将式 (6.9)代人 (6.8) ，即可将$L(w,b,\alpha )$ 中的 $w$ 和 $b$ 消去,再考虑式 (6.10) 的约束,就得到式 (6.6) 的对偶问题
$$\begin{array}{rl}L(w,b,\alpha )& =\frac{1}{2}{w}^{T}w+\sum _{i=1}^m{\alpha }_i[1-y_i(w^T{x}_i+b)]\\ & =\frac{1}{2}{w}^{T}w+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-w^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b\\ & =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i-b\sum _{i=1}^m{\alpha }_i{y}_i\\ & =-\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^T(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i)+\sum _{i=1}^m{\alpha }_i-b\sum _{i=1}^m{\alpha }_i{y}_i\\ & =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i(x_i{)}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i-b\sum _{i=1}^m{\alpha }_i{y}_i⟹其中\sum _{i=1}^m{\alpha }_i{y}_i=0\\ & =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i(x_i{)}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{)}^T{x}_j\end{array}$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$

$${\alpha }_i\ge 0,i=1,2\dots ,m$$

将(6.9)带入$f(x)$得：
$$f(x)=w^{T}x+b=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^{T}x+b\text{\hspace{1em}(6.12)}$$
从对偶问题 (6.11)解出的${\alpha }_i$是式 (6.8) 中的拉格朗日乘子，它恰对应着训练样本 $(x_i,y_i)$. 注意到式 (6.6) 中有不等式约束,因此上述过程需满足KKT(Karush-Kuhn-Tucker) 条件,即要求:
$$\{\begin{array}{ll}{\alpha }_i\ge 0;& \\ y_{i}f(x_i)-1\ge 0;& \\ {\alpha }_i(y_{i}f(x_i)-1)=0& \end{array}\text{\hspace{1em}(6.13)}$$
使用$SMO$算法，固定${\alpha }_i,{\alpha }_j$以外的参数，则有：
$${\alpha }_i{y}_i+{\alpha }_j{y}_j=c,{\alpha }_i\ge 0,{\alpha }_j\ge 0\text{\hspace{1em}(6.14)}$$
$$c=-\sum _{k̸=i,j}{\alpha }_k{y}_k\text{\hspace{1em}(6.15)}$$
$${\alpha }_i{y}_i+{\alpha }_j{y}_j=c\text{\hspace{1em}(6.16)}$$
对于任何支持向量都有
$$\{\begin{array}{ll}{w}^T{x}_s+b=1& \forall y_s=1\\ w^T{x}_s+b=-1& \forall y_s=-1\end{array}⟹y_{s}f(x_s)=1$$
$$y_s(\sum _{i\in S}{\alpha }_i{y}_i{x}_i^T{x}_s+b)=1\text{\hspace{1em}(6.17)}$$
推导6.17
(6.17)等式两边同乘$y_s$
$$y_s^2(\sum _{i\in S}{\alpha }_i{y}_i{x}_i^T{x}_s+b)=y_s，其中y_s^2=1$$

$$b=\frac{1}{|S|}\sum _{s\in S}(y_s-\sum _{s\in S}{\alpha }_i{y}_i{x}_i^T{x}_s)\text{\hspace{1em}(6.18)}$$

6.3 核函数

$\varphi (x)$表示将 x映射
到一个合适的高维空间 后的特征向量
$$f(x)=w^T\varphi (x)+b\text{\hspace{1em}(6.19)}$$
$$\underset{\text{w,b}}{\underbrace{min}}\frac{1}{2}||w|{|}^2\text{\hspace{1em}(6.20)}$$

$$s.t.y_i(w^T\varphi (x_i)+b)\ge 1,i=1,2\dots m$$

$$\underset{\text{α}}{\underbrace{max}}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\varphi (x_i{)}^T(x_j)\text{\hspace{1em}(6.21)}$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$
$${\alpha }_i\ge 0,i=1,2,\dots ,m$$
半正定矩阵和正定矩阵
$$\kappa (x_i,x_j)=⟨\varphi (x_i),\varphi (x_j)⟩=\varphi (x)(x_i{)}^T\varphi (x)(x_j)\text{\hspace{1em}(6.22)}$$
$$\underset{\text{α}}{\underbrace{max}}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j\kappa (x_i,x_j)\text{\hspace{1em}(6.23)}$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$

$${\alpha }_i\ge 0,i=1,2\cdots ,m$$
$$\begin{array}{rl}f(x)& =w^T\varphi (x)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\varphi (x)(x_i{)}^T\varphi (x)+b\\ & =\sum _{i=1}^m{\alpha }_i{y}_i\kappa (x_i,x_j)+b\end{array}\text{\hspace{1em}(6.24)}$$
为核函数还可通过函数组合得到,例如:

• 若${\kappa }_1$和${\kappa }_2$为核函数，则对于任意正数${\gamma }_1$,${\gamma }_2$，其线性组合
  $${\gamma }_1{\kappa }_1+{\gamma }_2{\kappa }_2\text{\hspace{1em}(6.25)}$$
• 若${\kappa }_1$和${\kappa }_2$为核函数，则核函数的直积
  $${\kappa }_1⨂{\kappa }_2(x,z)={\kappa }_1(x,z){\kappa }_2(x,z)\text{\hspace{1em}(6.26)}$$
• 若${\kappa }_1$为核函 数，则对于任意函数$g(x)$，
  $$\kappa (x,z)=g(x){\kappa }_1(x,z)g(z)\text{\hspace{1em}(6.27)}$$

6.4 软间隔与正则化

$$y_i(w^T{x}_i+b)\ge 1,i=1,2\dots m\text{\hspace{1em}(6.28)}$$
$$\underset{\text{w,b}}{\underbrace{min}}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{l}_{0/1}(y_i(w^T{x}_i+b)-1)\text{\hspace{1em}(6.29)}$$
$$\begin{gathered} l_{0/1}(z)=\{\begin{array}{l} \\ 1,z<0\\ 0,otherwise\end{array}\text{\hspace{1em}(6.30)} \end{gathered}$$
在6.6式的基础上，我们把 不满足约束的样本以$l_{0/1}$损失函数引入进来 ,以实现允许少量样本不满足约束
hingle损失：$$l_{hinge}=max(0,1-z);\text{\hspace{1em}(6.31)}$$
指数损失：$$（exponentialloss）：l_{exp}(z)=exp(-z)\text{\hspace{1em}(6.32)}$$
对率损失：$$（logisticsloss）：L_{log}(z)=log(1+exp(-z))\text{\hspace{1em}(6.33)}$$
我们用hinge损失代替$l_{0/1}$ $$\underset{\text{w,b}}{\underbrace{min}}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^{m}max(0,1-y_i(w^T{x}_i+b))\text{\hspace{1em}(6.29)}$$

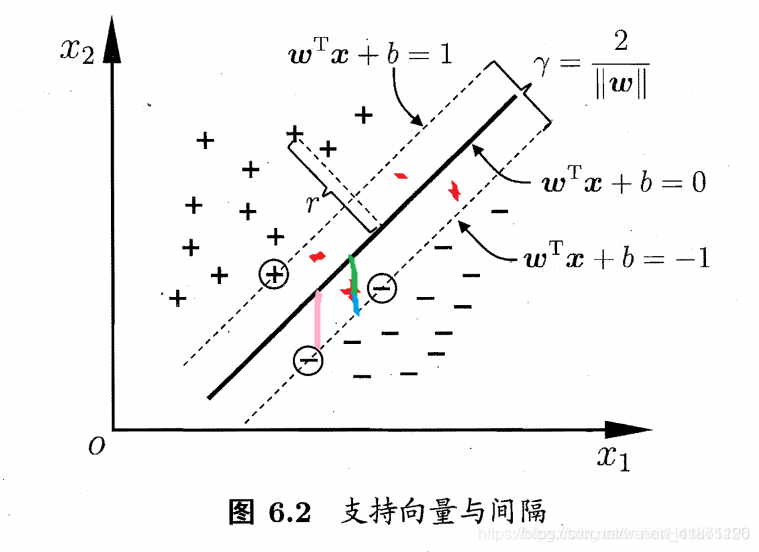
引入“松弛变量”${\epsilon }_i$,为了方便理解，我们用‘红色’标出四个位于间隔内的点，粉色线段长度代表函数间隔（在这里为1）蓝色线段为$\epsilon$ 绿色线段为$1-\epsilon$ ，此时我们将（6.34）重写为$$\underset{\text{w,b,εi}}{\underbrace{min}}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\epsilon }_i\text{\hspace{1em}(6.35)}$$ $$s.t.y_i(w^T{x}_i+b)\ge 1-{\epsilon }_i,i=1,2\dots m$$ $${\epsilon }_i\ge 0i=1,2,...m.$$

$$L(w,b,\alpha ,\epsilon ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\epsilon }_i+\sum _{i=1}^m{\alpha }_i(1-{\epsilon }_i-y_i(w^T{x}_i+b))-\sum _{i=1}^m{\mu }_i{\epsilon }_i\text{\hspace{1em}(6.36)}$$在这部分由于存在两个月叔条件，我们引入两个拉格朗日乘子$\alpha ,\epsilon$
分别对$w,b,\epsilon$求导并使其为0
$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }^i{y}^i{x}^i=0⟹w=\sum _{i=1}^m{\alpha }^i{y}^i{x}^i\text{\hspace{1em}(6.37)}$$

$$\frac{\partial L}{\partial b}=\sum _{i=1}^m{\alpha }^i{y}^i=0⟹\sum _{i=1}^m{\alpha }^i{y}^i=0\text{\hspace{1em}(6.38)}$$
​
$$\frac{\partial L}{\partial \epsilon }=C\sum _{i=1}^{m}1-\sum _{i=1}^m{\alpha }_1-\sum _{i=1}^m{u}_i⟹C={\alpha }_i+{\mu }_i\text{\hspace{1em}(6.39)}$$

将式6.37-6.39代入6.36可以得到6.35的对偶问题——线性规划中普遍存在配对现象，每一个线性规划问题都存在另一个与他有对应关系的线性规划问题，其一叫原问题，其二叫对偶问题
$$\begin{array}{rl}L(w,b,\alpha ,\epsilon ,\mu )& =\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{\epsilon }_i+\sum _{i=1}^m{\alpha }_i(1-{\epsilon }_i-y_i(w^T{x}_i+b))-\sum _{i=1}^m{\mu }_i{\epsilon }_i\\ & =\frac{1}{2}||w|{|}^2+\sum _{i=1}^m{\alpha }_i(1-y_i(w^T{x}_i+b))+C\sum _{i=1}^m{\epsilon }_i-\sum _{i=1}^m{\alpha }_i{\epsilon }_i-\sum _{i=1}^m{\mu }_i{\epsilon }_i\\ & =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i(x_i{)}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i+\sum _{i=1}^{m}C{\epsilon }_i-\sum _{i=1}^m{\alpha }_i{\epsilon }_i-\sum _{i=1}^m{\mu }_i{\epsilon }_i\\ & =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i(x_i{)}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i+\sum _{i=1}^m(C-{\alpha }_i-{\mu }_i){\epsilon }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{)}^T{x}_j\\ & \underset{\alpha }{\underbrace{max}}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i{)}^T{x}_j\\ & s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le Ci=1,2,\dots ,m\end{array}\text{\hspace{1em}(6.40)}$$

KKT条件，这里简单提一下不等式约束的KKT拉格朗日乘子为$\alpha$不等式约束为$\epsilon$那么要满足$$\{\begin{array}{l}\alpha \ge 0\\ \epsilon \\ \alpha \epsilon =0\end{array}$$
$$\{\begin{array}{l}{\alpha }_i\ge 0,{\mu }_i\ge 0,\\ y_{i}f(x_i)-1+{\epsilon }_i\ge 0,\\ {\alpha }_i(y_{i}f(x_i)-1+{\epsilon }_i)=0,\\ {\epsilon }_i\ge 0,{\mu }_i{\epsilon }_i=0.\end{array}\text{\hspace{1em}(6.41)}$$

我们对不同的损失函数概括抽象推广到一般形式：
$$\underset{f}{\underbrace{min}}\Omega (f)+C\sum _{i=1}^{m}l(f(x_i),y_i)\text{\hspace{1em}(6.42)}$$

6.5 支持向量回归

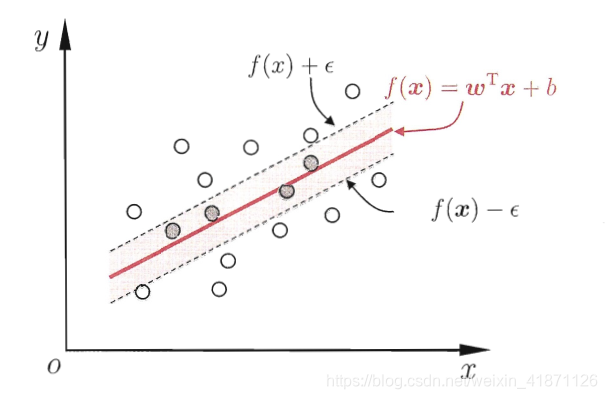
在这里简单说一点，我们如何来看待分类和回归，分类的损失函数要么是1，要么是0，回归得的损失函数是连续的数值。支持向量回归我们容忍$f(x)$与y之间有$ϵ$的误差,（结合图片，把6.43,6.44一起理解）
$$\underset{\text{w,b,εi}}{\underbrace{min}}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m{l}_{ϵ}(f(x_i)-y_i)\text{\hspace{1em}(6.43)}$$ $$\begin{gathered} l_{ϵ}(z)=\{\begin{array}{l} \\ 0,if|z|\le ϵ\\ |z|-ϵ,otherwise\end{array}\text{\hspace{1em}(6.44)} \end{gathered}$$

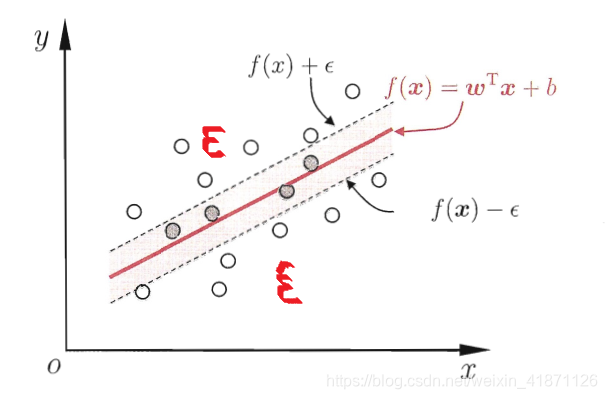
如图所示我们在间隔两侧引入松弛变量$\epsilon ,\hat{\epsilon }$,就是在间隔$ϵ$基础上我们重新增加了一部分“容忍量”
$$\underset{\text{w,b,εi,ε^i}}{\underbrace{min}}\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m({ϵ}_i,{\hat{\epsilon }}_i\text{\hspace{1em}(6.45)}$$ $$f(x_i)-y_i\le ϵ+{\epsilon }_i,$$ $$y_i-f(x_i)\le ϵ+{\hat{\epsilon }}_i,$$ $${\epsilon }_i\ge 0,\hat{\epsilon }0,i=1,2,\dots ,m.$$

引入拉格朗日乘子${\mu }_i\ge 0,m{\hat{\mu }}_i\ge 0$,对应两个松弛变量，$\alpha -i\ge 0,{\hat{\alpha }}_i\ge 0$对应两个约束条件.
$$\begin{gathered} L(w,b,\alpha ,\hat{\alpha },\epsilon ,\hat{\epsilon },\mu ,\hat{\mu }) \\ =\frac{1}{2}||w|{|}^2+C\sum _{i=1}^m({\epsilon }_i+{\hat{\epsilon }}_i)-\sum _{i=1}^m{\mu }_i{\epsilon }_i-\sum _{i=1}^m{\hat{\mu }}_i{\hat{\epsilon }}_i+\sum _{i=1}^m{\alpha }_i(f(x_i)-y_i-ϵ-{\epsilon }_i)+\sum _{i=1}^m{\hat{\alpha }}_i(y_i-f(x_i)-ϵ-{\hat{\epsilon }}_i\text{\hspace{1em}(6.46)} \end{gathered}$$

$L(w,b,\alpha ,\hat{\alpha },\epsilon ,\hat{\epsilon },\mu ,\hat{\mu })$分别对 $w，b,\epsilon ,\hat{\epsilon }$求偏导并使其为0
$$\frac{\partial L}{\partial w}=w-\sum _{i=1}^m{\alpha }_i{x}_i-\sum _{i=1}^m{\hat{\alpha }}_i{x}_i=0⟹w=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i\text{\hspace{1em}(6.47)}$$ $$\frac{\partial L}{\partial b}=\sum _{i=1}^m{\alpha }_i-\sum _{i=1}^m{\hat{\alpha }}_i=0⟹0=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)\text{\hspace{1em}(6.48)}$$ $$\frac{\partial L}{\partial {\epsilon }_i}=C\sum _{i=1}^{m}1-\sum _{i=1}^m{\alpha }_1-\sum _{i=1}^m{u}_i⟹C={\alpha }_i+{\mu }_i\text{\hspace{1em}(6.49)}$$ $$\frac{\partial L}{\partial {\hat{\epsilon }}_i}=C\sum _{i=1}^{m}1-\sum _{i=1}^m{\hat{\alpha }}_1-\sum _{i=1}^m{\hat{\mu }}_i⟹C={\hat{\alpha }}_i+{\hat{\mu }}_i\text{\hspace{1em}(6.50)}$$

将6.47-6.50代入6.46，即可得到SVR的对偶问题
$$\begin{array}{r}L(w,b,\alpha ,\hat{\alpha },\epsilon ,\hat{\epsilon },\mu ,\hat{\mu })=-\frac{1}{2}{w}^T\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i+\sum _{i=1}^m({\alpha }_i{\epsilon }_i+{\alpha }_i{\hat{\epsilon }}_i+{\mu }_i{\epsilon }_i+{\mu }_i{\hat{\epsilon }}_i-{\mu }_i{\epsilon }_i-{\hat{\mu }}_i{\hat{\epsilon }}_i)\\ +\sum _{i=1}^m{\alpha }_i((w^T{x}_i+b)-y_i-ϵ-{\epsilon }_i)+\sum _{i=1}^m{\hat{\alpha }}_i(y_i-(w^T+b)-ϵ-{\hat{\epsilon }}_i)\\ =\sum _{i=1}^m({\alpha }_i{\epsilon }_i+{\alpha }_i{\hat{\epsilon }}_i+{\mu }_i{\epsilon }_i+{\mu }_i{\hat{\epsilon }}_i-{\mu }_i{\epsilon }_i-{\hat{\mu }}_i{\hat{\epsilon }}_i-{\mu }_i{\epsilon }_i-{\hat{\mu }}_i{\hat{\epsilon }}_i-{\alpha }_i{\epsilon }_i-{\hat{\alpha }}_i{\hat{\epsilon }}_i)\\ +\sum _{i=1}^m[y_i({\hat{\alpha }}_i-{\alpha }_i)-ϵ({\hat{\alpha }}_i+{\alpha }_i)]-\frac{1}{2}{w}^T\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i+\sum _{i=1}^m({\alpha }_i-{\hat{\alpha }}_i)w^T{x}_i\\ =\sum _{i=1}^m[y_i({\hat{\alpha }}_i-{\alpha }_i)-ϵ({\hat{\alpha }}_i+{\alpha }_i)]+\sum _{i=1}^m({\alpha }_i{\hat{\epsilon }}_i-{\mu }_i{\hat{\epsilon }}_i-{\hat{\mu }}_i{\hat{\epsilon }}_i-{\hat{\alpha }}_i{\hat{\epsilon }}_i)-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-{\alpha }_i)(\widehat{|}alph{a}_j-{\alpha }_j)x_i^T{x}_j\\ =\sum _{i=1}^m[y_i({\hat{\alpha }}_i-{\alpha }_i)-ϵ({\hat{\alpha }}_i+{\alpha }_i)]+\sum _{i=1}^m[({\alpha }_i+{\mu }_i)-({\hat{\mu }}_i+{\hat{\alpha }}_i)]{\hat{\epsilon }}_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-{\alpha }_i)(\widehat{|}alph{a}_j-{\alpha }_j)x_i^T{x}_j\\ =\sum _{i=1}^m[y_i({\hat{\alpha }}_i-{\alpha }_i)-ϵ({\hat{\alpha }}_i+{\alpha }_i)]-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-{\alpha }_i)(\widehat{|}alph{a}_j-{\alpha }_j)x_i^T{x}_j\end{array}$$ $$\sum _{i=1}^m[y_i({\hat{\alpha }}_i-{\alpha }_i)-ϵ({\hat{\alpha }}_i+{\alpha }_i)]-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m({\hat{\alpha }}_i-{\alpha }_i)(\widehat{|}alph{a}_j-{\alpha }_j)x_i^T{x}_j\text{\hspace{1em}(6.51)}$$ $$s.t.\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)=0$$ $$0\le {\alpha }_i,{\hat{\alpha }}_i\le C$$

上述过程满足KKT条件，即要求
$$\begin{gathered} \{\begin{array}{l} \\ {\alpha }_i(f(x_i)-y_i-ϵ-{\epsilon }_i)=0\\ {\hat{\alpha }}_i(y_i-f(x_i)-ϵ-{\epsilon }_i)=0\\ {\alpha }_i{\hat{\alpha }}_i=0,{\epsilon }_i{\hat{\epsilon }}_i=0\\ (C-{\alpha }_i){\epsilon }_i=0,(c-{\hat{\alpha }}_i){\hat{\epsilon }}_i=0\end{array}r\text{\hspace{1em}(6.52)} \end{gathered}$$

将式6.47代入6.7
$$f(x)=w^{T}x+b\text{\hspace{1em}(6.7)}$$ $$w=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i\text{\hspace{1em}(6.47)}$$ $$f(x)=\sum _{i=1}^m({\hat{\alpha }}_i-{\alpha }_i)x_i^{T}x+b\text{\hspace{1em}(6.53)}$$

$$b=y_i+ϵ-\sum _{j=1}^m({\hat{\alpha }}_j{\alpha }_j)x_j^T{x}_i\text{\hspace{1em}(6.54)}$$