素数

素数（又称质数），指在大于1的自然数中，除了1和它本身以外，不能被其他其它自然数整除的数。与之相对应的是合数，合数除了1和它本身以外还可以被其他自然数整除。（1既不是质数也不是合数）。

问题背景：

讨论如何筛选出2~n之间的所有素数。

试除法：

如何判断i是否为质数：基于定义，用区间[2,i-1]中的每一个数对i进行试探，若区间中存在可以整除i的数，则i为合数。反之为质数。

/ /代码一：
bool is_prime(int i){
if(i<2) return false;
for(int j=2;j<i;j++)
 if(i%j==0) return false;
 return true;
}

假设a*b=i，且a<=b,那么a必然小于等于sqrt(i),所以没有必要用大于sqrt(i)的数进行试探，故以上方法可以优化如下：

/ /代码二：
bool is_prime(int i){
if(i<2) return false;
for(int j=2;j<=sqrt(i);j++)
 if(i%j==0) return false;
 return true;
}

代码二的优化思想也可以写成这样：

bool is_prime(int i){
if(i<2) return false;
for(int j=2;j*j<=i;j++)
 if(i%j==0) return false;
 return true;
}

在“讨论如何筛选出2~n之间的所有素数”的问题背景下，试除法的时间复杂度较高。

埃氏筛法

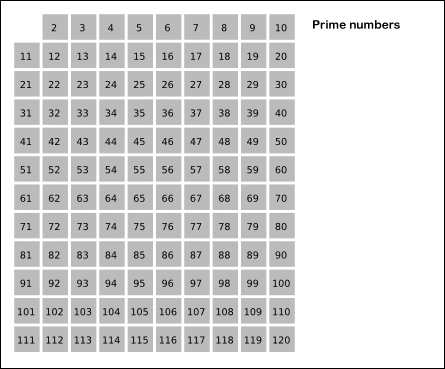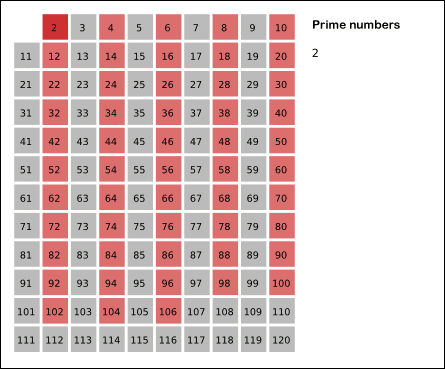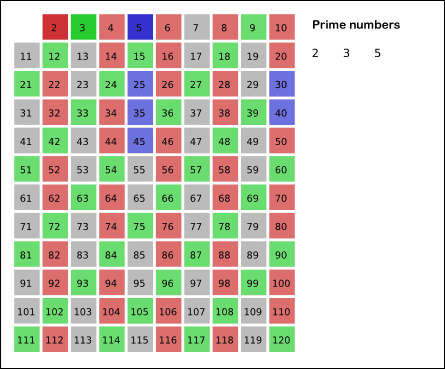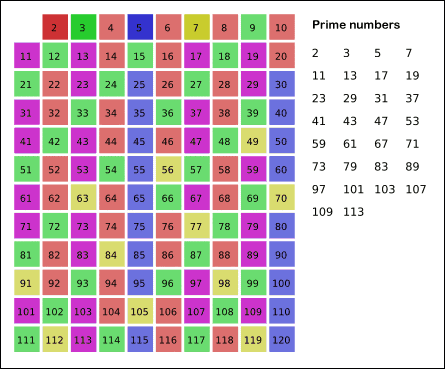
埃氏筛法的思想：任意素数x(x>=2)的倍数2x,3x,…都不是素数。基于这个思想，从小到大依次枚举区间[2,n]中的整数，将素数的倍数标记为合数，没有被标记的数即为质数。

  bool vis[maxn]; / / vis[i]为true表示i为质数
  int primes[maxn]; / /primes中存素数，下标从0开始
  int countPrimes(int n) { / /返回[2,n]之间素数的个数
  if(n<=2) return 0;
  int cnt=0;   / /cnt记录素数的个数
  for(int i=2;i<=n;i++)
  {
  if(vis[i]){
  primes[cnt]=i; / /i为素数就添加到primes中，
  cnt++;         / /素数个数cnt增加
  for(int j=i+i;j<=n;j+=i)
  vis[j]=false; / /i的倍数j都是合数,标记为false
  }
 }
     return cnt;      
   }
/ /函数返回[2,n]之间素数的个数，primes中存素数，下标从0开始
/ /vis 中“有用信息”为vis[2~n],因为vis数组初始化为了true

我们发现上面的做法会有很多重复标记的情况，例如6被2和3标记了两次，15被3和5标记了两次。实际上，小于i² 的i的倍数在扫描更小的数的时候就已经被标记过了。所以，对于每一个质数i只需要标记大于i² 的倍数即可。故最终优化的埃氏筛法如下：

  bool vis[maxn]; 
  int primes[maxn]; 
  int countPrimes(int n) { 
  if(n<=2) return 0;
  int cnt=0;  
  for(int i=2;i<=n;i++)
  {
  if(vis[i]){
  primes[cnt]=i; 
  cnt++;         
  for(int j=i*i;j<=n;j+=i)   / /i+i改为i*i,其余同上
  vis[j]=false; 
  }
 }
     return cnt;      
   }

附上一张埃氏筛法图解（图片来源于网络）：

埃氏筛法的时间复杂度为O(nloglogn)，其中还是存在一些重复标记的情况。下面引入线性时间复杂度的欧拉筛法.

欧拉筛法：

欧拉筛的基本操作过程：
1.同样从小到大依次判断[2,n]中的整数是否素数：vis[i]为true表示i为质数，false表示i为合数。i为质数就将其添加到primes数组中。
2.对于每个i，我们从当前的primes数组中从小到大挑选素数，将i*primes[j]标记为合数。直到i中含有质因子primes[j]的时候，就停止这个挑选素数primes[j]标记i*primes[j]的过程。如此，当i为n时，就能不重不漏地将[2,n]中的素数和合数标记出来。由于每个数都只被它的最小质因子标记一次，所以这个算法的时间复杂度为O(n)。

个人对欧拉筛法的理解：
欧拉筛法基于算术基本定理，定理描述如下：
由欧拉筛的“操作过程”，可以得到：
1.若当前i为质数，即i=$P_x$ ，那么$P_x$可以筛去合数$P_1{P}_x$、$P_2{P}_x$、$P_3{P}_x$、…、$P_{x-1}{P}_x$、$P_x^2$ 。
2.若当前合数i=$P_x^{c_x}{P}_y^{c_y}$，则$P_x^{c_x}{P}_y^{c_y}$可以筛掉$P_1{P}_x^{c_x}{P}_y^{c_y}$、$P_2{P}_x^{c_x}{P}_y^{c_y}$、$P_3{P}_x^{c_x}{P}_y^{c_y}$、…、$P_{x-1}{P}_x^{c_x}{P}_y^{c_y}$、$P_x^{c_x+1}{P}_y^{c_y}$。
3.若当前合数i=$P_x^{c_x}{P}_y^{c_y}{P}_z^{c_z}$，则$P_x^{c_x}{P}_y^{c_y}{P}_z^{c_z}$可以筛掉$P_1{P}_x^{c_x}{P}_y^{c_y}{P}_z^{c_z}$、$p_2{P}_x^{c_x}{P}_y^{c_y}{P}_z^{c_z}$、$p_3{P}_x^{c_x}{P}_y^{c_y}{P}_z^{c_z}$、…、$p_{x-1}{P}_x^{c_x}{P}_y^{c_y}{P}_z^{c_z}$、$P_x^{c_x+1}{P}_y^{c_y}{P}_z^{c_z}$ 。
4.上面3中的质数个数可以不断扩充，即该情况可以推广到很多个质数相乘的情况。以当前数i为基础，将小于等于$P_x$（$P_x$为i的最小质因子）的质数与i相乘得到的数筛掉。
5.由算术基本定理可以看出，[2,n]之间的整数被质数以及有限个质数的乘积“没有遗漏地覆盖”。
6.i筛掉的都是大于i的合数。由以上几条论述可以知道，当i遍历到n的时候，[2,n]之间的合数就会被全部标记，没有一个合数会被遗漏。且每个合数都只被标记一次，故时间复杂度为O(n)。
欧拉筛法代码：

  bool vis[maxn];    / / vis[i]为true表示i为质数
  int primes[maxn];   / /primes中存素数，下标从0开始
int countPrimes(int n) {   / /返回[2,n]之间素数的个数
    if(n<=2) return 0;
    int cnt=0;      / /cnt记录素数的个数
    for(int i=2;i<=n;i++)
    {
    if(vis[i]) {primes[cnt]=i;cnt++;}  / /当前数i为质数，添加到primes数组中
     for(int j=0;j<cnt;j++){
      if(primes[j]*i>=n) break;  / /标记的数超过n就跳出循环
      vis[primes[j]*i]=false;   / /标记合数
      if(i%primes[j]==0) break; / /primes[j]为i的质因子且Primes[j]大于Px,停止用i标记后面的数
     }
     }
     return cnt;    
     }
/ /函数返回[2,n]之间素数的个数，primes中存素数，下标从0开始
/ /vis 中“有用信息”为vis[2~n],因为vis数组初始化为了true

模板题：leetcode 204. 计数质数

题目描述：

统计所有小于非负整数 n 的质数的数量。
示例:
输入: 10
输出: 4
解释: 小于 10 的质数一共有 4 个, 它们是 2, 3, 5, 7 。
来源：力扣（LeetCode）
题目链接：https://leetcode-cn.com/problems/count-primes/

AC代码：

class Solution {
public:
    int countPrimes(int n) {
    if(n<=2) return 0;
    vector<bool>vis(n,true); 
    vector<int>primes;
    int cnt=0;
    for(int i=2;i<n;i++)
    {
    if(vis[i]) {primes.push_back(i);cnt++;}
     for(int j=0;j<cnt;j++){
      if(primes[j]*i>=n) break;
      vis[primes[j]*i]=false;
      if(i%primes[j]==0) break;     
     }
     }
     return cnt;    
     }
     };

上一篇博客：牛客网 64位整数乘法