博主推荐！！！： "近期我偶然邂逅了一个极为出色的人工智能学习平台，它不仅内容深入浅出，讲解方式还风趣幽默，让人学习起来既轻松又高效。如此宝藏资源，我迫不及待想要与各位共享，让我们一起进入这个精彩纷呈的学习网站吧！"即刻点击https://www.captainbed.cn/cyy

算法系列:今天，我们要聊的是一种超级强大的算法策略——分治算法（Divide and Conquer）。它就像一把魔法棒🔮，能把复杂的大问题分解成一堆小问题，再逐个🐔破，最后合并成原问题的解。

一、分治算法是什么？                                                                           

分治算法，简单来说，就是一种解决问题的策略。它通过将一个大问题分解成若干个较小的、相似或相同的子问题，递归地解决这些子问题，然后将子问题的解合并起来，从而得到原问题的解。

这个魔法过程可以概括为三个步骤：

分解（Divide）：将原问题分解成若干个规模更小的子问题。这些子问题相互独立，并且与原问题形式相同。
解决（Conquer）：递归地解决这些子问题。如果子问题的规模足够小，则直接求解。
合并（Combine）：将子问题的解合并为原问题的解。

二、分治算法的经典应用                                                                          

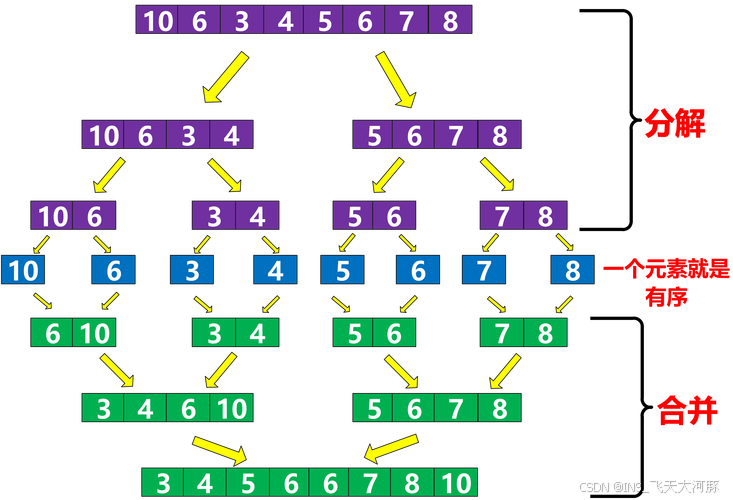
1. 归并排序（Merge Sort）                                                                                       

归并排序是分治策略的典型应用之一。它的基本思想是：将数组分成两半，递归地对每一半进行排序，然后将排序好的两半合并。

具体步骤如下：

分解：递归地将原数组（原问题）划分为两个子数组（子问题），直到子数组只剩一个元素（最小子问题）。
解决：每个子数组只有一个元素时，自然是有序的，因此不需要再排序。
合并：从底至顶地将有序的子数组（子问题的解）进行合并，从而得到有序的原数组（原问题的解）。

归并排序的时间复杂度为O(n log n)，非常高效！

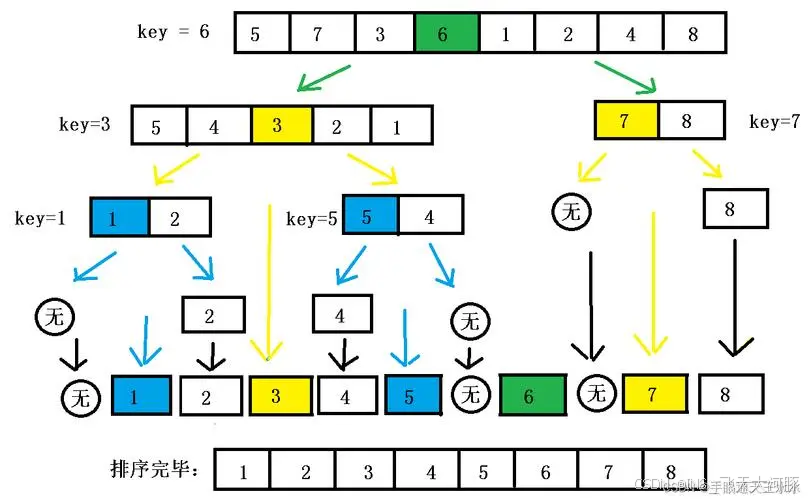
2. 快速排序（Quicksort）                                                                                         

快速排序是另一种基于分治策略的排序算法。它的基本思想是：选取一个基准值，将数组分为小于基准和大于基准的两部分，然后递归地对这两部分进行排序。

具体步骤如下：

分解：选取一个基准值，将数组分成两部分，一部分包含所有小于基准的元素，另一部分包含所有大于基准的元素。
解决：递归地对这两部分进行排序。
合并：由于快速排序在分解的过程中已经实现了部分排序，因此不需要额外的合并步骤。排序完成后，整个数组就是有序的。

快速排序的平均时间复杂度也是O(n log n)，但在最坏情况下会退化到O(n^2)。不过，由于它的实现简单且大多数情况下效率较高，因此在实际应用中非常受欢迎。

3. 二分查找（Binary Search）                                                                                  

二分查找是一种高效的查找算法，它适用于在有序数组中查找特定元素。二分查找也基于分治策略。

具体步骤如下：

分解：将有序数组从中点索引分为两部分。
解决：根据目标值与中间元素值的比较结果，决定排除哪一半区间，然后在剩余区间执行相同的二分操作。
合并：二分查找旨在查找一个特定元素，因此不需要将子问题的解进行合并。当子问题得到解决时，原问题也会同时得到解决。二分查找的时间复杂度为O(log n)，非常高效！

三、分治算法的其他应用

除了排序和查找，分治算法还可以应用于许多其他领域。

1. 大整数乘法

对于非常大的整数相乘，直接计算可能会超出计算机的表示范围。这时，我们可以使用分治策略，将大整数分成较小的部分进行乘法运算，然后合并结果。

EG：Karatsuba算法就是一种基于分治策略的大整数乘法算法。它将两个大整数分成两半，然后分别计算三个较小的乘积（两个半数的乘积、两个半数的和与另一个半数的乘积），最后通过这三个乘积计算出原问题的解。

2. 矩阵乘法

矩阵乘法是计算线性代数中的一个基本操作。对于大规模的矩阵相乘，直接计算可能会非常耗时。这时，我们可以使用分治策略，将矩阵分成较小的块进行乘法运算，然后合并结果。

EG：Strassen算法就是一种基于分治策略的矩阵乘法算法。它将两个大矩阵分成四个小块，然后分别计算七个较小的乘积（六个块与块的乘积和一个块与自身和的乘积），最后通过这七个乘积计算出原问题的解。

3. 汉诺塔问题

汉诺塔问题是一个经典的递归问题。它的基本思想是：将n个盘子从一个柱子移动到另一个柱子，且每次只能移动一个盘子，并且不能把大盘子放在小盘子上面。这个问题可以视为典型的分治策略。我们可以将问题分解成n-1个盘子从一个柱子移动到另一个柱子（借助第三个柱子），然后将第n个盘子移动到目标柱子，最后再将n-1个盘子从第三个柱子移动到目标柱子（借助源柱子）。通过递归地解决这些子问题，最终可以得到原问题的解。

四、分治算法的效率与并行优化

分治算法的效率通常取决于如何分解问题以及如何合并子问题的解。在某些情况下，分治算法可以显著减少问题解决的时间复杂度。

此外，分治算法还非常适合并行优化。由于子问题通常是独立的，因此可以并行地解决这些子问题。在多核或多处理器的环境中，系统可以同时处理多个子问题，从而显著减少总体的运行时间。

例如，在归并排序中，我们可以将数组分成多个子数组，并在不同的处理器上并行地对这些子数组进行排序。排序完成后，再将各个子数组合并成一个有序数组。这样，就可以充分利用计算资源，提高排序效率。

五、分治算法在生活中的应用

分治算法不仅适用于算法领域，还可以应用于生活中的各个方面。

1. 时间管理

当我们面临很多任务和项目时，可以使用分治法来合理安排和管理时间。首先，将任务分解为小的子任务，然后按照优先级和紧急程度进行排序。接下来，将时间分配给每个子任务，并设置合理的截止日期。最后，按照计划执行，完成每个子任务，最终完成整个项目。

2. 减轻压力

压力是生活中常见的问题。我们可以使用分治法来减轻压力。首先，分析和确定压力源，找出造成压力的具体原因。然后，将压力源分解为小的问题，一一解决。可以采取合理的时间管理、寻求帮助、调整心态等方法，逐步解决每一个小问题，从而逐渐减轻整体的压力。

3. 学习方法

在学习过程中，分治法也可以起到很好的帮助作用。面对一个复杂的知识点或者大量的学习内容，我们可以将其分解为小的知识点或者小的学习任务。然后，专注地学习每个小的部分，理解和掌握后再逐步整合到整体。这样做可以避免学习过程过于繁琐和困难，提高效率和学习成果。

4. 健康管理

对于保持健康也可以采用分治法。针对身体健康的问题，可以将其分解为饮食、运动、休息等方面。然后，分别制定相应的健康计划和目标，例如规律饮食、每周锻炼几次等。接着，逐步实践和改进每个小的目标，最终达到整体的健康管理。

六、总结

分治算法是一种非常强大且常见的算法策略。它通过将一个大问题分解成若干个较小的、相似或相同的子问题，递归地解决这些子问题，然后将子问题的解合并起来，从而得到原问题的解。这个过程可以显著提高算法的效率，并且非常适合并行优化。在算法领域，分治算法被广泛应用于排序、查找、大整数乘法、矩阵乘法等领域。此外，分治算法还可以应用于生活中的各个方面，如时间管理、减轻压力、学习方法和健康管理等。