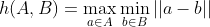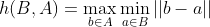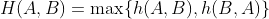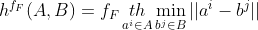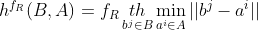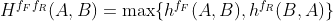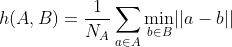Hausdorff 距离

Hausdorff 距离是描述两组点集之间相似程度的一种量度；

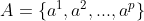
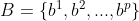
假设有两组集合： $A=\{a^1,a^2,...,a^p\}$ ， $B=\{b^1,b^2,...,b^p\}$ ；

则这两个点集之间的单向 Hausdorff 距离：

$h(A,B)=\max\limits_{a \in A} \min\limits_{b \in B}||a-b||$

$h(B,A)=\max\limits_{b \in A} \min\limits_{a \in B}||b-a||$

其中，||a-b|| 表示 a 与 b 之间的欧氏距离，h(A,B) 也叫前向 Hausdorff 距离，h(B,A) 也叫后向 Hausdorff 距离;

h(A,B) 的理解：先在集合 B 中取距离集合 A 最近的点，然后计算集合 A 中的每个点与之间的距离，并将距离进行排序，然后取距离最大的值作为 h(A,B) 的值。（若 h(A,B)=d，表示 A 中所有点到 B 集合的距离不超过 d）

双向 Hausdorff 距离： $H(A,B)=\max\{h(A,B),h(B,A)\}$

双向 Hausdorff 距离取单向 Hausdorff 距离中的最大值，度量了两个点集间的不相似程度（双向 Hausdorff 距离越小，匹配程度越高）；

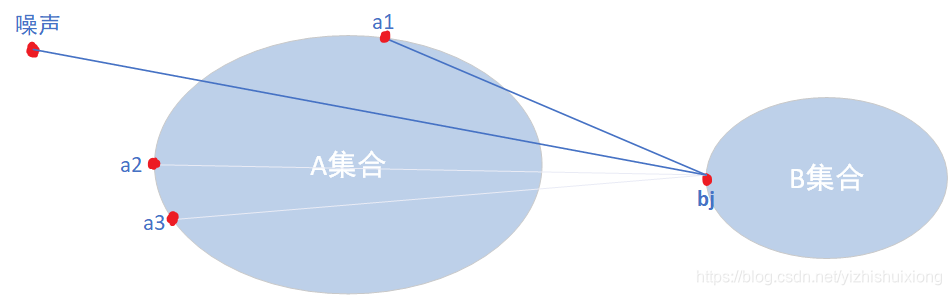
但是，在图像存在噪声污染或遮挡等情况时，上述的 Hausdorff 距离很容易造成误匹配，如下图：

B 集合中距离 A 集合最近的点 bj，A集合中距离 bj 最远的点是 a2，但是由于存在噪声，Hausdorff 距离并没有取 a2 与 bj 之间的距离，而是噪声与 bj 之间的距离，导致错误。

为了解决这一问题，Huttenlocher 提出了部分 Hausdorff 距离；

部分单向 Hausdorff 距离：

$h^{f_F}(A,B)=f_F \mathop{th} \limits_{a^i\in A}\min\limits_{b^j \in B}||a^i-b^j||$

$h^{f_R}(B,A)=f_R \mathop{th} \limits_{b^j \in B}\min\limits_{a^i\in A}||b^j-a^i||$

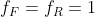
其中， $f_F,f_R \in [0,1]$ 分别称为前向分数和后向分数，控制着前向距离和后向距离；th 表示排序。（当 f_F=f_R=1 时，该公式退化为原始的 Hausdorff 距离）

部分双向 Hausdorff 距离：

$H^{f_F f_R}(A,B)=\max\{h^{f_F }(A,B),h^{f_R}(B,A)\}$

在论文《基于Hausdorff距离的手势识别》中提出了一种修正的 Hausdorff 距离（Modified Hausdorff Distance，MHD）：

$h(A,B)=\frac{1}{N_A}\sum\limits_{a\in A}{\min\limits_{b\in B}}||a-b||$

其中， N_A 是 A 集合中点的个数；

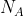
在此论文中也证明了 MHD 对噪声不太敏感，可以避免由于部分噪声像素点的干扰带来的偏差；

并且，相比于用原始的 Hausdorff 距离对手势进行匹配识别，修正的 Hausdorff 距离具有明显的优越性；使用这种距离在测试集上的平均识别率达96.7%。