• （一）问题描述

设B是一个n*n棋盘，n=2^k(k=1，2，3……)。用分治算法设计一个算法，使得：用若干个L型条块可以覆盖住B的除一个特殊方块外的所有方格。其中，一个L型条块可以覆盖3个方格。且任意两个L型条块不能重叠覆盖棋盘。

eg.如果n=2，则存在4个方格，其中，除一个方格外，其余三个方格可以被一个L型条块覆盖；当n=4时，则存在16个方格，其中，除一个方格外，其余15个方格被5个L型条块覆盖。

• （二）具体要求

输入一个正整数n，表示棋盘的大小时n*n的。输出一个被L型条块覆盖的n*n棋盘。

该棋盘除一个方格外，其余各方格都被L型条块覆盖住。为区别各个方格是被哪个L型条块所覆盖，每个L型条块用不同的数字、颜色或标记表示（这里我用的是不同数字表示）。

• （三）解题思路

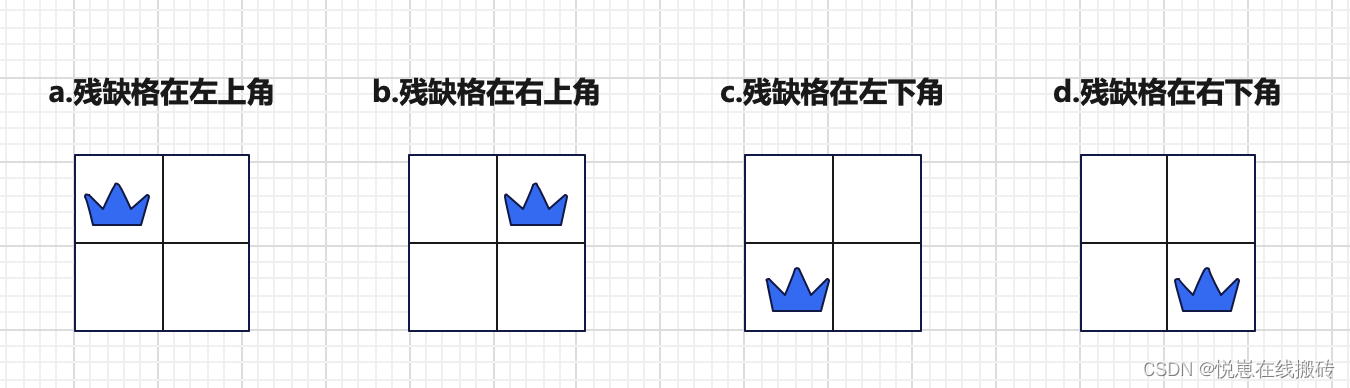
1.首先将问题分解，分成以下四种最基本的情况：

2.然后以较为复杂的4*4棋盘为例：

   此处假设残缺格在（1，2）位置，如图：