系列文章目录

第一章 【数据结构C++】线性表/顺序表-数组与vector
第二章 【数据结构C++】线性表/顺序表-数据类型、增删改查操作

前言

我们在第一章中认识了数据结构的内容，以及数组和Vector的语法和区别，这张我们着重学习数据结构中线性表的顺序存储结构的相关操作和应用。
最后给出通讯录的实现代码（下一期公布），将学到的知识融入项目中，加快理论和实践的融合，形成完整且牢固的知识体系结构。

一、线性表的顺序结构

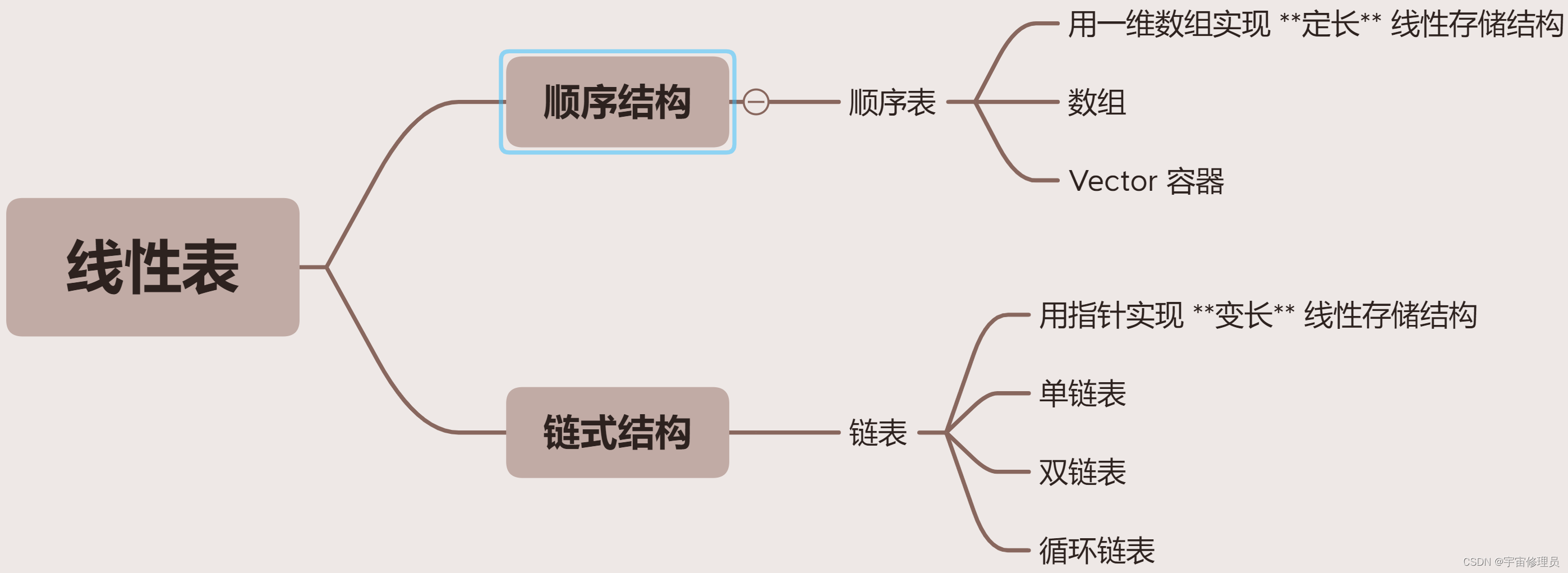
线性结构的特点：数据元素之间的逻辑关系是线性关系。
它的存储结构有两种：顺序结构、链式结构。而顺序表也分为：动态顺序表、静态顺序表。

1.1 第 i 个元素的地址计算方式

顺序表：用物理上的相邻（内存中的地址空间是线性的）实现数据元素之间的逻辑相邻关系。

假定线性表的每个元素占L个存储单元，若知道第一个元素的地址（基地址）为Loc(a0)，则位序为i的元素的地址为：Loc(a0)= Loc(a0)+i*L ，0≤i≤n-1。只要已知顺序表首地址 Loc(a0)和每个数据元素的大小L就可通过上述公式求出位序为i的元素的地址，时间复杂度为0(1)。

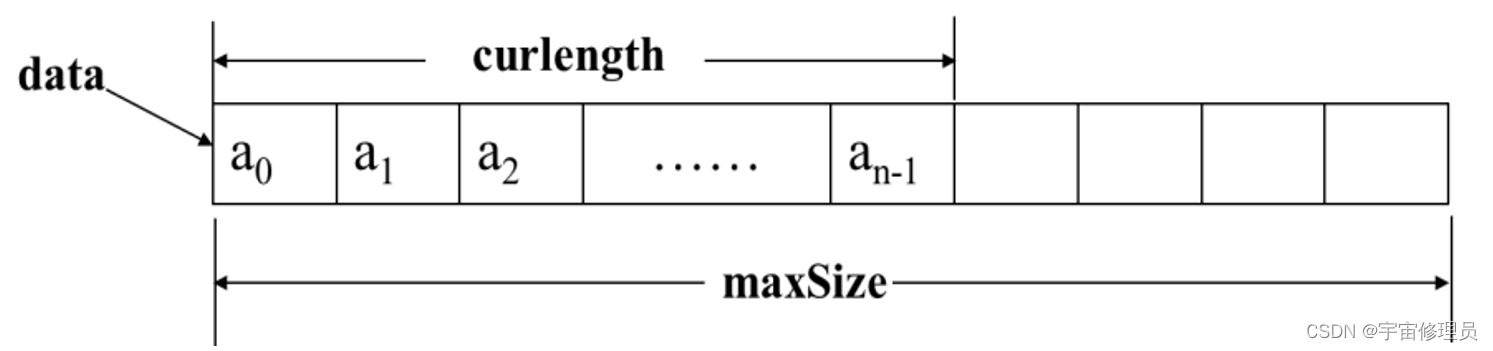
因此顺序表具有按数据元素的序号随机存取的特点，在C++语言中可用一维数组来实现定长的线性存储结构。若需要动态数组，需要三个变量：指向线性表元素类型的指针（data），数组规模(容量)，数组中的元素个数(表长)。

二、顺序表类型定义和功能函数-模板

template <class elemType>
class seqList{
	public List <elemType>{
		private:
			elemType *data;		//利用动态数组存储数据元素
			int curLength;		// 当前顺序表中存储的元素个数
			int maxSize;		//顺序表的最大长度
			void resize();		// 表满时扩大表空间
		
		public:
			seqList(int initSize =10);	//构造函数
			seqList(seqList & sl);		//拷贝构造函数
			~seqList(){delete []data;}  //析构函数
			
			void clear(){curLength=0;}  				// 清空表，只需置curLength为0
			
			bool empty()const{return curLength==0;}		// 判空
			
			int size()const{ return curLength;}			// 返回顺序表中当前存储元素的个数
			
			void traverse()const ;						// 遍历顺序表
			void insert(int i,const elemType &value);	// 逆置顺序表
			
			void inverse();								// 在位序i上插入值为value的元素
			void remove(int i);							// 删除位序i上的元素
			int search(const elemType &value)const ;	//查找值为value的元素第一次出现的位序
			elemType visit(int i) const;				// 访问位序为i的元素的值，“位序0”表示第一个元素

	}
}; 

2.函数的具体实现

2.1 构造函数:构造空顺序表

时间复杂度为O(1)，代码如下：

template <class elemType>
seqList<elemType>::seqList(int initSize=10){
	if(initSize <= 0) throw badSize();
	maxSize = initSize;
	data = new elemType[maxSize];
	curLength=0;
}

2.2 拷贝构造函数

在构造函数里动态分配了内存资源，这时需要用户自定义拷贝构造函数进行深拷贝，时间复杂度为O(N)，代码如下：

template <class elemType>
seqList<elemType>::seqList(seqList & sl){
	maxSize= sl.maxSize;
	curlength= sl. curlength;
	data = new elemType[maxSize];
	for(int i=0;i< curLength; ++i) 
		data[i]= sl.data[i];
}

2.3 遍历顺序表

时间复杂度为O(N)，代码如下：

template<class elemType>
void seqList<elemType>::traverse()const{
	if(empty()) cout<<"is empty"<<endl; //空表
	else{
		cout<<"output element:\n";
		for(int i=0;i< curLength;i++)// 依次访问顺序表中所有元素
		cout<<data i<<" ";cout<<endl;
	}
}

2.4 逆置顺序表

两两元素交换，共进行n/2次， 时间复杂度为O(N)，代码如下：

template<class elemType>
void seqList<elemType>::inverse(){
	elemType tmp;
	for(int i=0;i< curLength/2;i++){// 控制交换的次数
		tmp = data[i];
		data[i]= data[curLength-i-1];
		data[curLength-i-1]= tmp;
	}
}

2.5 求前驱和后继

时间复杂度为O(1)：线性表的顺序存储中，通过元素的下标可以直接定位其前驱和后继，有两种情况：

1. 若i == 0，则为第一个元素无前驱，否则其前驱是 data[i-1]；
2. 若i == curLength-1，则为最后一个元素无后继，否则其后继是 data[i+1]。

2.6 查找元素

两种常用方法：每个元素和待查找元素val进行比较 O(N)；二分查找 （适合有序且不含重复元素的序列数组）O(log N)，代码如下：

emplate<class elemType>
//暴力查找 
int seqList<elemType>::search(const elemType &value)const{
	for(int i=0;i< curLength;i++)
		if(value == data[i]) return i;
	
	return -1; //查找失败返回-1
}
//二分查找，适合有序且不含重复元素的序列数组
int seqList<elemType>::search(const elemType &value)const{
	int i=0,j=curLength-1；
	while(i<=j){
		//int mid=(i+j)/2;	会存在溢出现象
		int mid=i+(j-i)/2;				//mid=left+(right-left)/2
		if(data[mid]==value){
			return mid;
		}else if(data[mid]<value){
			i=mid+1;
		}else{
			j=mid-1;
		}
	} 
	return -1; //查找失败返回-1
} 

关于二分法int mid=(i+j)/2;溢出现象的解释，可以在这篇blog中学习到：
二分查找——mid=(left+right)/2溢出

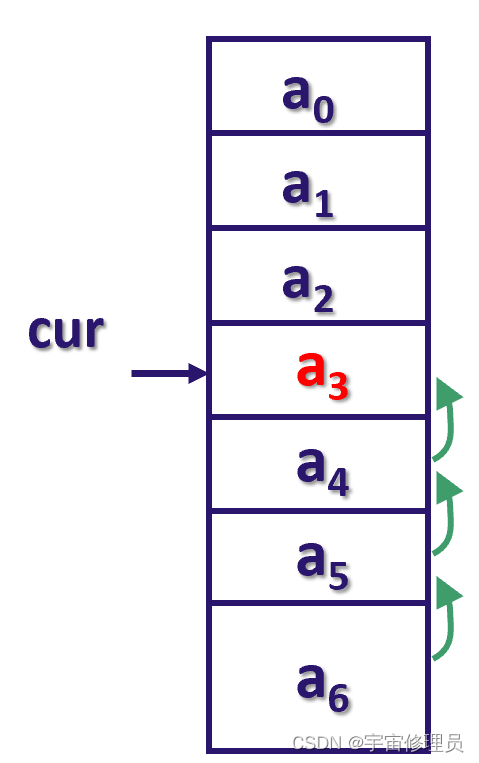
2.7 插入元素

时间复杂度为O(N)。

代码如下：

template <class elemType>
void seqList<elemType>::insert(int i, const elemType &value){
	if(i<0 || i>curLength) 
		throw outOfRange();		//合法的插入位置为[0..curLength]
	if(curLength==maxSize) 
		resize();				//表满，扩大
		
	//下标j-1在[curLength-1..i]范围的元素往后移动一步
	for (int j= curLength;j>i; --j) 	//最先移动表尾元素
		data[j]= data[j-1];
	
	data[i]= value;		//将 value 置入位序为i的位置
	++curLength;		//表的实际长度增1
}

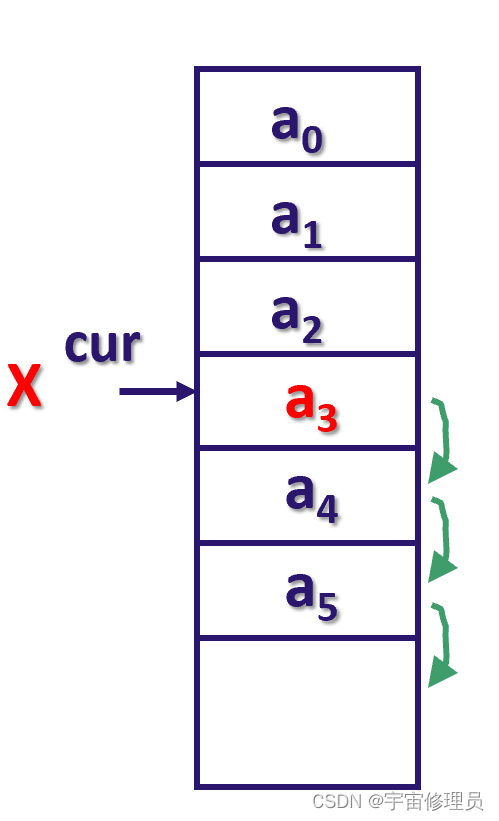
2.8 删除元素

顺序表中，元素只能覆盖，不能删除。 时间复杂度为O(N)。

template <class elemType>
void seqList<elemType>::remove(int i){
	//合法的删除位置为[0..curLength-1]
	if(i<0 || i> curLength-1)
		throw outOfRange();
	
	//[i+1..curLength-1]范围的元素往前移动一步
	for(int j=i;j< curLength-1;j++)
		data[j]= data[j+1];
		
	--curLength;	// 表的实际长度减 1
}

2.9 扩容

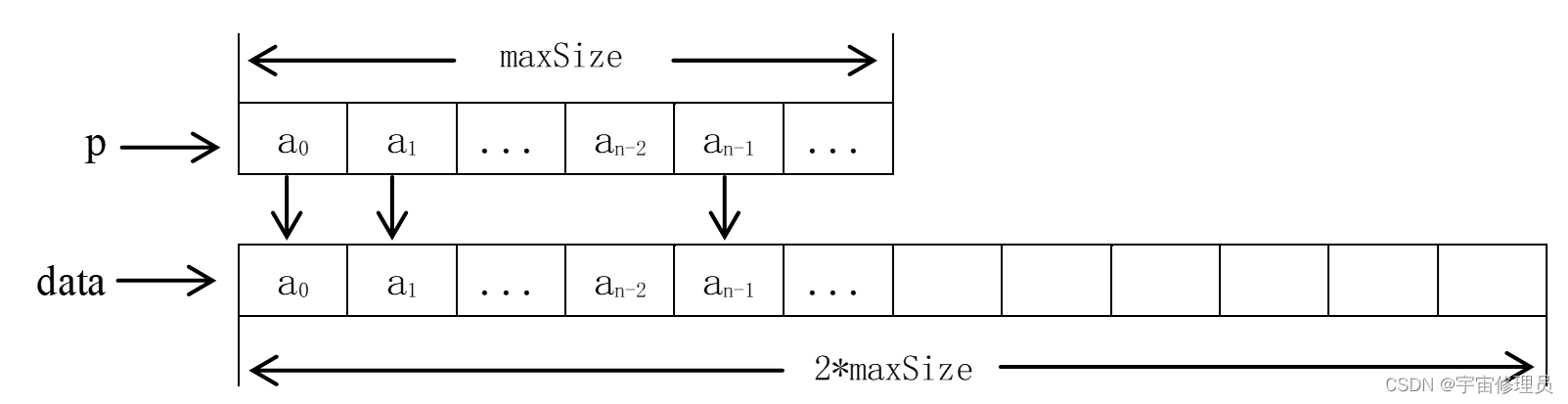
由于数组空间在内存中必须是连续的，因此，扩大数组空间的操作须重新申请一个更大规模的新数组，将原有数组的内容拷贝到新数组中，释放原有数组空间，将新数组作为线性表的存储区。时间复杂度为O(N)。

template <class elemType>
void seqList<elemType>::resize(){
	elemType *p= data;		// p指向原顺序表空间
	maxSize*=2;				// 表空间扩大2倍
	data = new elemType[maxSize];// data指向新的表空间
	
	for(int i=0;i< curLength; ++i)
		data[i]= p[i];		// 复制元素
	
	delete [] p; 
}

2.10合并顺序表

时间复杂度 O(m+n)

template<class elemType>
bool seqList<elemType>::Union(seqList<elemType> &B){
	int m, n, k, i, j;
	m= this->curLength;// 当前对象为线性表A
	n= B.curLength;//m，n分别为线性表A和B的长度
	k=m+n-1;//k为结果线性表的工作指针(下标)
	i= m-1.j= n-1;//i，j分别为线性表A和B的工作指针(下标)
	
	while(m+n > this->maxSize){// 判断A表空间是否足够大
		resize();// 空间不够，扩大表空间
	}
	
	while(i>=0 && j>=0){// 合并顺序表，直到一个表为空
		if(data[i]>= B.data[j]) data[k--]= data[i--];
		else data[k--]= B.data[j--];//默认当前对象
	}
	
	while(j>=0){// 将B表的剩余元素复制到A表
		data[k--]= B.data[j--];
		curLength= m+n;// 修改A表长度
	}
	
	return true;
}
 

总结

1. 预先分配存储空间： 顺序表需要预先分配存储空间，很难恰当预留空间分配大了造成浪费，分配小了对有些运算会造成溢出；
2. 随机存储： 由于逻辑次序和物理次序的一致性，顺序表能够按元素序号(下标)直接存取元素具有随机存取的优点；
3. 插入和删除效率低： 由于要保持逻辑次序和物理次序的一致性，顺序表在插入删除时需要移动大量的数据，因此顺序表的插入和删除效率低；
4. 创建新表： 改变顺序表的大小，需要重新创建一个新的顺序表把原表里的数据复制到新表，然后释放原表空间；
5. 顺序表比较适合静态的、经常做定位访问的线性表。