Leetcode(684)——冗余连接
题目
树可以看成是一个连通且 无环 的 无向 图。
给定往一棵 n 个节点 (节点值 1~n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间,且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ,edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。
请找出一条可以删去的边,删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案,则返回数组 edges 中最后出现的边。
示例 1:
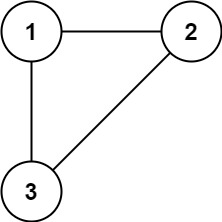
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]
示例 2:
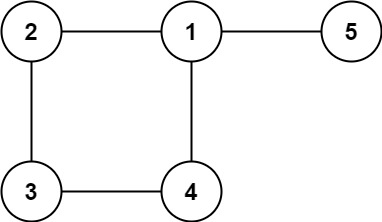
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
提示:
- n == edges.length
- 3 <= n <= 1000
- edges[i].length == 2
- 1 <= ai < bi <= edges.length
- ai != bi
- edges 中无重复元素
- 给定的图是连通的
题解
方法一:并查集
思路
因为在一棵树中,边的数量比节点的数量少
1
1
1。如果一棵树有
n
n
n 个节点,则这棵树有
n
−
1
n-1
n−1 条边。这道题中的图在树的基础上多了一条附加的边,因此边的数量也是
n
n
n。
树是一个连通且无环的无向图,在树中多了一条附加的边之后就会出现环,因此附加的边即为导致环出现的边。
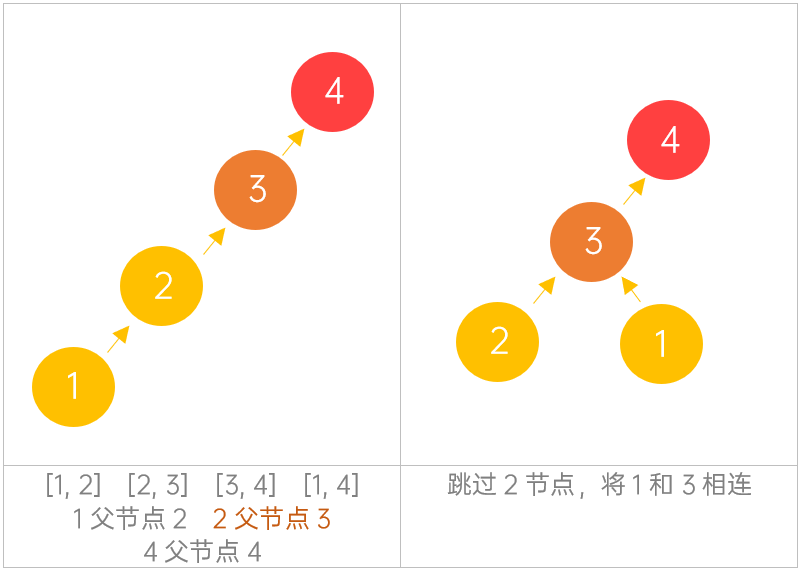
可以通过并查集寻找附加的边。初始时,每个节点都属于不同的连通分量。遍历每一条边,判断这条边连接的两个顶点是否属于相同的连通分量。
- 如果两个顶点属于不同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间不连通,因此当前的边不会导致环出现,合并这两个顶点的连通分量。
- 如果两个顶点属于相同的连通分量,则说明在遍历到当前的边之前,这两个顶点之间已经连通,因此当前的边导致环出现,为附加的边,将当前的边作为答案返回。
代码实现
我自己的:
class Solution {
int find(int node){ // 查找 node 的祖先
if(nodes[node] == node) return node;
else return find(nodes[node]);
}
vector<int> nodes; // 下标0不使用,数组长度为n+1
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
for(int n = 0; n < edges.size()+1; n++)
nodes.push_back(n); // 每个点对应的初始值都是它本身
vector<int> ans(2, 0);
int n0, n1;
for(auto &it: edges){
n0 = find(it[0]); // it[0] 所属树的祖先
n1 = find(it[1]); // it[1] 所属树的祖先
if(n0 != n1)
nodes[n0] = nodes[n1]; // 合并两个集合
else{
ans[0] = it[0];
ans[1] = it[1];
break;
}
}
return ans;
}
};
Leetcode 官方题解:
class Solution {
public:
int Find(vector<int>& parent, int index) {
if (parent[index] != index) {
parent[index] = Find(parent, parent[index]);
}
return parent[index];
}
void Union(vector<int>& parent, int index1, int index2) {
parent[Find(parent, index1)] = Find(parent, index2);
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
vector<int> parent(n + 1);
for (int i = 1; i <= n; ++i) {
parent[i] = i;
}
for (auto& edge: edges) {
int node1 = edge[0], node2 = edge[1];
if (Find(parent, node1) != Find(parent, node2)) {
Union(parent, node1, node2);
} else {
return edge;
}
}
return vector<int>{};
}
};
复杂度分析
时间复杂度:
O
(
n
l
o
g
n
)
O(nlogn)
O(nlogn),其中
n
n
n 是图中的节点个数。需要遍历图中的
n
n
n 条边,对于每条边,需要对两个节点查找祖先,如果两个节点的祖先不同则需要进行合并,需要进行
2
2
2 次查找和最多
1
1
1 次合并。一共需要进行
2
n
2n
2n 次查找和最多
n
n
n 次合并,因此总时间复杂度是
O
(
2
n
log
n
)
=
O
(
n
log
n
)
O(2n \log n)=O(n \log n)
O(2nlogn)=O(nlogn)。这里的并查集使用了路径压缩,但是没有使用按秩合并,最坏情况下的时间复杂度是
O
(
n
log
n
)
O(n \log n)
O(nlogn),平均情况下的时间复杂度依然是
O
(
n
α
(
n
)
)
O(n \alpha (n))
O(nα(n)),其中
α
\alpha
α 为阿克曼函数的反函数,
α
(
n
)
\alpha (n)
α(n) 可以认为是一个很小的常数。
空间复杂度:
O
(
n
+
m
)
O(n+m)
O(n+m),其中
n
n
n 是图中的节点个数,
m
m
m 是递归层数。使用数组
nodes
\textit{nodes}
nodes 记录每个节点的祖先。
方法二:并查集 + 路径压缩
思路
并查集与上面一致,只是在查找函数中使用了压缩路径的技巧,从而使得下次的查找更快。
代码实现
我自己的:
class Solution {
// 采用路径压缩,使得下次查找更快-------------------------------
int find(int node){ // 查找 node 的祖先
if(nodes[node] == node) return node;
else return nodes[node] = find(nodes[node]);
}
vector<int> nodes; // 下标0不使用,数组长度为n+1
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
for(int n = 0; n < edges.size()+1; n++)
nodes.push_back(n); // 每个点对应的初始值都是它本身
vector<int> ans(2, 0);
int n0, n1;
for(auto &it: edges){
n0 = find(it[0]); // it[0] 所属树的祖先
n1 = find(it[1]); // it[1] 所属树的祖先
if(n0 != n1)
nodes[n0] = nodes[n1]; // 合并两个集合
else{
ans[0] = it[0];
ans[1] = it[1];
break;
}
}
return ans;
}
};
复杂度分析
时间复杂度:
O
(
n
log
n
)
O(n \log n)
O(nlogn),其中
n
n
n 是图中的节点个数。需要遍历图中的
n
n
n 条边,对于每条边,需要对两个节点查找祖先,如果两个节点的祖先不同则需要进行合并,需要进行
2
2
2 次查找和最多
1
1
1 次合并。一共需要进行
2
n
2n
2n 次查找和最多
n
n
n 次合并,因此总时间复杂度是
O
(
2
n
log
n
)
=
O
(
n
log
n
)
O(2n \log n)=O(n \log n)
O(2nlogn)=O(nlogn)。这里的并查集使用了路径压缩,但是没有使用按秩合并,最坏情况下的时间复杂度是
O
(
n
log
n
)
O(n \log n)
O(nlogn),平均情况下的时间复杂度依然是
O
(
n
α
(
n
)
)
O(n \alpha (n))
O(nα(n)),其中
α
\alpha
α 为阿克曼函数的反函数,
α
(
n
)
\alpha (n)
α(n) 可以认为是一个很小的常数。
空间复杂度:
O
(
n
)
O(n)
O(n),其中
n
n
n 是图中的节点个数。使用数组
parent
\textit{parent}
parent 记录每个节点的祖先。