💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
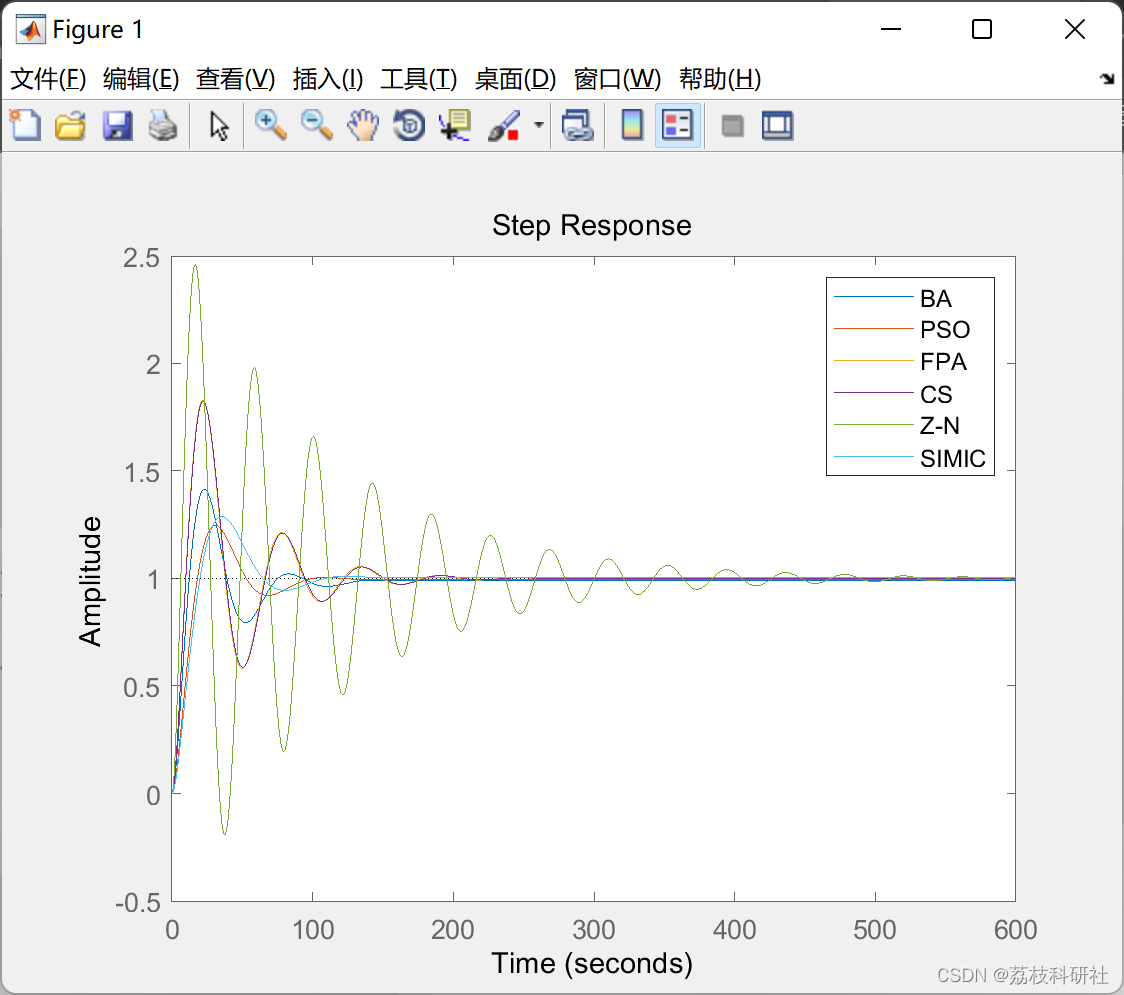
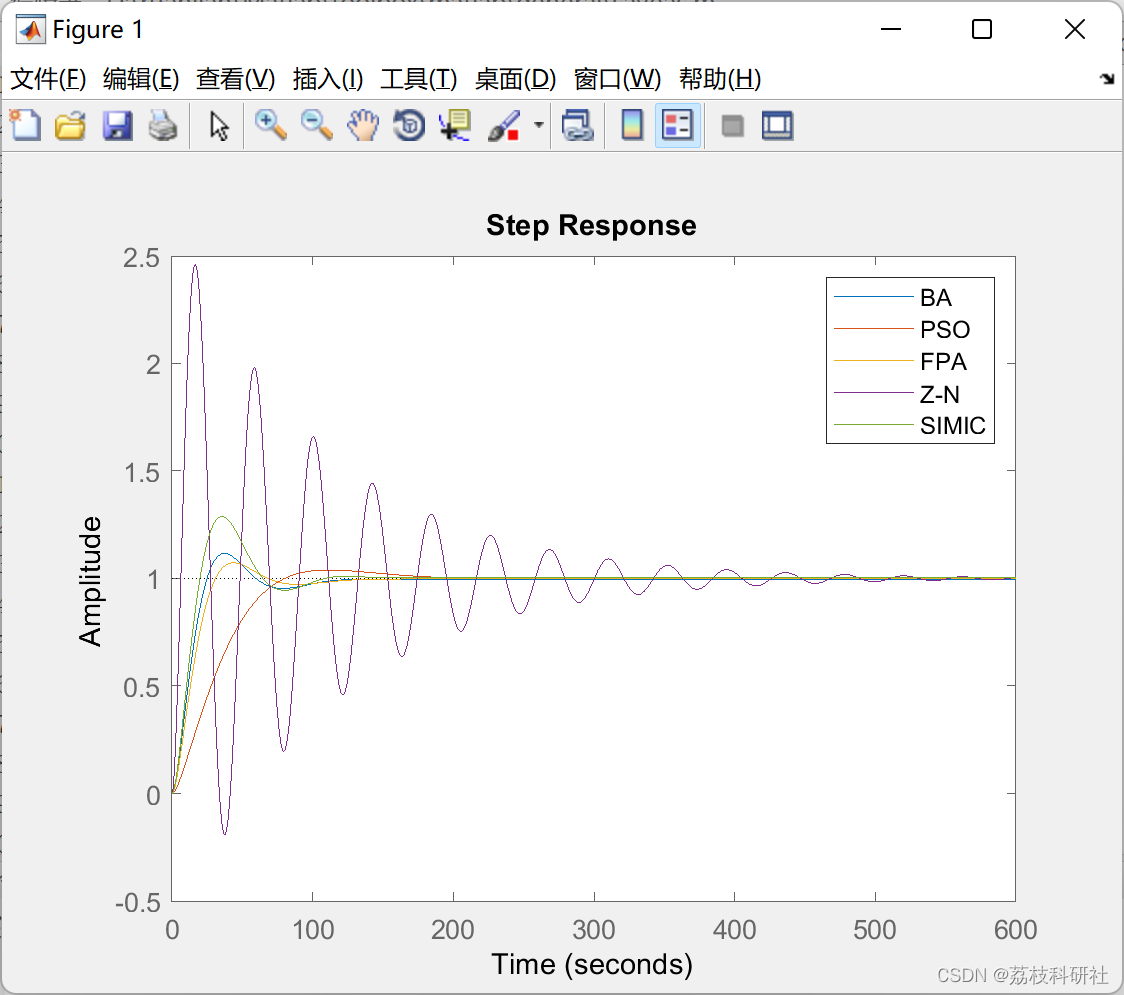
本文采用蝙蝠算法、粒子群优化、花轮询算法和布谷鸟搜索算法,对管壳式换热器的控制系统进行了建模和计算机仿真。为了评估不同调整方法的性能,本文比较了生成的八个网格设置中的阶跃响应瞬态值。它还使用文献中提出的性能指标对这两种类型的网格进行了比较,通过蝙蝠算法优化的系统获得了与粒子群优化、布谷鸟搜索算法和花朵轮询算法相关的最佳瞬时值。性能指标FPA和PSO获得了较好的结果。
将这些算法应用于换热器PI控制器的优化是一个复杂而有趣的问题。换热器的性能直接影响到工业生产中能源利用的效率和成本。让我来帮你梳理一下这个问题,然后我们可以逐步思考如何将这些算法结合起来进行优化。
-
启发式蝙蝠算法(Bat Algorithm, BA):蝙蝠算法灵感来源于蝙蝠的回声定位行为,是一种全局优化算法。在换热器PI控制器的优化中,BA可以用于自动调整控制器的比例(P)和积分(I)参数,以达到系统的最优控制性能,如快速响应、稳定性和最小误差。通过不断迭代更新参数,并根据蝙蝠飞行的模拟规则(包括频率变化、声音强度衰减等),BA能够在多维参数空间中寻找最佳的控制器设置。
-
粒子群优化算法(Particle Swarm Optimization, PSO):PSO模仿鸟群的集体行为,每个粒子代表一个潜在解,在搜索空间中通过不断更新其位置和速度来探索最优解。应用到换热器PI控制器优化上,可以通过初始化一群代表不同PI参数组合的粒子,然后根据历史最优解和个人最优解调整每个粒子的位置,从而逐步接近最优的控制器参数配置,提高系统控制效果。
-
花轮询算法(Flower Pollination Algorithm, FPA):这是一种受自然界中花粉传播过程启发的全局优化算法。FPA通过模拟两种花粉传播机制(自花粉传播和异花粉传播)来搜索解空间,适用于解决复杂的优化问题。在换热器PI控制器参数优化场景下,FPA可以促进搜索过程中的多样性保持和局部精细搜索的平衡,有助于发现更广泛且高质量的控制器参数配置。
-
布谷鸟搜索算法(Cuckoo Search Algorithm, CSA):CSA模拟了布谷鸟的繁殖行为以及其对寄主巢穴的利用策略,结合了Levy飞行策略以实现高效的全局搜索。应用于换热器PI控制器优化,CSA能够高效地探索参数空间,通过不断生成新的解决方案(如同布谷鸟产卵)并根据适应度评价保留或抛弃(如同寄主鸟的巢穴选择机制),从而找到使控制系统性能最优的PI参数组合。
结合这些智能算法,研究者可以综合考虑算法的收敛速度、搜索能力和适用性,设计混合或改进算法来提升换热器PI控制器的优化效果。例如,可以通过算法融合或引入自适应机制,根据优化过程中的信息反馈动态调整算法参数,以更好地应对换热器控制过程中的非线性、时变性等问题,实现更加精准和高效的控制目标。这样的研究不仅能推动换热器控制技术的进步,也为其他工业控制领域提供有益的方法论参考。
在实际应用中,需要根据具体的换热器系统和优化目标来选择合适的算法组合,并进行参数调节和优化策略的设计。
📚2 运行结果
部分代码:
% Draw n Levy flight sample
function L = Levy(d)
% Levy exponent and coefficient
% For details, see Chapter 11 of the following book:
% Xin-She Yang, Nature-Inspired Optimization Algorithms, Elsevier, (2014).
beta=3/2;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
u=randn(1,d)*sigma;
v=randn(1,d);
step=u./abs(v).^(1/beta);
L=0.01*step;
end
%% --------------- All subfunctions are list below ------------------
%% Get cuckoos by ramdom walk
function nest=get_cuckoos(nest,best,Lb,Ub)
% Levy flights
n=size(nest,1);
% Levy exponent and coefficient
% For details, see equation (2.21), Page 16 (chapter 2) of the book
% X. S. Yang, Nature-Inspired Metaheuristic Algorithms, 2nd Edition, Luniver Press, (2010).
beta=3/2;
sigma=(gamma(1+beta)*sin(pi*beta/2)/(gamma((1+beta)/2)*beta*2^((beta-1)/2)))^(1/beta);
for j=1:n,
s=nest(j,:);
% This is a simple way of implementing Levy flights
% For standard random walks, use step=1;
%% Levy flights by Mantegna's algorithm
u=randn(size(s))*sigma;
v=randn(size(s));
step=u./abs(v).^(1/beta);
% In the next equation, the difference factor (s-best) means that
% when the solution is the best solution, it remains unchanged.
stepsize=0.01*step.*(s-best);
% Here the factor 0.01 comes from the fact that L/100 should the typical
% step size of walks/flights where L is the typical lenghtscale;
% otherwise, Levy flights may become too aggresive/efficient,
% which makes new solutions (even) jump out side of the design domain
% (and thus wasting evaluations).
% Now the actual random walks or flights
s=s+stepsize.*randn(size(s));
% Apply simple bounds/limits
nest(j,:)=simplebounds(s,Lb,Ub);
end
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。