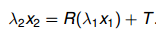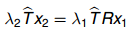1. 间接法进行运动恢复的前提假设
对于结构与运动或视觉三维重建中,通常假设已经通过特征匹配等方法获取了匹配好的点对。
先求出匹配点对再获取结构和运动信息的方法称作间接法。
间接法最重要的三个假设是:
1.拥有一系列两帧之间的匹配点对。但同时假设匹配关系不一定精确:
- 匹配点不一定精确,即对于匹配点对 ( A n , A n + 1 ) (A_n,A_{n+1}) (An,An+1), A n + 1 A_{n+1} An+1可能并非 A n A_n An的真实匹配 点,而是在它周围;
- 匹配关系不一定正确。
2.场景是静态的,即环境中不存在运动的物体
3.知道相机内参数且内参数恒定不变
此处的匹配点,可以是2D-2D(单目相机初始化时),2D-3D配对点(单目相机运行过程中,已经算出了3D的地图点,又来了2D的图形),或是3D-3D的匹配点(使用双目相机、RGBD相机或其他传感器,可以直接过间接获取匹配好的三维点对)。本文讨论的主要是是基于2D-2D的配对点。
2.极线约束,本征矩阵
2.1 极线约束:
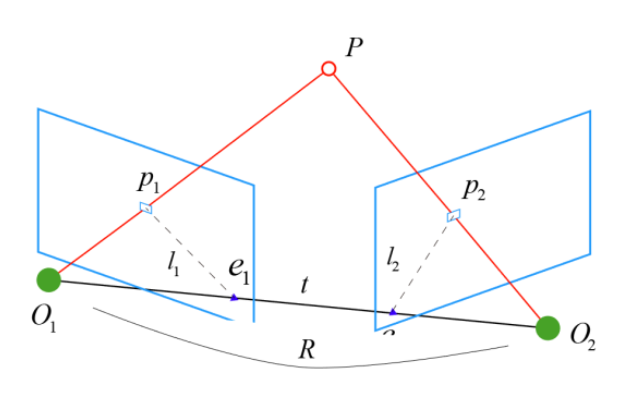
物理世界上的一个三维点P投影到两个成像面(实际上像面也常常处理成z=1的地方)上,点P与两个像面的光心形成一个对极平面, l 1 , l 2 l_1,l_2 l1,l2分别为对极平面与像平面相交的极线。
极线约束是指对第一个成像面上的点p1,它在第二个平面上的对应点p2总存在于对应的极线 l 2 l_2 l2上。
用 x x x表示像平面坐标的话, K K K为内参数矩阵,P为相机坐标系三维点;如果已知内参数 K K K,则可以去掉 K K K的影响,即令 x = K − 1 p x = K^{-1}p x=K−1p,得到
λ 1 x 1 = P , λ 2 x 2 = R P + T \lambda_1x_1 = P,\lambda_2x_2 = RP+T λ1x1=P,λ2x2=RP+T
即:
λ 2 x 2 = λ 1 R x 1 + T \lambda_2 x_2 = \lambda_1Rx_1+T λ2x2=λ1Rx1+T(2-1)
此处的 x 1 , x 2 x_1,x_2 x1,x2可以看做是 z = 1 z=1 z=1平面上的点。
2.1.1 极线约束(Epipolar constraint,essential constraint,bilinear constraint):
对于两帧之间的归一化坐标 x 1 , x 2 x_1,x_2 x1,x2,
x 2 T T ^ R x 1 = 0 , ( 2 − 1 ) x_2^T\hat TRx_1 = 0,(2-1) x2TT^Rx1=0,(2−1)
其推导过程如下:
1。由于 λ x = X \lambda x = X λx=X(相机坐标系下世界坐标),则可得:
R,T分别为旋转和平移矩阵。
2.左右分别左乘 T ^ \hat T T^,即得到
3.左乘 x 2 x_2 x2,除掉 λ \lambda λ影响:(将此缩放因子放入E中,此缩放因子在4部分会介绍),将上式左右两边投影到 x 2 x_2 x2上,即左乘上 x 2 T x_2^T x2T,左侧即为0(因为 T × x 2 垂 直 于 x 2 , 因 此 左 乘 x 2 即 为 0 T\times x_2垂直于x_2,因此左乘x_2即为0 T×x2垂直于x2,因此左乘x2即为0),得极线约束:
x 2 T T ^ R x 1 = 0 x_2^T\hat T Rx_1 = 0 x2TT^Rx1=0
注:
上述2,3过程中, T ^ , x 2 \hat T,x_2