👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆下载资源链接👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆👆
《《《《《《《《更多资源还请持续关注本专栏》》》》》》》
论文与完整源程序_电网论文源程序的博客-CSDN博客
https://blog.csdn.net/LIANG674027206?type=download摘要--受导航和跟踪应用程序的推动在传感器网络中，我们考虑的问题是执行K Alman滤波与间歇观测。当数据传输时沿着不可靠的通信通道在大型、无线、多跳传感器网络，通信时延的影响和控制回路中的信息丢失不能被忽略。我们从离散卡尔曼滤波入手解决这一问题公式，并将观测的到达建模为随机过程。我们研究了统计收敛性质。的估计误差协方差，表明存在一个观测到达率的临界值，超出这意味着向无界状态错误的转变发生协方差。我们还给出了预期状态误差的上界和下界协方差。
部分代码展示：
%20synchronization/% Kalman Filtering With Intermittent Observations(2004)
close all
clear
clc
A=[1.25 1 0;0 0.9 7;0 0 0.6];C=[1 0 2];Q=20*eye(3,3);R=2.5; % 参数设置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
lambdadown=1-1/(max(eig(A)))^2; %下界
lambda=0:0.002:1; %设置步长（控制好精度，涉及上界的精度）（太大影响精度；太小影响效率）
Trs=1e5*ones(size(lambda)); %设成无穷大
k=1;
for i=lambda
A1=A*sqrt(1-i);
if i>lambdadown
s=dlyap(A1,Q);
Trs(k)=trace(s);
end
k=k+1;
end
plot(lambda,Trs,'-.r')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
n=length(lambda); %上界
T=zeros(n,1);
for i=1:n
setlmis([]);
Y=lmivar(1,[3,1]); %与矩阵A同阶的对称矩阵
Z=lmivar(2,[3,1]); %矩阵Z的行数与矩阵A行数相等，列与矩阵C的行数相等
lmiterm([-1 1 1 Y],1,1);
lmiterm([-1 1 2 Y],sqrt(lambda(i)),A);
lmiterm([-1 1 2 Z],1,C);
lmiterm([-1 1 3 Y],sqrt(1-lambda(i)),A);
lmiterm([-1 2 2 Y],1,1);
lmiterm([-1 3 3 Y],1,1);
lmiterm([-2 1 1 Y],1,1);
lmiterm([-3 1 1 0],1);
lmiterm([3,1 1,Y],1,1);
lmisys=getlmis;
options=[0 0 0 0 1];
[t,xopt]=feasp(lmisys,options);
T(i)=t;
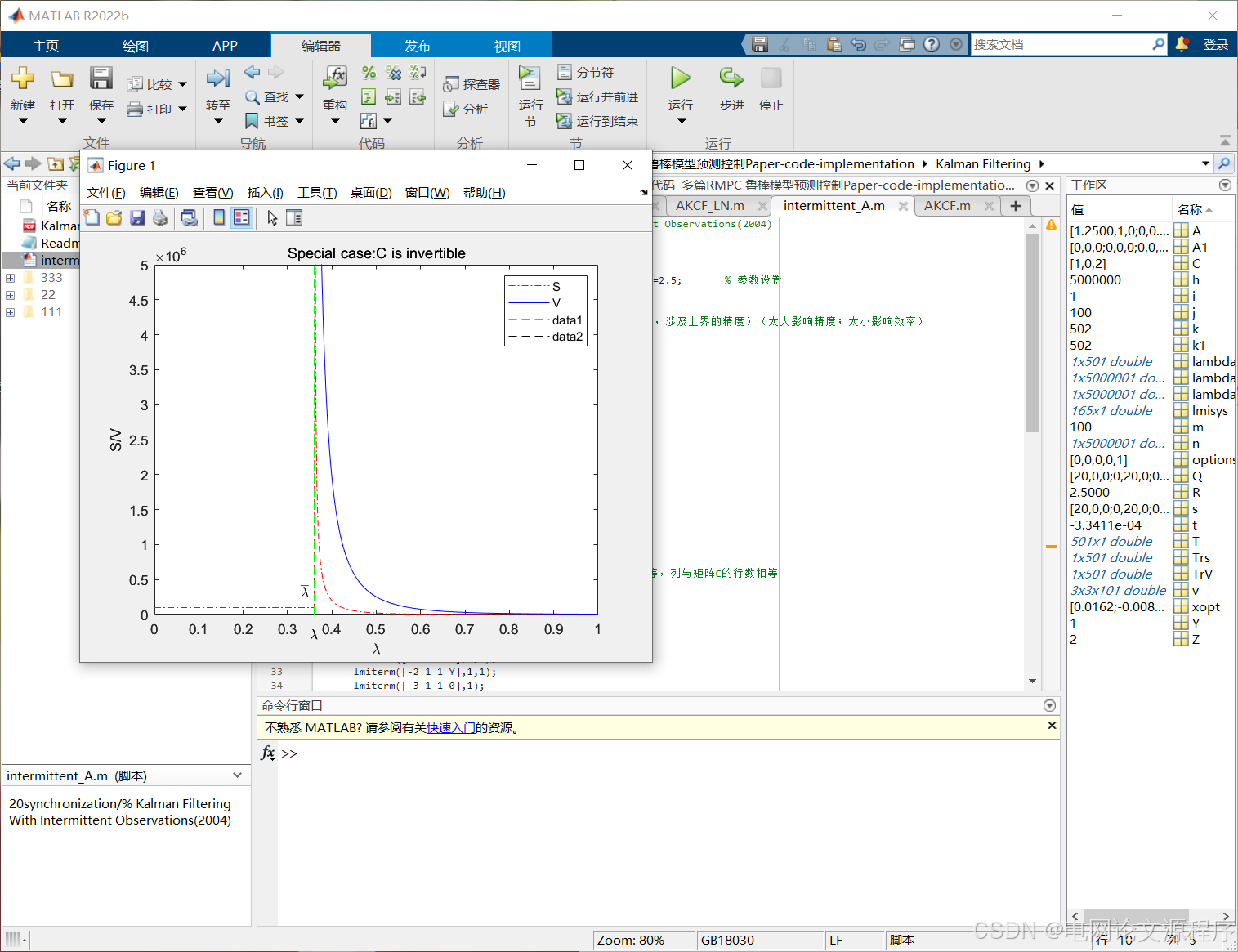
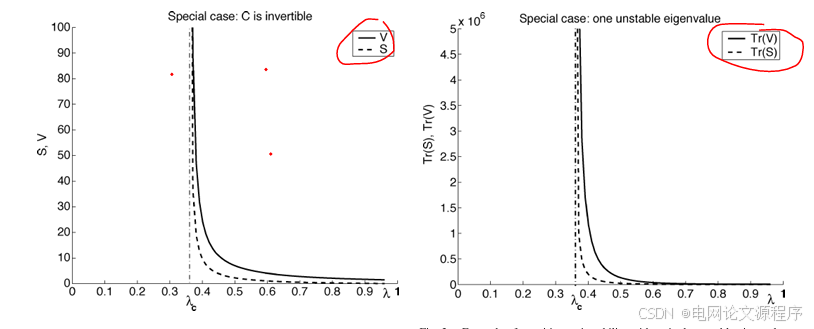
end效果展示：
202号资源-源程序：（SCI论文+程序）间歇观测的卡尔曼滤波-本人博客有解读资源-CSDN文库
《《《《《《《《更多资源还请持续关注本专栏》》》》》》》
论文与完整源程序_电网论文源程序的博客-CSDN博客