Bootstrap

14.代码随想录算法训练营第十四天|226. 翻转二叉树 ，101.对称二叉树 ，104. 二叉树的最大深度，111.二叉树的最小深度，[自学打卡记录]

14.代码随想录算法训练营第十四天|226. 翻转二叉树 - 力扣（LeetCode），101.对称二叉树 （优先掌握递归），104. 二叉树的最大深度 - 力扣（LeetCode），111.二叉树的最小深度，[自学打卡记录]

226. 翻转二叉树 - 力扣（LeetCode）

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

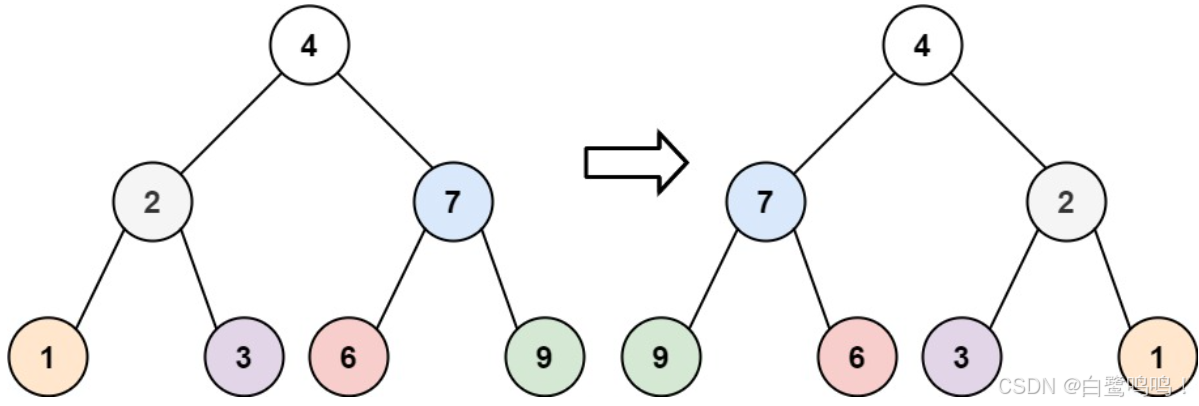
在这里插入图片描述

输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

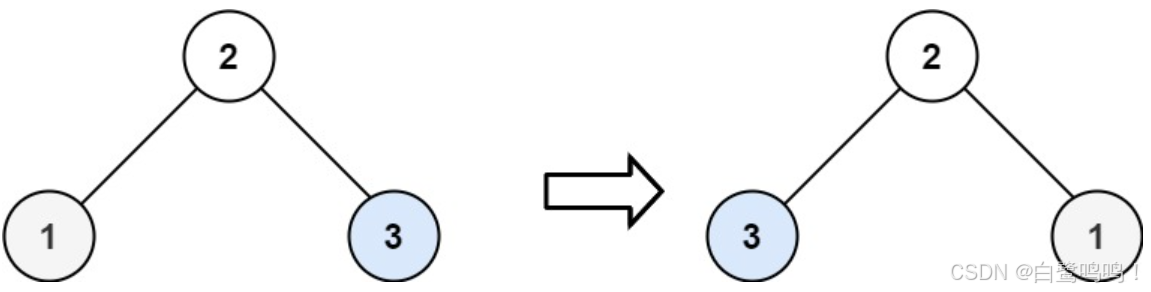
在这里插入图片描述

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

  • 树中节点数目范围在 [0, 100] 内
  • -100 <= Node.val <= 100

思想：无论哪一种遍历方式，只有遍历到的节点充当根节点的时候才能够进行处理。

解法一前序遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        swap(root);
        invertTree(root.left);
        invertTree(root.right);

        return root;
    }

    private void swap(TreeNode root){
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

解法二后序遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        
        invertTree(root.left);
        invertTree(root.right);
        swap(root);
        return root;
    }

    private void swap(TreeNode root){
        TreeNode tmp = root.left;
        root.left = root.right;
        root.right = tmp;
    }
}

解法三层次遍历：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if(root == null){
            return null;
        }
        ArrayDeque<TreeNode> deque = new ArrayDeque<>();
        deque.offer(root);
        while(!deque.isEmpty()){
            int size = deque.size();
            while(size-- > 0){
                TreeNode node = deque.poll();
                swap(node);
                if(node.left != null){
                    deque.offer(node.left);
                }
                if(node.right != null){
                    deque.offer(node.right);
                }
            }
        }
        return root;
    }
    public void swap(TreeNode node){
        TreeNode temp = node.left;
        node.left = node.right;
        node.right = temp;
    }
}

101. 对称二叉树 - 力扣（LeetCode）

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

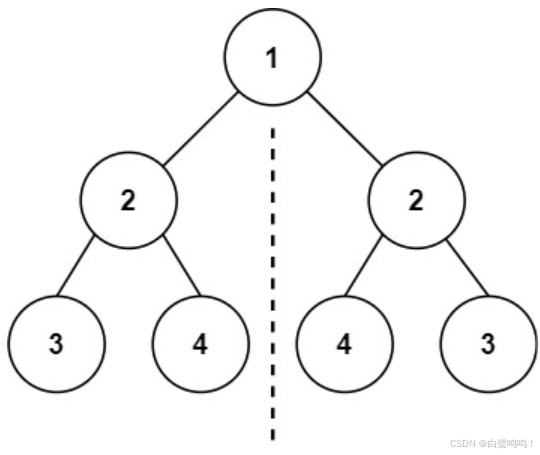
在这里插入图片描述

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

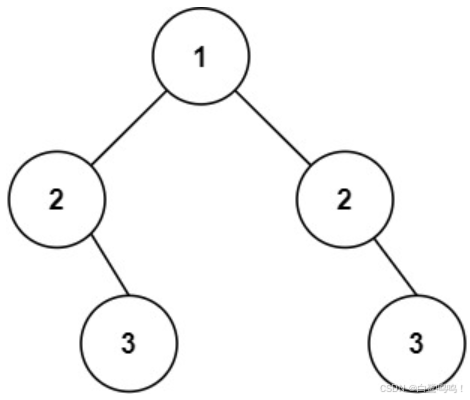
在这里插入图片描述

输入：root = [1,2,2,null,3,null,3]
输出：false

思想：需要收集孩子信息的话就需要用后序算法。（递归法）

  • 判断递归函数的参数，因为要比较的是左右两棵子树，所以参数是左子树节点和右子树节点；
  • 确定终止条件：
    • 左节点为空，右节点不为空，不对称
    • 左不空，右空，不对称
    • 左右空，对称
    • 左右都不为空，节点值不相同就return false
    • 左右都不为空，节点值相同：
      • 继续处理
  • 继续处理：
    • 比较外侧节点，左子树的左孩子，右子树的右孩子
    • 比较内侧节点，左子树的有孩子，右子树的左孩子
    • 如果左右都对称就返回true，有一侧不对称就返回false
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null){
            return true;
        }
        return compare(root.left,root.right);
    }

    boolean compare(TreeNode left,TreeNode right){
        if(left!=null && right==null){
            return false;
        }else if(left==null && right!=null){
            return false;
        }else if(left==null && right==null){
            return true;
        }else if(left.val != right.val){
            return false;
        }else{
            boolean inside = compare(left.right,right.left);
            boolean outside = compare(left.left,right.right);
            return inside && outside;
        }
    }
}

104. 二叉树的最大深度 - 力扣（LeetCode）

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

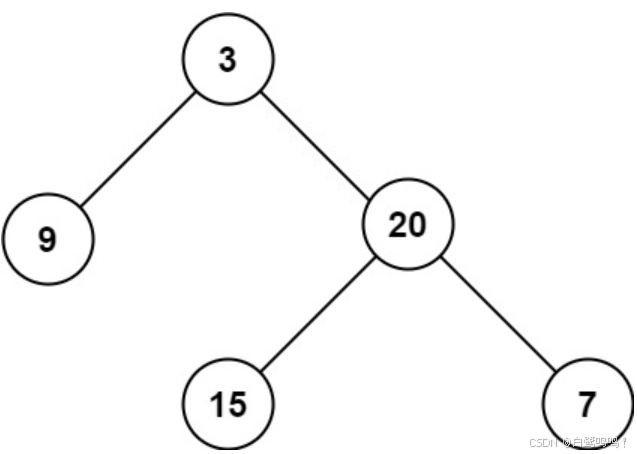
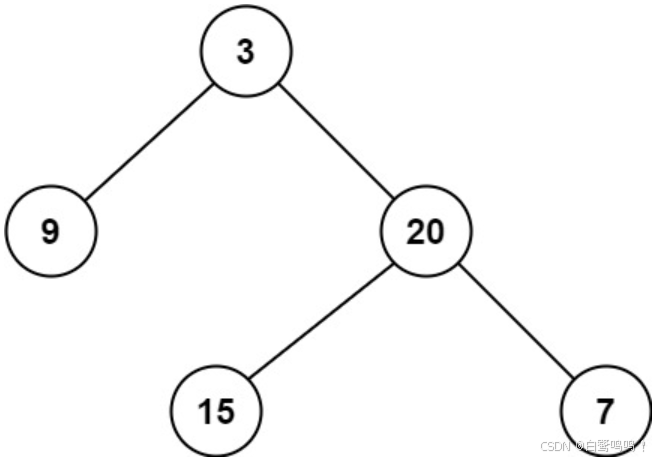
在这里插入图片描述

输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：

输入：root = [1,null,2]
输出：2

提示：

  • 树中节点的数量在 [0, 104] 区间内。
  • -100 <= Node.val <= 100

思想：根节点的高度就是我们这棵树的最大深度

  • 返回值是int
  • 参数是根节点
  • 终止条件：node==null return 0；
  • 用后序遍历
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftHight = maxDepth(root.left);
        int rightHight = maxDepth(root.right);
        return Math.max(leftHight,rightHight)+1;
    }
}

111. 二叉树的最小深度 - 力扣（LeetCode）

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

**说明：**叶子节点是指没有子节点的节点。

示例 1：

在这里插入图片描述

输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

  • 树中节点数的范围在 [0, 105] 内
  • -1000 <= Node.val <= 1000

思想：请根节点的最小高度

  • 终止条件 if(node == null) return 0；
  • 取左右子树的高度
  • 为什么不能return min（left，right）—和最大深度的区别
    • 因为这种把左子树为空，右子树不为空的情况考虑进去了（这个时候应该只考虑右子树的最小高度）
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int minDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int leftDepth = minDepth(root.left);
        int rightDepth = minDepth(root.right);

        if(root.left == null && root.right != null){
            return rightDepth+1;
        }
        
        if(root.left != null && root.right == null){
            return leftDepth+1;
        }

        return Math.min(leftDepth,rightDepth)+1;
    }
}

悦读

道可道，非常道；名可名，非常名。 无名，天地之始，有名，万物之母。 故常无欲，以观其妙，常有欲，以观其徼。 此两者，同出而异名，同谓之玄，玄之又玄，众妙之门。

最新收录
几款优秀的国内wordpress主题和其作者网站推荐
IO零拷贝技术
Chrome无法使用Unity Web Player的解决方案
傅里叶变换（FFT）理论与算法实现
UE几种异步加载
从0开始搭建SQL Server AlwaysOn 第三篇（配置AlwaysOn）
【接口测试笔记】postman+newman实现接口集合一键执行
SM2&SM3&SM4 Java实现分析
看哨兵快速理解快速排序算法
Win10家庭版升级Win11系统全攻略
;