前言
傅立叶变换是近代数值数学最重要的成果之一 , 在众多领域中发挥了很大的作用 , 它的意文远远超过一个算法 的范围 , 它使某些数据的事后处理及系统的模拟研究进入到数据的实时处理 , 傅立叶变换是信号分析和处理的有力工具 , 在数字信号处理和图像处理等方面为广泛采用数字方法打开一个崭新 的局面 。 在快速傅立叶变换算法为代表 的 一系列有效算法出现后 , 傅立叶变换不但在信号处理领域起着支柱作用 , 而且在其它工程领域也 获得了广泛的应用 。
在数字信号处理的领域,DFT 是对信号进行处理的一种重要的手段,并且广泛应用,实现了以频率为变量对信号和系统进行处理。其变换的概念可以理解为将时域信号分解成频率若干个不同的正弦或者余弦信号,亦可类比为光通过棱镜的分解作用。通过傅里叶变换,可以将信号转到频域内进行处理,为信号处理提供了更多可能。但是直接进行 DFT 运算的运算量与 DFT 序列的长度的平方成正比,可想而知,当序列很长时,计算量会让傅里叶变换难以实现。因此,为了简化运算,人们提出了快速傅里叶变换,大大减少了 DFT 运算量。
1、离散傅里叶变换(DFT)
2、快速傅里叶变换(FFT)
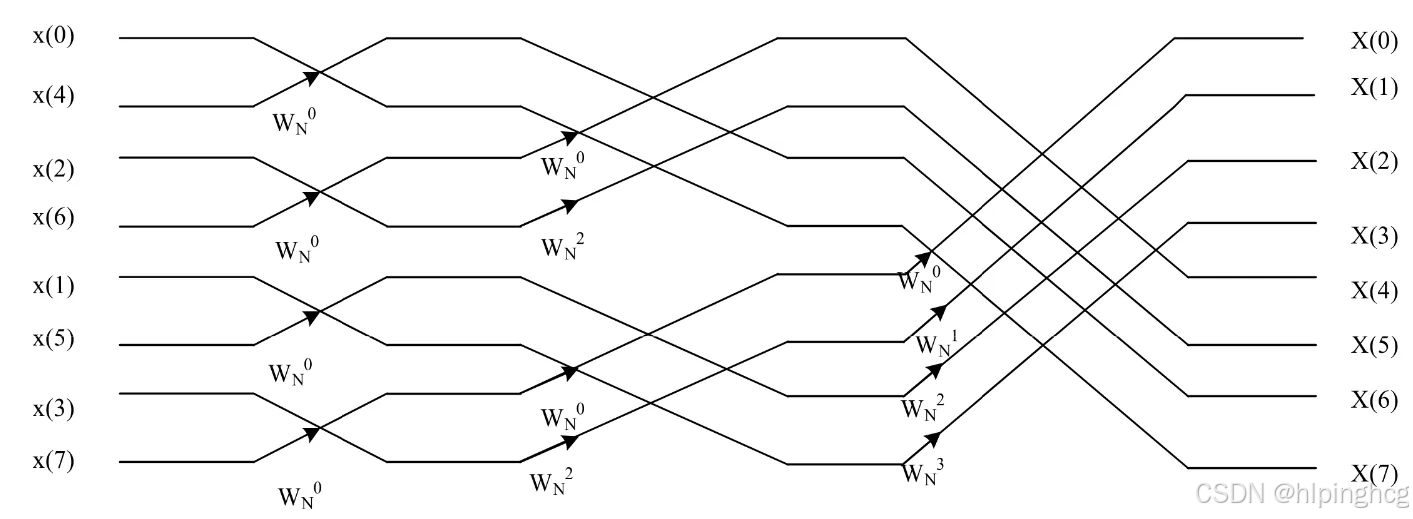
2.1 基-2FFT 算法
3、算法实现
3.1 C语言实现
#include "stdio.h"
/* Defines -------------------------------------------------------------------*/
#define q 10 // 采样点数 2^q
#define N (1<<q) // 2^q 点数
#define Fs 10000 // 采样率 Fs > 2fh
//typedef float real;
typedef struct {
float Re;
float Im;
} complex;
/* Typedefs -------------------------------------------------------------------*/
void fft(complex *v, int n, complex *tmp) ;
void Asm_Mag(complex *x, int n);
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#include "fft.h"
/* Private Defines ---------------------------------------------------------*/
// 计算幅值并打印
void Asm_Mag(complex *x, int n) {
int i;
float Mag;
float MagBuf[n/2];
for (i = 0; i < n / 2; i++) {
Mag = sqrt(x[i].Re * x[i].Re + x[i].Im * x[i].Im) * 2 / N; // 正频率分量乘以2
if (i == 0) {
Mag = Mag / 2; // 直流分量不需要乘以2
}
//printf("第%d个点:%.3f hz 幅度:%.3f \n", i, (float)i * Fs / N, Mag);
printf("频率,幅值:%.3f,%.3f\n", (float)i * Fs / n, Mag);
}
}
// 递归FFT实现
void fft(complex *v, int n, complex *tmp) {
if (n > 1) {
int k, m;
complex z, w, *vo, *ve;
ve = tmp;
vo = tmp + n / 2;
for (k = 0; k < n / 2; k++) {
ve[k] = v[2 * k];
vo[k] = v[2 * k + 1];
}
fft(ve, n / 2, v); // FFT 偶序列
fft(vo, n / 2, v); // FFT 奇序列
for (m = 0; m < n / 2; m++) {
w.Re = cos(2 * 3.1415926f * m / (float)n);
w.Im = -sin(2 * 3.1415926f * m / (float)n);
z.Re = w.Re * vo[m].Re - w.Im * vo[m].Im;
z.Im = w.Re * vo[m].Im + w.Im * vo[m].Re;
v[m].Re = ve[m].Re + z.Re;
v[m].Im = ve[m].Im + z.Im;
v[m + n / 2].Re = ve[m].Re - z.Re;
v[m + n / 2].Im = ve[m].Im - z.Im;
}
}
return;
}
使用:
float temp=0;
complex v[N], scratch[N];
uint16_t k=0,m=0;
void Pwm_Irq(void)
{
temp+=0.1f;
if(temp>6.28f)
{
temp = 0;
}
motor.motor_foc.iabc.a = sin(temp);
motor.motor_foc.iabc.b = sin(temp - 2.0944f);
motor.motor_foc.iabc.c = sin(temp + 2.0944f);
v[k].Re = motor.motor_foc.iabc.a ; // 实部
v[k].Im = 0; // 虚部为0
k++;
if(k>=N)
{
k=0;
fft(v, N, scratch);
// 幅度测量
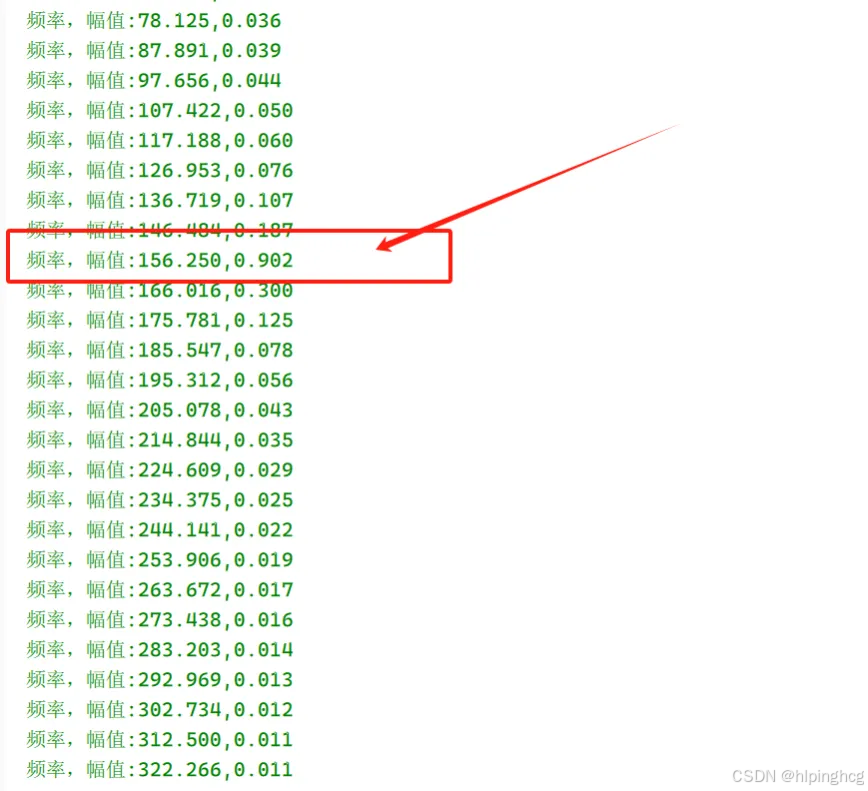
Asm_Mag(v, N);
}
}
Pwm_Irq调用频率10KHz,周期性调用。则上面正弦波的频率计算如下:
2
π
f
Δ
t
=
0.1
⇒
f
=
0.1
2
π
×
0.0001
=
159.1549
H
z
2\pi f\Delta t=0.1\Rightarrow f=\frac{0.1}{2\pi\times0.0001}=159.1549 Hz
2πfΔt=0.1⇒f=2π×0.00010.1=159.1549Hz
打印出数据可得:
3.2 matlab实现
% 生成测试信号:10Hz正弦波,采样率100Hz
Fs = 100;
t = 0:1/Fs:1-1/Fs;
f = 10;
x = sin(2*pi*f*t)+sin(4*pi*f*t);
N = 1024; % 信号长度需为2的幂
x = [x, zeros(1, N - length(x))]; % 补零至长度N
% 使用自定义FFT和MATLAB内置FFT
X_custom = my_fft(x);
X_matlab = fft(x);
% 计算误差(应接近0)
error = norm(X_custom - X_matlab);
disp(['误差范数: ', num2str(error)]);
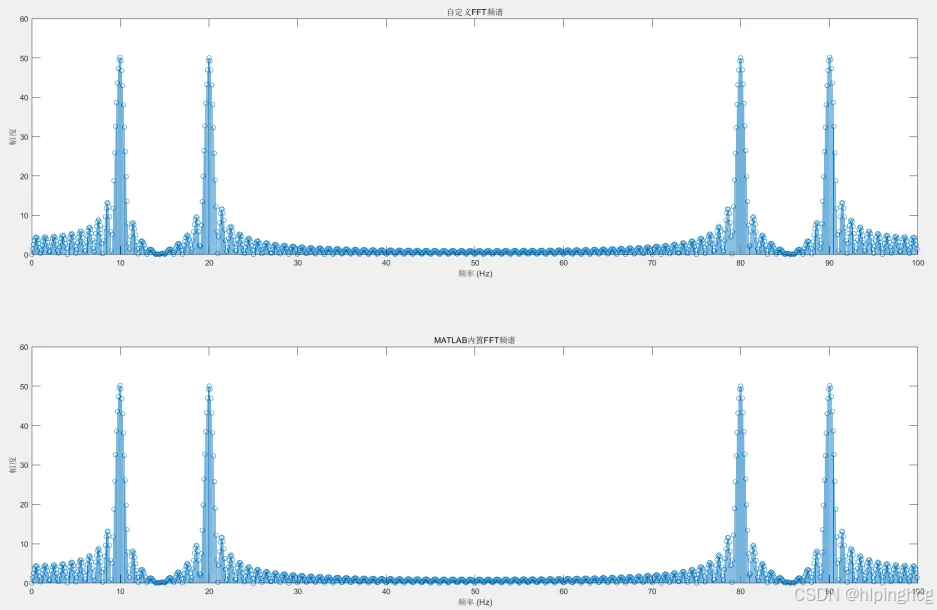
% 绘制频谱图
freq = Fs*(0:N-1)/N; % 频率轴
X_mag = abs(X_custom); % 幅度谱
figure;
subplot(2,1,1);
stem(freq, X_mag);
title('自定义FFT频谱');
xlabel('频率 (Hz)');
ylabel('幅度');
subplot(2,1,2);
stem(freq, abs(X_matlab));
title('MATLAB内置FFT频谱');
xlabel('频率 (Hz)');
ylabel('幅度');
function X = my_fft(x)
% 自定义FFT实现(递归基2 Cooley-Tukey算法)
% 输入:x为时域信号,长度需为2的整数次幂
% 输出:X为频域复数序列
N = length(x);
if N == 1
X = x; % 递归终止条件
else
even = my_fft(x(1:2:N)); % 偶数索引子序列
odd = my_fft(x(2:2:N)); % 奇数索引子序列
W = exp(-2j * pi * (0:N/2-1) / N); % 旋转因子
X = [even + W .* odd, even - W .* odd]; % 蝶形运算合并
end
end
参考
【1】雷玉飞.基于FPGA的高速、高精度FFT处理方案研究与实现[D].西安电子科技大学,2019.DOI:10.27389/d.cnki.gxadu.2019.000192.
【2】吴晨璐.面向浮点FFT的加速系统研究[D].复旦大学,2014.
【3】理解快速离散傅里叶变换算法(FFT):
https://blog.csdn.net/a358463121/article/details/127298186
【4】C语言实现离散傅里叶变换(附带源码)
https://blog.csdn.net/m0_61840987/article/details/144828163?spm=1018.2226.3001.9630.1&utm_source=vip_chatgpt_common_search_pc_result&utm_medium=distribute.pc_search_result.none-task-cask-2allinsert_cask~default-1-null.142v101pc_search_result_base6
【5】快速傅里叶变换FFT C语言实现 可用于嵌入式系统进行模拟采样频谱分析:
https://blog.csdn.net/qq_41786448/article/details/115371084