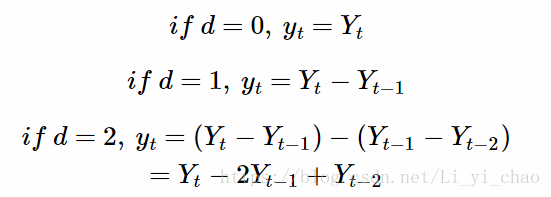解读导航:文章脉络会先以图问结合的方式,让你理解ARIMA的基本概念和术语,然后以预测下月商品销售额为实例,带你亲临建立时间序列模型的步骤和方法,之后介绍一种很有前瞻性的方法Prophet,最后总结时间序列模型的要点、技巧和注意事项。
一、用图形理解概念
ARIMA模型的全称叫做自回归移动平均模型(ARIMA, Autoregressive Integrated Moving Average Model),又称为Box-Jenkins模型。也记作ARIMA(p,d,q),是统计模型(statistic model)中最常见的一种用来进行时间序列预测的模型。
ARIMA模型其实是由AR、I、MA三者中的一个或多个组成的,p、q、d分别为对应成员的各自滞后的参数。故模型可以表示为:
其中AR是自回归模型,即在序列中的下一个值的误差(平均值的差值)是前n个值中的误差的函数。p代表预测模型中采用的时序数据本身的滞后数(lags) ,也叫做AR/Auto-Regressive项 ,一般观察PACF图决定P值大小。
AR详细可查看:https://blog.csdn.net/u010714310/article/details/81784054
MA为移动平均模型,在序列中的下一个值是前n个值的平均值的函数。q代表预测模型中采用的预测误差的滞后数(lags),也叫做MA/Moving Average项
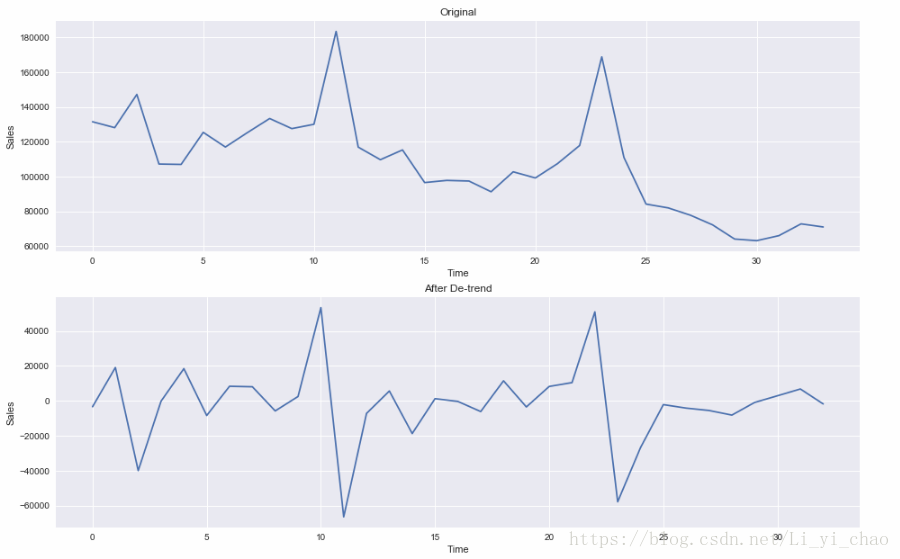
d为时间序列成为平稳时所做的差分次数。代表时序数据需要进行几阶差分化,才是稳定的。
说到这里就需要解释下差分了: 假设y表示t时刻的Y的差分。
二、 ARIMA建模基本步骤:
- 获取被观测系统时间序列数据;
- 对数据绘图,观测是否为平稳时间序列;对于非平稳时间序列要先进行d阶差分运算,化为平稳时间序列;
- 经过第二步处理,已经得到平稳