【智能算法】蜣螂优化算法（DBO）原理及实现

在这里插入图片描述

1.背景

2022年，Xue等人受到自然界中蜣螂生存行为启发，提出了蜣螂优化算法（Dung beetle optimizer, DBO）。

2.算法原理

2.1算法思想

DBO模拟了自然界蜣螂种群行为，构建了基于滚动-产卵-觅食-偷窃模型的搜索框架。
在这里插入图片描述

2.2算法过程

滚球行为：

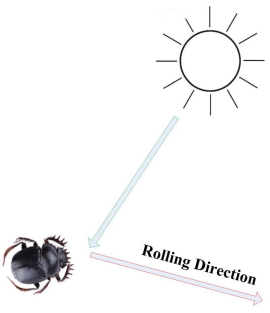
在没有障碍物的情况下，蜣螂利用太阳导航以保持粪球在直线上滚动，其中光照的强度会影响蜣螂的路径，滚球的位置更新方式：
$\begin{aligned}x_i\left(t+1\right)&=x_i\left(t\right)+\alpha\times k\times x_i\left(t-1\right)+b\times\Delta x\\\Delta x&=\left|x_i\left(t\right)-X^\mathrm{w}\right|\end{aligned}\tag{1}$
a为自然系数，a=1 表示没有偏离，a=-1 表示偏离原来方向；Xw表示全局最差位置；Δx 模拟光强的变化，越大表示光照越弱。
在这里插入图片描述

跳舞行为:

在遇到障碍物的情况下，蜣螂利用跳舞来重新定向自己，以获得新的路线，跳舞行为的位置更新方式:
$x_i\left(t+1\right)=x_i\left(t\right)+\tan(\theta)\big|x_i(t)-x_i(t-1)\big|\tag{2}$
在这里插入图片描述
繁殖行为:

雌性蜣螂将粪球滚到适合产卵的安全地方藏起来，以此为后代提供合适的栖息地:
$\begin{aligned}Lb^*&=max\Big(X^*\times\big(1-R\big),Lb\Big)\\Ub^*&=min\Big(X^*\times\big(1+R\big),Ub\Big)\end{aligned}\tag{3}$
其中，Lb*，Ub表示产卵的区域的下界和上界；X表示当前局部最优解；R=1-t/Tmax，Tmax 表示最大迭代次数；Lb，Ub 表示优化问题的下界和上界。
产卵发生的区域随迭代次数动态调整:
$B_{i}\left(t+1\right)=X^{*}+b_{1}\times\left(B_{i}\left(t\right)-Lb^{*}\right)+b_{2}\times\left(B_{i}\left(t\right)-Ub^{*}\right)\tag{4}$
其中，Bi(t)表示第 t 次迭代时第 i 个卵球的位置信息。

觅食行为：

一些成熟的蜣螂从地里钻出来寻找食物，小蜣螂的最佳觅食区域是动态更新：
$\begin{aligned}Lb^\mathrm{b}&=max\Big(X^\mathrm{b}\times\big(1-R\big),Lb\Big)\\Ub^\mathrm{b}&=min\Big(X^\mathrm{b}\times\big(1+R\big),Ub\Big)\end{aligned}\tag{5}$
其中，Xb 表示全局最优位置，Lbb，Ubb 分别表示最佳觅食区域的下界和上界。
小蜣螂的位置更新:
$x_{i}\left(t+1\right)=x_{i}\left(t\right)+C_{1}\times\left(x_{i}\left(t\right)-Lb^{\flat}\right)+C_{2}\times\left(x_{i}\left(t\right)-Ub^{\flat}\right)\tag{6}$

偷窃行为：

有些蜣螂会偷其他蜣螂的粪球，位置更新：
$x_{i}\left(t+1\right)=X^{\flat}+S\times g\times\left\{\left|x_{i}\left(t\right)-X^{\ast}\right|+\left|x_{i}\left(t\right)-X^{\flat}\right|\right\}\tag{7}$
其中，g 是大小为 1×d 服从正态分布的随机向量，S 是常量。

伪代码：
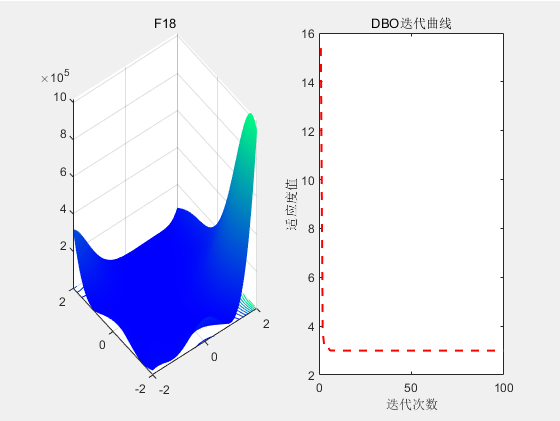
在这里插入图片描述

3.结果展示

在这里插入图片描述

4.参考文献

[1] Xue J, Shen B. Dung beetle optimizer: A new meta-heuristic algorithm for global optimization[J]. The Journal of Supercomputing, 2023, 79(7): 7305-7336.