1.背景
2023年,L Deng受到雪升华和融化行为启发,提出了雪消融优化算法(Snow Ablation Optimizer, SAO)。
2.算法原理
2.1算法思想
SAO模拟了雪的升华和融化行为,在融化过程中,雪转化为液态水,而雪可以通过升华直接转化为蒸汽。同时,融雪转化的液态水也可以通过蒸发转化为蒸汽。
2.2算法过程
探索阶段
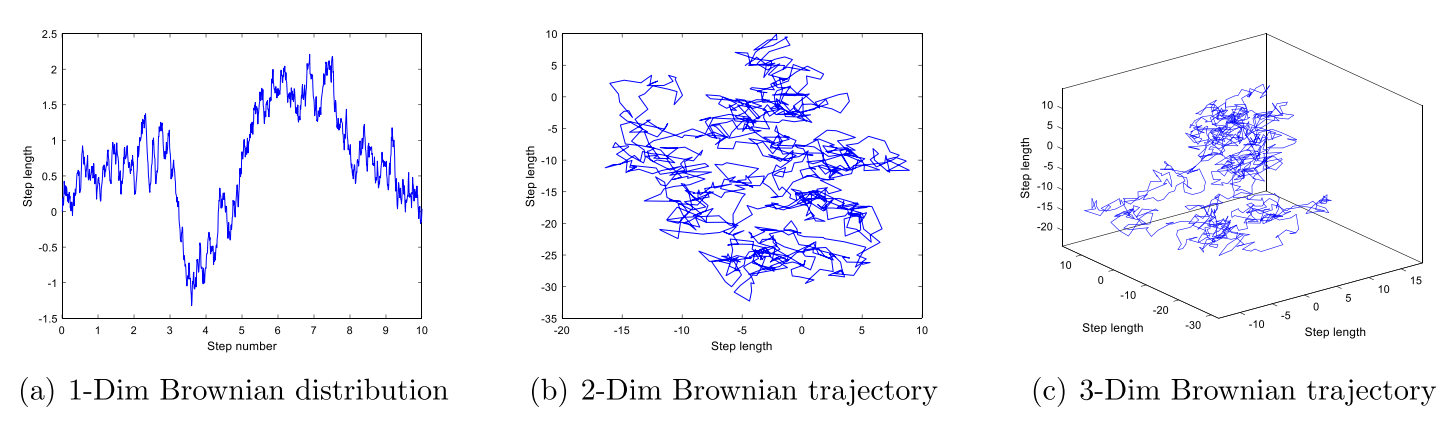
当雪或由雪转化而来的液态水转化为蒸汽时,由于运动的不规则性,搜索个体呈现出高度分散的特征。因此,这一阶段利用布朗运动来模拟这种情况:
f
B
M
(
x
;
0
,
1
)
=
1
2
π
×
exp
(
−
x
2
2
)
(1)
f_{BM}(x;0,1)=\frac1{\sqrt{2\pi}}\times\exp(-\frac{x^2}2)\tag{1}
fBM(x;0,1)=2π1×exp(−2x2)(1)
布朗运动的一维分布以及在二维和三维搜索空间中的轨迹如图,布朗运动利用动态和均匀的步长,可以探索搜索空间中的一些潜在区域。因此,它可以很好地反映蒸汽在搜索空间中扩散的情况:
Z
i
(
t
+
1
)
=
E
l
i
t
e
(
t
)
+
B
M
i
(
t
)
⊗
(
θ
1
×
(
G
(
t
)
−
Z
i
(
t
)
)
+
(
1
−
θ
1
)
×
(
Z
ˉ
(
t
)
−
Z
i
(
t
)
)
)
(2)
Z_i(t+1)=Elite(t)+BM_i(t)\otimes(\theta_1\times(G(t)-Z_i(t))+(1-\theta_1)\times(\bar{Z}(t)-Z_i(t)))\tag{2}
Zi(t+1)=Elite(t)+BMi(t)⊗(θ1×(G(t)−Zi(t))+(1−θ1)×(Zˉ(t)−Zi(t)))(2)
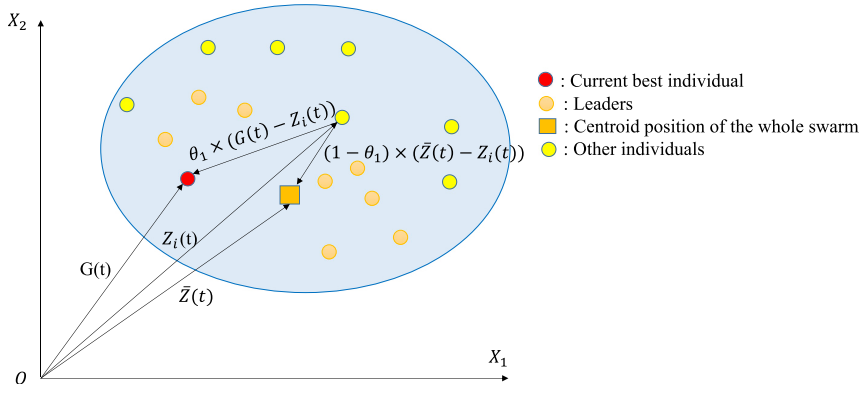
其中,G(t)当前最优解,Elite(t)代表群体中若干精英群体中随机选出的个体:
E
l
i
t
e
(
t
)
∈
[
G
(
t
)
,
Z
s
e
c
o
n
d
(
t
)
,
Z
t
h
i
r
d
(
t
)
,
Z
c
(
t
)
]
(3)
Elite(t)\in[G(t),Z_{second}(t),Z_{third}(t),Z_c(t)]\tag{3}
Elite(t)∈[G(t),Zsecond(t),Zthird(t),Zc(t)](3)
群体质心表述为:
Z
ˉ
(
t
)
=
1
N
∑
i
=
1
N
Z
i
(
t
)
(4)
\bar{Z}(t)=\frac{1}{N}\sum_{i=1}^NZ_i(t)\tag{4}
Zˉ(t)=N1i=1∑NZi(t)(4)
其中Zsecond(𝑡)和Zthird(𝑡)分别表示当前种群中的第二优个体和第三优个体。𝑍𝑐(𝑡)表示适合度值排在前50%的个体的质心位置:
Z
c
(
t
)
=
1
N
1
∑
i
=
1
N
1
Z
i
(
t
)
(5)
Z_{c}(t)=\frac{1}{N_{1}}\sum_{i=1}^{N_{1}}Z_{i}(t)\tag{5}
Zc(t)=N11i=1∑N1Zi(t)(5)
式中𝑁1表示leader的数量,即𝑁1等于整个群体的一半大小。
开发阶段
当雪通过融化行为转化为液态水时,搜索个体被鼓励围绕当前最佳解决方案开发高质量的解决方案,而不是在解决方案空间中扩展高度分散的特征。作为最经典的融雪模型之一,利用度日法来反映融雪过程:
M
=
D
D
F
×
(
T
−
T
1
)
(6)
M=DDF\times(T-T_{1})\tag{6}
M=DDF×(T−T1)(6)
其中,M为融雪速率,是模拟开发阶段融雪行为的关键参数。𝑇表示日平均温度。𝑇1为基温,基温通常设为0:
M
=
D
D
F
×
T
(7)
M=DDF\times T\tag{7}
M=DDF×T(7)
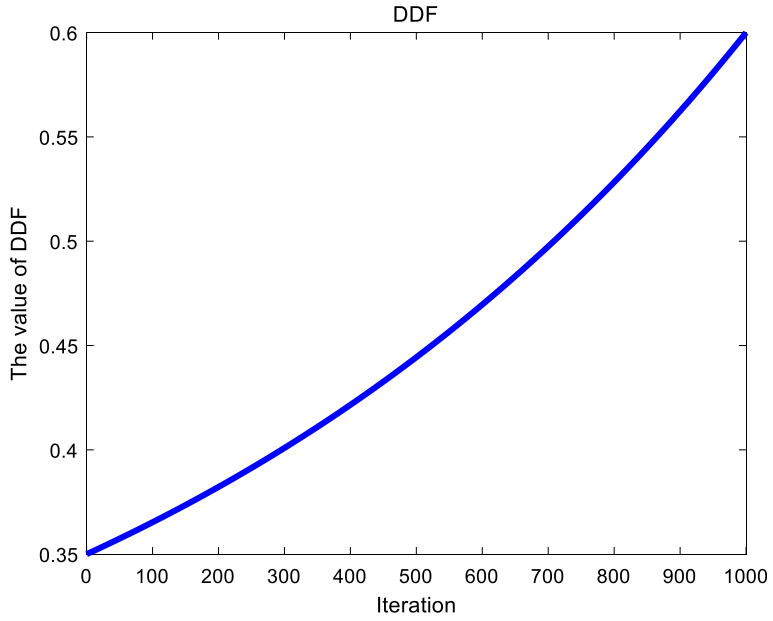
DD表述为:
D
D
F
=
0.35
+
0.25
×
e
t
t
max
−
1
e
−
1
(8)
DDF=0.35+0.25\times\frac{e^{\frac t{t_{\max}}}-1}{e-1}\tag{8}
DDF=0.35+0.25×e−1etmaxt−1(8)
融雪速率:
M
=
(
0.35
+
0.25
×
e
t
t
max
−
1
e
−
1
)
×
T
(
t
)
,
T
(
t
)
=
e
−
t
t
max
(9)
M=(0.35+0.25\times\frac{e^{\frac t{t_{\max}}}-1}{e-1})\times T(t),T(t)=e^{\frac{-t}{t_{\max}}}\tag{9}
M=(0.35+0.25×e−1etmaxt−1)×T(t),T(t)=etmax−t(9)
在SAO开发阶段,位置更新:
Z
i
(
t
+
1
)
=
M
×
G
(
t
)
+
B
M
i
(
t
)
⊗
(
θ
2
×
(
G
(
t
)
−
Z
i
(
t
)
)
+
(
1
−
θ
2
)
×
(
Z
ˉ
(
t
)
−
Z
i
(
t
)
)
)
(10)
Z_i(t+1)=M\times G(t)+BM_i(t)\otimes(\theta_2\times(G(t)-Z_i(t))+(1-\theta_2)\times(\bar{Z}(t)-Z_i(t)))\tag{10}
Zi(t+1)=M×G(t)+BMi(t)⊗(θ2×(G(t)−Zi(t))+(1−θ2)×(Zˉ(t)−Zi(t)))(10)
Dual-population机制
在元启发式算法中,实现探索与开发之间的平衡极其关键。这种平衡有助于算法不仅能发现潜在的好解决方案,而且能有效地利用这些解决方案来找到更优的结果。通过将种群分为两个子种群,一种专注于探索(寻找新的可能解),另一种专注于开发(优化已知解),这种双重人口机制有效地模拟了自然选择中的变异与遗传两大关键因素。
SAO算法的完整位置更新:
Z
i
(
t
+
1
)
=
{
E
l
i
t
e
(
t
)
+
B
M
i
(
t
)
⊗
(
θ
1
×
(
G
(
t
)
−
Z
i
(
t
)
)
+
(
1
−
θ
1
)
×
(
Z
ˉ
(
t
)
−
Z
i
(
t
)
)
)
,
i
∈
i
n
d
e
x
a
M
×
G
(
t
)
+
B
M
i
(
t
)
⊗
(
θ
2
×
(
G
(
t
)
−
Z
i
(
t
)
)
+
(
1
−
θ
2
)
×
(
Z
ˉ
(
t
)
−
Z
i
(
t
)
)
)
,
i
∈
i
n
d
e
x
b
(11)
\left.Z_{i}(t+1)=\left\{\begin{array}{c}Elite(t)+BM_i(t)\otimes(\theta_1\times(G(t)-Z_i(t))\\+(1-\theta_1)\times(\bar{Z}(t)-Z_i(t))),i\in index_a\\M\times G(t)+BM_i(t)\otimes(\theta_2\times(G(t)-Z_i(t))\\+(1-\theta_2)\times(\bar{Z}(t)-Z_i(t))),i\in index_b\end{array}\right.\right.\tag{11}
Zi(t+1)=⎩
⎨
⎧Elite(t)+BMi(t)⊗(θ1×(G(t)−Zi(t))+(1−θ1)×(Zˉ(t)−Zi(t))),i∈indexaM×G(t)+BMi(t)⊗(θ2×(G(t)−Zi(t))+(1−θ2)×(Zˉ(t)−Zi(t))),i∈indexb(11)
伪代码
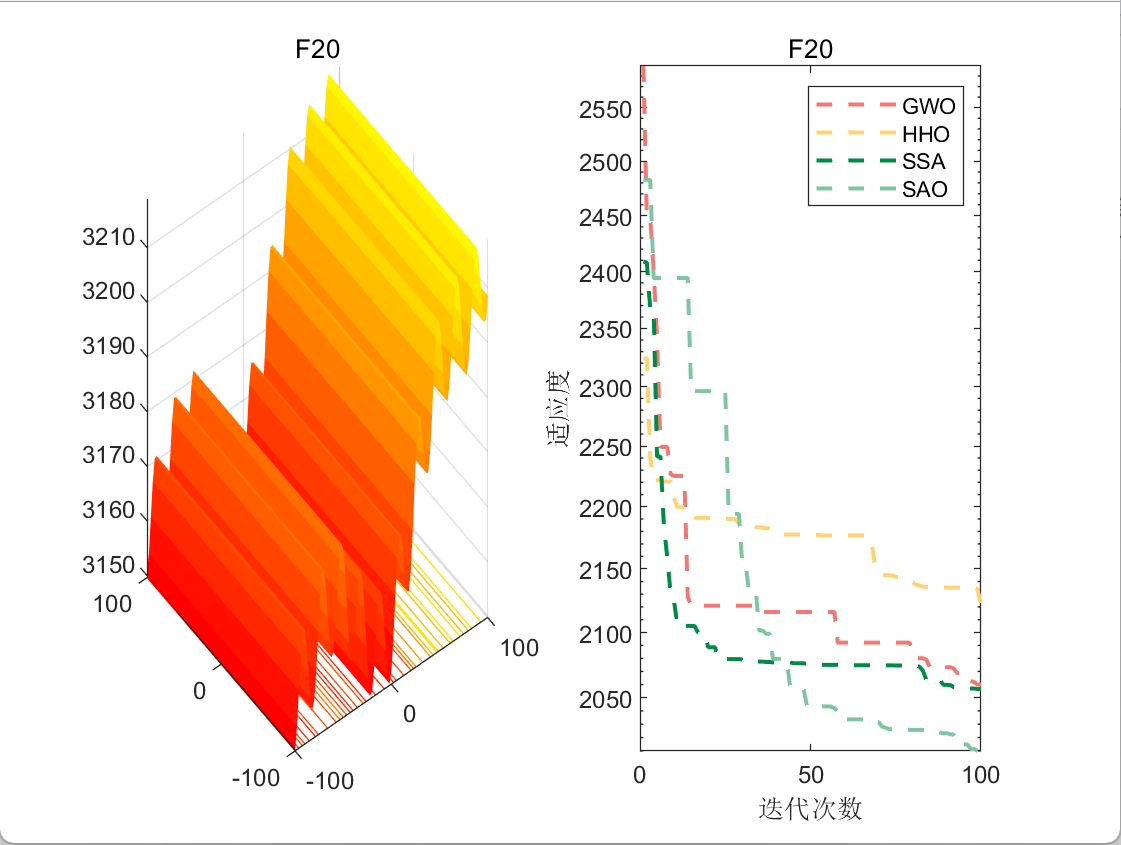
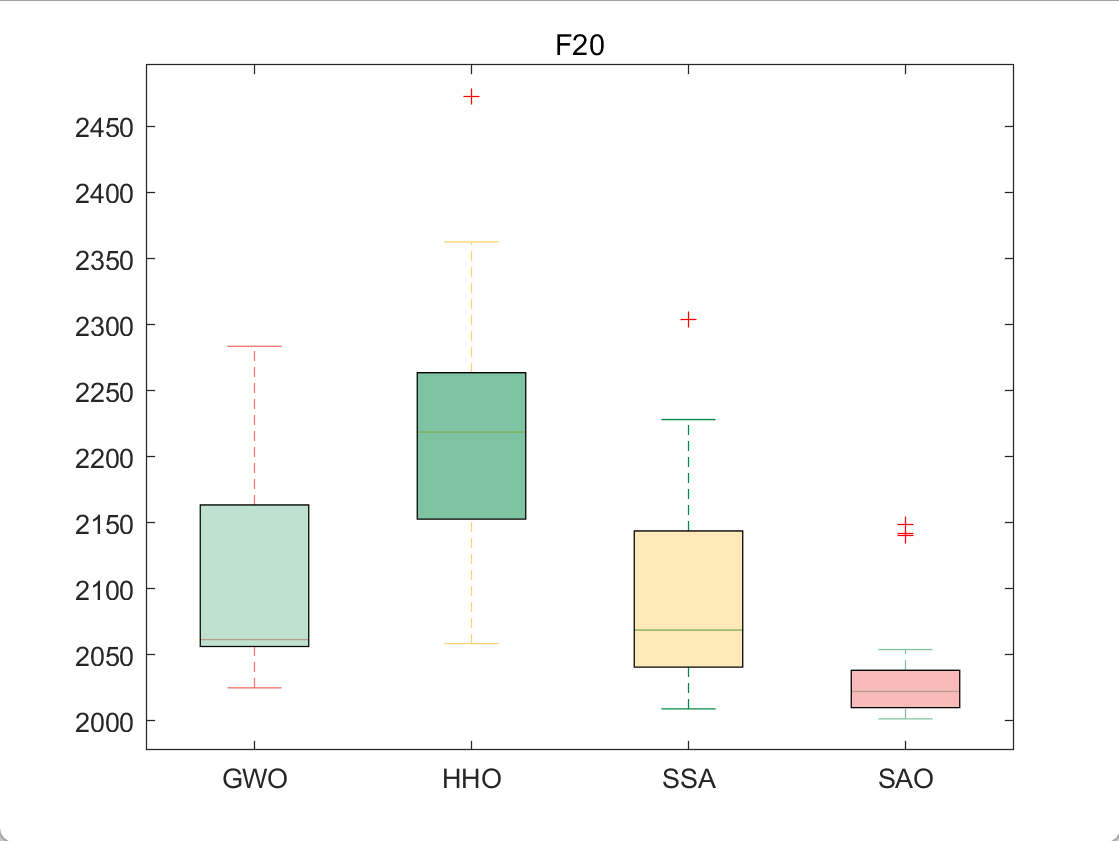
3.结果展示
使用测试框架,测试SAO性能 一键run.m
CEC2017-F20
4.参考文献
[1] Deng L, Liu S. Snow ablation optimizer: A novel metaheuristic technique for numerical optimization and engineering design[J]. Expert Systems with Applications, 2023, 225: 120069.