1.摘要
水需求预测对于促进水资源的合理利用和缓解水需求压力至关重要,本文通过深入分析水资源的使用状况,构建了三种水需求预测模型:对数模型、线性与指数组合模型以及线性、指数和对数混合模型。为了更准确地估计水资源需求,本文提出了一种融入社会学习和小波变异策略的改进型鲸鱼优化算法(SMWOA),该算法通过设计新的线性递增概率,显著提高了全局搜索的效率。根据社会学习原理,SMWOA算法利用社会排名和社会影响构建了针对个体的社会网络,并基于这种网络关系制定了自适应邻域学习策略,促进了群体间信息的有效交换与共享。此外,集成的Morlet小波变异机制能动态调整变异空间,极大增强了算法从局部最优解中逃逸的能力。
2.鲸鱼优化算法WOA原理
3.改进策略
线性递增概率
在鲸鱼优化算法(WOA)中,控制参数
∣
A
∣
|A|
∣A∣的取值范围为[0,2]。当
∣
A
∣
|A|
∣A∣大于等于1 时,算法将进行全局探索。在迭代过程的后半段(
t
≥
1
2
t
m
a
x
t\geq\frac{1}{2}t_{max}
t≥21tmax),
∣
A
∣
|A|
∣A∣的值始终小于 1,表明此时算法的全局探索能力减弱。算法通过设定
τ
=
2
(
1
−
t
t
m
a
x
)
\tau=2(1-\frac t{t_{max}})
τ=2(1−tmaxt)和
λ
=
2
r
−
1
\lambda=2r-1
λ=2r−1,进而计算
A
=
τ
⋅
λ
A=\tau\cdot\lambda
A=τ⋅λ。在整个迭代中,
∣
A
∣
≥
1
|A|\geq1
∣A∣≥1的概率为:
p
(
∣
A
∣
≥
1
)
=
0
+
∫
1
2
∫
1
/
τ
1
d
λ
d
τ
≈
0.307
p(|A|\geq1)=0+\int_1^2\int_{1/\tau}^1\mathrm{d}\lambda\mathrm{d}\tau\approx0.307
p(∣A∣≥1)=0+∫12∫1/τ1dλdτ≈0.307
考虑到鲸鱼优化算法WOA的探索能力较弱,改进SMWOA算法的搜索能力不再受到控制参数
∣
A
∣
|A|
∣A∣范围的限制。SMWOA算法的开发和探索能力是通过概率
p
r
pr
pr 控制的,此概率会随迭代次数线性增长:
p
r
=
0.5
+
z
⋅
t
t
max
p_r=0.5+z\cdot\frac{t}{t_{\max}}
pr=0.5+z⋅tmaxt
平均探索概率为:
p
ˉ
r
=
1
−
1
t
max
⋅
∑
t
=
1
t
max
(
0.5
+
0.4
⋅
t
t
max
)
=
0.3
−
0.2
t
max
\bar{p}_{r}=1-\frac{1}{t_{\max}}\cdot\sum_{t=1}^{t_{\max}}(0.5+0.4\cdot\frac{t}{t_{\max}})=0.3-\frac{0.2}{t_{\max}}
pˉr=1−tmax1⋅t=1∑tmax(0.5+0.4⋅tmaxt)=0.3−tmax0.2
自适应社会学习策略
通过应用社会学习原理,我们为每只鲸鱼构建了邻居成员关系,从而能够改变它们模仿当前最佳解决方案的行为。这种方法不仅增强了群体间的信息共享,而且提高了算法从局部最优解中跳出的能力。对于当前种群
G
(
t
)
=
{
x
1
(
t
)
,
x
2
(
t
)
,
…
,
x
N
(
t
)
}
G(t)=\{x_{1}(t),x_{2}(t),\ldots,x_{N}(t)\}
G(t)={x1(t),x2(t),…,xN(t)},根据适应度排名得到新种群
G
1
(
t
)
=
{
x
(
1
)
(
t
)
,
x
(
2
)
(
t
)
,
…
,
x
(
N
)
(
t
)
}
G_1(t)=\left\{x_{(1)}(t),x_{(2)}(t),\ldots,x_{(N)}(t)\right\}
G1(t)={x(1)(t),x(2)(t),…,x(N)(t)},每个个体在种群中的社会排名:
R
(
i
)
(
t
)
=
N
+
1
−
i
,
i
=
1
,
2
,
…
,
N
R_{(i)}(t)=N+1-i,i=1,2,\ldots,N
R(i)(t)=N+1−i,i=1,2,…,N
x
(
i
)
(
t
)
x_{(i)}(t)
x(i)(t)的社会影响为:
I
(
i
)
(
t
)
=
R
(
i
)
(
t
)
×
S
l
F
N
,
i
=
1
,
2
⋯
,
N
I_{(i)}(t)=\frac{R_{(i)}(t)\times SlF}{N},i=1,2\cdots,N
I(i)(t)=NR(i)(t)×SlF,i=1,2⋯,N
其中,
S
I
F
SIF
SIF代表社会影响因子。个体越优秀,其社会排名越高,社会影响力也越大,根据社会影响力,为种群
G
1
(
t
)
G_1(t)
G1(t)构建社会网络:
R
(
i
j
)
(
t
)
=
{
1
,
I
f
r
1
≤
max
(
i
)
(
I
(
i
)
(
t
)
,
I
(
j
)
(
t
)
)
0
,
O
t
h
e
r
w
i
s
e
R_{(ij)}(t)= \begin{cases} 1,\quad\mathrm{If}\quad r_1\leq\max_{(i)}(I_{(i)}(t),I_{(j)}(t)) \\ 0,\quad\mathrm{Otherwise} & \end{cases}
R(ij)(t)={1,Ifr1≤max(i)(I(i)(t),I(j)(t))0,Otherwise
一个个体的社会影响力越大,越多的个体会与其建立联系,这种联系网络结构使得更多的个体有机会模仿表现更优的个体的行为。通过这些个体间的联系,为个体
x
(
i
)
(
t
)
x_{(i)}(t)
x(i)(t) 建立了一个自适应的邻域网络:
N
(
i
)
(
t
)
=
{
x
(
j
)
(
t
)
∣
j
∈
[
1
,
N
]
a
n
d
j
≠
i
a
n
d
R
(
i
j
)
(
t
)
=
1
}
N_{(i)}(t)=\{x_{(j)}(t)|j\in[1,N]\mathrm{and}j\neq i\mathrm{and}R_{(ij)}(t)=1\}
N(i)(t)={x(j)(t)∣j∈[1,N]andj=iandR(ij)(t)=1}
考虑到算法的开发阶段主要集中在最佳解决方案的搜索上,而探索能力则通过群体间的协作完成,基于线性增加的概率和自适应社会邻域策略,建立了一种新的鲸鱼搜索策略:
如果
p
1
<
p
r
p_1<p_r
p1<pr,
x
(
i
j
(
t
+
1
)
=
{
x
(
1
)
j
(
t
)
−
A
⋅
d
(
i
)
j
(
t
)
r
′
<
0.5
x
(
1
)
j
(
t
)
+
e
b
l
⋅
cos
(
2
π
l
)
⋅
d
(
i
j
)
′
(
t
)
r
′
≥
0.5
\left.x_{(ij}(t+1)=\left\{ \begin{array} {cc}x_{(1)j}(t)-A\cdot d_{(i)j}(t) & r^{\prime}<0.5 \\ x_{(1)j}(t)+e^{bl}\cdot\cos(2\pi l)\cdot d_{(ij)}^{\prime}(t) & r^{\prime}\geq0.5 \end{array}\right.\right.
x(ij(t+1)={x(1)j(t)−A⋅d(i)j(t)x(1)j(t)+ebl⋅cos(2πl)⋅d(ij)′(t)r′<0.5r′≥0.5
如果
p
1
≥
p
r
p_1\geq p_r
p1≥pr,
x
(
i
j
(
t
+
1
)
=
{
x
(
1
)
j
(
t
)
−
h
(
i
)
1
r
′
<
0.5
x
(
1
)
j
(
t
)
+
h
(
i
)
2
r
′
≥
0.5
p
2
<
0.5
x_{(ij}(t+1)= \begin{cases} x_{(1)j}(t)-h_{(i)1} & r^{\prime}<0.5 \\ x_{(1)j}(t)+h_{(i)2} & r^{\prime}\geq0.5 & \end{cases}\quad p_2<0.5
x(ij(t+1)={x(1)j(t)−h(i)1x(1)j(t)+h(i)2r′<0.5r′≥0.5p2<0.5
其中,参数为:
h
(
i
)
1
=
A
⋅
∑
k
=
1
,
x
m
k
(
t
)
∈
N
(
i
)
(
t
)
K
i
w
k
⋅
(
2
r
⋅
x
(
i
)
j
(
t
)
−
x
m
k
j
(
t
)
)
h
(
i
)
2
=
e
b
l
⋅
cos
(
2
π
l
)
⋅
∑
k
=
1
,
x
m
k
(
t
)
∈
N
(
i
)
(
t
)
K
i
w
k
⋅
(
x
(
i
)
j
(
t
)
−
x
m
k
j
(
t
)
)
\begin{aligned} & h_{(i)1}=A\cdot\sum_{k=1,x_{m_k}(t)\in N_{(i)}(t)}^{K_i}w_k\cdot(2r\cdot x_{(i)j}(t)-x_{m_kj}(t)) \\ & h_{(i)2}=e^{bl}\cdot\cos(2\pi l)\cdot\sum_{k=1,x_{m_k}(t)\in N_{(i)}(t)}^{K_i}w_k\cdot(x_{(i)j}(t)-x_{m_kj}(t)) \end{aligned}
h(i)1=A⋅k=1,xmk(t)∈N(i)(t)∑Kiwk⋅(2r⋅x(i)j(t)−xmkj(t))h(i)2=ebl⋅cos(2πl)⋅k=1,xmk(t)∈N(i)(t)∑Kiwk⋅(x(i)j(t)−xmkj(t))
Morlet小波变异
小波变异通过小波函数的平移和扩展属性实现变异空间的动态调整,并提高解决方案的稳定性。通过控制小波函数的拉伸参数,减小函数的振幅,并使变异空间受到迭代次数的约束,可以实现突变操作的微调效果:
h
(
i
)
3
=
σ
j
⋅
(
u
j
−
x
(
i
)
j
(
t
)
)
h
(
i
)
4
=
σ
j
⋅
(
x
(
i
)
j
(
t
)
−
l
j
)
x
(
i
)
j
(
t
+
1
)
=
{
x
(
i
)
j
(
t
)
+
h
(
i
)
3
r
′
<
0.5
x
(
i
)
j
(
t
)
+
h
(
i
)
4
r
′
≥
0.5
p
2
≥
0.5
\begin{aligned} & h_{(i)3}=\sigma_{j}\cdot(u_{j}-x_{(i)j}(t)) \\ & h_{(i)4}=\sigma_j\cdot(x_{(i)j}(t)-l_j) \\ & x_{(i)j}(t+1)= \begin{cases} x_{(i)j}(t)+h_{(i)3} & \quad r^{\prime}<0.5 \\ x_{(i)j}(t)+h_{(i)4} & \quad r^{\prime}\geq0.5 & \end{cases} & p_{2}\geq0.5 \end{aligned}
h(i)3=σj⋅(uj−x(i)j(t))h(i)4=σj⋅(x(i)j(t)−lj)x(i)j(t+1)={x(i)j(t)+h(i)3x(i)j(t)+h(i)4r′<0.5r′≥0.5p2≥0.5
伪代码
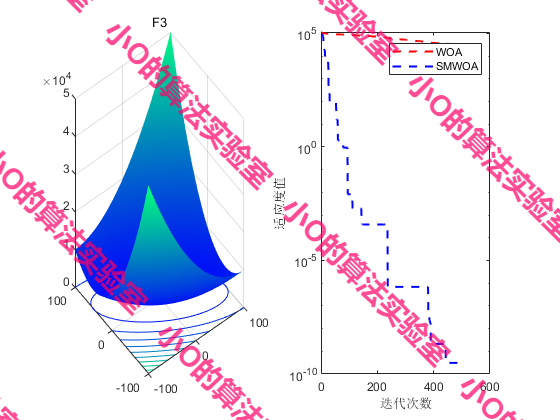
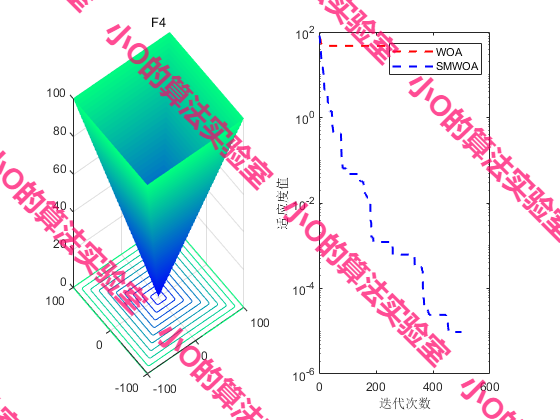
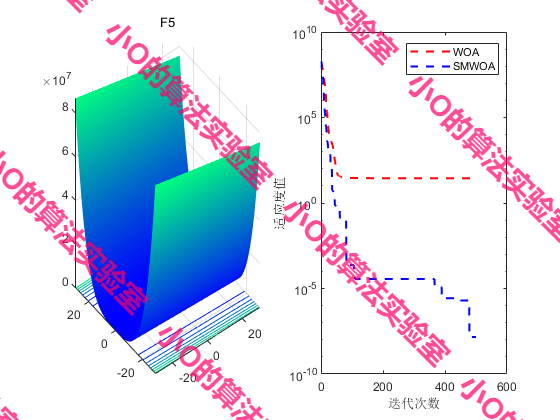
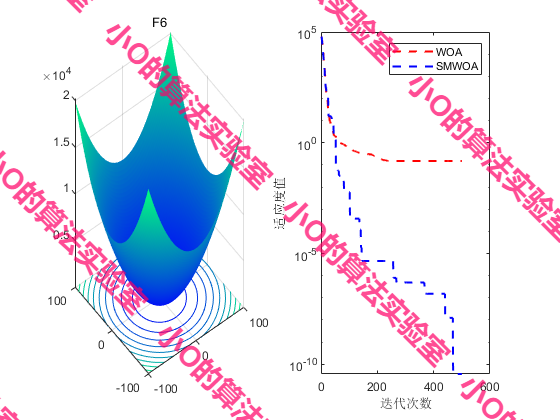
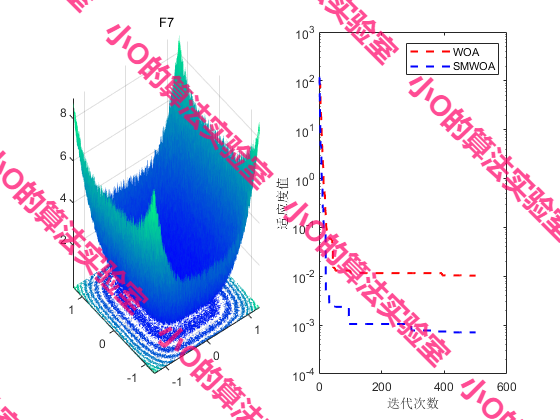
4.结果展示
5.参考文献
[1] Guo W, Liu T, Dai F, et al. An improved whale optimization algorithm for forecasting water resources demand[J]. Applied Soft Computing, 2020, 86: 105925.