数控技术 - 直线插补 - 数字积分法（DDA）

前言：还有4天要考《数控技术》了，开始（复习）预习时发现，考点之一是直线插补。这个知识点不是我上个学期的课程设计——运动控制卡的主要功能之一吗。我当时对直线插补的理解还是很简单的：一边两点取中间打折，使线段更加平滑。现在看了理论实现后发现，可以说不是一个东西了，所以甚是感觉有趣。

排除掉要应付大学考试，直线插补这个知识点还是很主要的。特地写篇笔记记录，防止以后忘记。

• 推荐视频：《逐点比较法-478-机床数控系统综合设计-远程教育|夜大|面授|函授|家里蹲大学|宅在家|在家宅_哔哩哔哩_bilibili》北京理工大学老师讲解，up主应该是转载或代传。

1.解释

• 积分的概念不过多说明，不是重点。只需明白是 周期性累加值 即可。

• 数字积分法的操作很简单，就是将路程分割n份，每 周期 累加一份，如果 溢出 就进给。一般溢出值就是单位1，大概因为是坐标系的分度值，起点终点也在整数坐标上。

类比逐点比较法，同样是累加，不过 数字积分法 只 累加正数 。同样有个分割线，不过不是零而是 溢出值 。

• 注意 ！累加 是每周期都会固定进行的操作，进给 是只有在溢出时才会进行的操作。

• 重要定义： 各轴 累加计算都是 独立 进行的，是否进给也是 独立 的，相互之间不影响！可能各轴都进给，也可能 各轴 都不进给。

类比逐点比较法，因为比较偏差是通过斜率反应，进给也是每次只能选一个轴方向。所以逐点比较法只适用于平面，局限性很大，但是简单易用。数字积分法则不限于两轴，可多轴运用，适用空间运动。

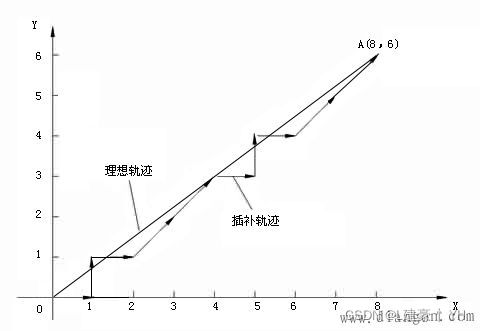
• 因为各轴独立运动，运动轨迹就是各轴运动的合成效果，会出现斜线。比如45°。看起来也更加接近理想曲线。下图示意，来源网络。

2.计算

• 正如上面所说，只需要将各轴的路程统一分割n份，再周期累加，溢出就进给即可。列个表格一下子就清晰了。

例题：第一象限直线OE，起点为O(0，0)，终点为E(6，3)。

1. 试着X轴和Y轴路程分割8份试试。然后累加8次，就得到结果。

2. 小数形式不方便运算，避免使用浮点数。可以采用整体放大的方法，溢出值和累加值都乘以相同倍数即可。就相当于去分母操作，同时乘于8。

和逐点比较法类似，起点和终点的计算结果都是0。

3. 分割几份不是一定的，下面示例分割16份看看。作图的话，会发现轨迹图和分割8份是一样。从列表中也可以发现二者是存在比例性的。

• 分割10份也可以，只要分割后的每份不能超过溢出值1即可，

$$(\frac{x_e}{N}<1)\&\&(\frac{y_e}{N}<1)$$

• 虽然分割分数不一定，但是肯定越少越好，计算过程简单点。在数控技术中，这个分割份数是有讲究的，也是原理的一部分。下面讲解如何计算 最小 的分割份数。

3.原理

以下内容是视频教程中老师讲的思路，例图我也是截图引用了。

1. 因为各轴相互独立运动，实际运动是合成结果，所以速度和路程存在一个比例关系。

注意 ：上图中的k只是代表系数，并不是指斜率。一开始没认真听，还懵逼了好久。为了避免这个问题，我下面采用a代表这个系数。

$$\frac{V_x}{X_e}=\frac{V_y}{Y_e}=\frac{V}{\sqrt[2]{X_e^2+Y_e^2}}=\frac{V}{OE}=a$$

2. 根据上面的比例关系，可以得到两个等式。

$$\begin{gathered} V_x=a\ast X_e \\ {V}_y=a\ast Y_e \end{gathered}$$

3. 然后就可以表示每周期的微小 累加量 ，也就是分割份数后每一份。另外，微小的时间周期可以取1。

$$\begin{gathered} \Delta X=V_x\ast \Delta t=a\ast X_e\ast \Delta t=a\ast X_e \\ \Delta Y=V_y\ast \Delta t=a\ast Y_e\ast \Delta t=a\ast X_e \end{gathered}$$

4. 再假设分割的总份数为m，那么总位移量就可以表示了。

$$\begin{gathered} X_e=m\ast \Delta X=m\ast a\ast X_e \\ {Y}_e=m\ast \Delta Y=m\ast a\ast Y_e \end{gathered}$$

5. 上式明显可以化简，那么就得到了分割份数m和系数a之间关系了。

$$1=m\ast a$$

6. 回顾第3步得到的累加量，之前讲原理时也提到，这个累加量是不能大于溢出值1的。不然就没有累加和溢出的意义了。

$$\begin{gathered} 1>\Delta X=a\ast X_e=\frac{1}{m}\ast X_e \\ 1>\Delta Y=a\ast Y_e=\frac{1}{m}\ast Y_e \end{gathered}$$

7. 因为不等式最终要小于1，要使不等式成立，取X_e和Y_e其中的最大值Max，计算最小值m即可。

$$m>Max$$

其实也很好明白，反过去想，因为分割是路程除以份数。要想这个值小于1，只要份数比最大路程还大，算出来就一定小于1。同时份数要尽可能的小。

8. 最后，为了方便计算，不除以分割数，而是乘于分割数，放大倍数计算。

4.数控技术

• 在数控技术中，对于分割数m还是有特别要求的，牵扯到 寄存器 的概念。

• 因为实际运用问题，机器在存储数据时是采用二进制的形式。为了节省空间和加快运算，Max是多少，就采用多少位的 累加器 运算。也就是2^n-1，能放得下即可。比如终点E(7,5)，Max为7，采用三位（最大可存8）累加器计算。

• 所以分割份数m总是2的次方，而且列表时也不写十进制，而是写二进制。

考试做题时，题目会直接给出几位累加器，且使用DDA计算。

5.补充

• 其他象限的情况和逐点比较法类似，取绝对值计算。得到相对进给方向，然后对应的象限给轴进给即可。