【k近邻算法】

k近邻法

k近邻算法简介
- 认识k近邻算法

k近邻算法简介

认识k近邻算法

1.1 k近邻算法，英：(fc-nearest neighbor, fc-NN)也是一种基本分类的逻辑算法。主要从 $k$ 近邻法的特征输入为实例的特征向量，相对于特征空间的点，通过这些点输出一些实例。在运用k近邻算法时，我们也可以取多类，其目的预测的实例更为精确。
1.2 k近邻算法相对简单，同样给定一个数据训练集，不断训练这些数据集，在这些实例中找到与邻近的k的这个实例。注：这些实例大部分属于某个类，从而把该输入划分为这个类。
1.3 数据样本：
输入：
$T={(x_1,y_1),(x_2,y_2)....(x_n,y_n)}$
注：其中的 $x_i∈X⊆R^n$ 称为实例的特征向量， $y_i∈y={c_1,c_2...c_k}$ ,i∈N.
输出：
实例x的所属类 $y$
(1)通过距离度量，在样本 $T$ 中找出与 $x$ 最邻近的k个点，把k个 $x$ 点的领域称 $N_k(x)$
(2)在 $N_k(x)$ 中根据分类决策规则，从而决定x的类别y
公式为：
$\underset {c_j}{max}\sum\limits_{x_i∈N_k(x)}I(y_i=c_j),i∈N,j∈k$
注：其中 $I 为指示函数$ ，当 $y_i=c_j$ 时， $I$ 为1，否则为0。
特别注意：k近邻点法没有显式的学习过程。

K-近邻算法三要素

1.三要素：
k 值的选择、距离度量和分类决策规则
2.模型
K-近邻模型：
**KNN中，当训练集、距离度量、k值及分类决策规则确定后，对于任何一个新的输入实例，它所属的类唯一地确定。**这相当于根据上述要素将特征空间划分为一些子空间,确定子空间里的每个点所属的类。
单元(cell)：特征空间中对每个训练实例点x，距离该点比其他点更近的所有点组成的一个区域叫做单元。
类标记( classlabel)：每个训练实例点拥有一个单元，所有训练实例点的单元构成对特征空间的一个划分。最近邻法将实例$ x_i $的类作为其单元中所有点的类$ $y_i$ 标记( classlabel)。这样,每个单元的实例点的类别是确定的。图3.1是二维特征空间划分的一个例子。
代码实现：

import csv
import random
import math
import operator

# 加载数据集
def loadDataset(filename, split, trainingSet = [], testSet = []):
    with open(filename, 'r') as csvfile:
        lines = csv.reader(csvfile)
        dataset = list(lines)
        for x in range(len(dataset)-1):
            for y in range(4):
                dataset[x][y] = float(dataset[x][y])
            if random.random() < split:  #将数据集随机划分
                trainingSet.append(dataset[x])
            else:
                testSet.append(dataset[x])

# 计算点之间的距离，多维度的
def euclideanDistance(instance1, instance2, length):
    distance = 0
    for x in range(length):
        distance += pow((instance1[x]-instance2[x]), 2)
    return math.sqrt(distance)

# 获取k个邻居
def getNeighbors(trainingSet, testInstance, k):
    distances = []
    length = len(testInstance)-1
    for x in range(len(trainingSet)):
        dist = euclideanDistance(testInstance, trainingSet[x], length)
        distances.append((trainingSet[x], dist))   #获取到测试点到其他点的距离
    distances.sort(key=operator.itemgetter(1))    #对所有的距离进行排序
    neighbors = []
    for x in range(k):   #获取到距离最近的k个点
        neighbors.append(distances[x][0])
        return neighbors

# 得到这k个邻居的分类中最多的那一类
def getResponse(neighbors):
    classVotes = {}
    for x in range(len(neighbors)):
        response = neighbors[x][-1]
        if response in classVotes:
            classVotes[response] += 1
        else:
            classVotes[response] = 1
    sortedVotes = sorted(classVotes.items(), key=operator.itemgetter(1), reverse=True)
    return sortedVotes[0][0]   #获取到票数最多的类别

#计算预测的准确率
def getAccuracy(testSet, predictions):
    correct = 0
    for x in range(len(testSet)):
        if testSet[x][-1] == predictions[x]:
            correct += 1
    return (correct/float(len(testSet)))*100.0

def main():
    #prepare data
    trainingSet = []
    testSet = []
    split = 0.67
    loadDataset(r'irisdata.txt', split, trainingSet, testSet)
    print('Trainset: ' + repr(len(trainingSet)))
    print('Testset: ' + repr(len(testSet)))
    #generate predictions
    predictions = []
    k = 3
    for x in range(len(testSet)):
        # trainingsettrainingSet[x]
        neighbors = getNeighbors(trainingSet, testSet[x], k)
        result = getResponse(neighbors)
        predictions.append(result)
        print ('predicted=' + repr(result) + ', actual=' + repr(testSet[x][-1]))
    print('predictions: ' + repr(predictions))
    accuracy = getAccuracy(testSet, predictions)
    print('Accuracy: ' + repr(accuracy) + '%')

if __name__ == '__main__':
    main()

习题3.1

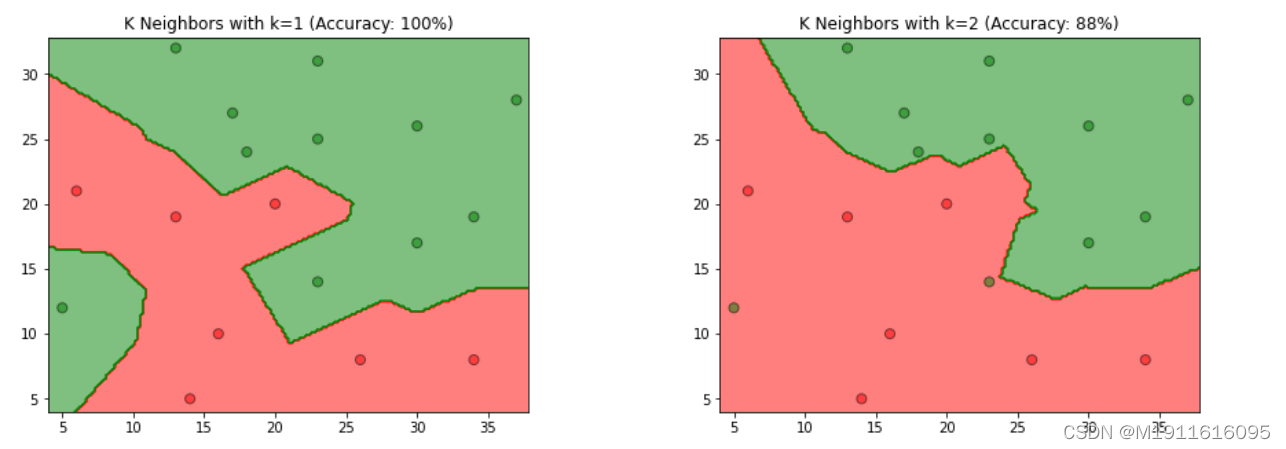
1.题目：参照图3.1，在二维空间中给出实例点，画出kk为1和2时的kk近邻法构成的空间划分，并对其进行比较，体会kk值选择与模型复杂度及预测准确率的关系。
2.思路：

1.参照图3.1，使用已给的实例点，采用sklearn的KNeighborsClassifier分类器，对k=1和2时的模型进行训练
2.使用matplotlib的contourf和scatter，画出k为1和2时的k近邻法构成的空间划分
3.根据模型得到的预测结果，计算预测准确率，并设置图形标题
4.根据程序生成的图，比较k为1和2时，k值选择与模型复杂度、预测准确率的关系
3.代码

from matplotlib.colors import ListedColormap
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier
import numpy as np
%matplotlib inline

data = np.array([[5, 12, 1],
                 [6, 21, 0],
                 [14, 5, 0],
                 [16, 10, 0],
                 [13, 19, 0],
                 [13, 32, 1],
                 [17, 27, 1],
                 [18, 24, 1],
                 [20, 20, 0],
                 [23, 14, 1],
                 [23, 25, 1],
                 [23, 31, 1],
                 [26, 8, 0],
                 [30, 17, 1],
                 [30, 26, 1],
                 [34, 8, 0],
                 [34, 19, 1],
                 [37, 28, 1]])
# 得到特征向量
X_train = data[:, 0:2]
# 得到类别向量
y_train = data[:, 2]

#（1）使用已给的实例点，采用sklearn的KNeighborsClassifier分类器，
# 对k=1和2时的模型进行训练
# 分别构造k=1和k=2的k近邻模型
models = (KNeighborsClassifier(n_neighbors=1, n_jobs=-1),
          KNeighborsClassifier(n_neighbors=2, n_jobs=-1))
# 模型训练
models = (clf.fit(X_train, y_train) for clf in models)

# 设置图形标题
titles = ('K Neighbors with k=1',
          'K Neighbors with k=2')

# 设置图形的大小和图间距
fig = plt.figure(figsize=(15, 5))
plt.subplots_adjust(wspace=0.4, hspace=0.4)

# 分别获取第1个和第2个特征向量
X0, X1 = X_train[:, 0], X_train[:, 1]

# 得到坐标轴的最小值和最大值
x_min, x_max = X0.min() - 1, X0.max() + 1
y_min, y_max = X1.min() - 1, X1.max() + 1

# 构造网格点坐标矩阵
# 设置0.2的目的是生成更多的网格点，数值越小，划分空间之间的分隔线越清晰
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.2),
                     np.arange(y_min, y_max, 0.2))

for clf, title, ax in zip(models, titles, fig.subplots(1, 2).flatten()):
    # （2）使用matplotlib的contourf和scatter，画出k为1和2时的k近邻法构成的空间划分
    # 对所有网格点进行预测
    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    # 设置颜色列表
    colors = ('red', 'green', 'lightgreen', 'gray', 'cyan')
    # 根据类别数生成颜色
    cmap = ListedColormap(colors[:len(np.unique(Z))])
    # 绘制分隔线，contourf函数用于绘制等高线，alpha表示颜色的透明度，一般设置成0.5
    ax.contourf(xx, yy, Z, cmap=cmap, alpha=0.5)

    # 绘制样本点
    ax.scatter(X0, X1, c=y_train, s=50, edgecolors='k', cmap=cmap, alpha=0.5)

    # （3）根据模型得到的预测结果，计算预测准确率，并设置图形标题
    # 计算预测准确率
    acc = clf.score(X_train, y_train)
    # 设置标题
    ax.set_title(title + ' (Accuracy: %d%%)' % (acc * 100))

plt.show()

输出结果：
在这里插入图片描述
第4步：比较kk为1和2时，k值选择与模型复杂度、预测准确率的关系
kk值选择与模型复杂度的关系
根据书中第52页（3.2.3节：kk值的选择）
4.1综上所属，kk值越大，模型复杂度越低，模型越简单，容易发生欠拟合。反之，kk值越小，模型越复杂，容易发生过拟合。

4.2kk值选择与预测准确率的关系
从图中观察到，当k=1k=1时，模型易产生过拟合，当k=2k=2时准确率仅有88%，故在过拟合发生前，kk值越大，预测准确率越低，也反映模型泛化能力越差，模型简单。反之，kk值越小，预测准确率越高，模型具有更好的泛化能力，模型复杂

习题3.2

1.题目：利用例题3.2构造的kdkd树求点 $x=(3,4.5)^T$
的最近邻点
2.思路：
方法一：
使用sklearn的KDTree类，结合例题3.2构建平衡kdkd树，配置相关参数（构建平衡树kd树算法，见书中第54页算法3.2内容）；
使用tree.query方法，查找(3, 4.5)的最近邻点（搜索kd树算法，见书中第55页第3.3.2节内容）；
根据第3步返回的参数，得到最近邻点。
方法二：
根据书中第56页算法3.3用kdkd树的最近邻搜索方法，查找(3, 4.5)的最近邻点
方法一：

import numpy as np
from sklearn.neighbors import KDTree

# 构造例题3.2的数据集
train_data = np.array([[2, 3],
                      [5, 4],
                      [9, 6],
                      [4, 7],
                      [8, 1],
                      [7, 2]])
# （1）使用sklearn的KDTree类，构建平衡kd树
# 设置leaf_size为2，表示平衡树
tree = KDTree(train_data, leaf_size=2)

# （2）使用tree.query方法，设置k=1，查找(3, 4.5)的最近邻点
# dist表示与最近邻点的距离，ind表示最近邻点在train_data的位置
dist, ind = tree.query(np.array([[3, 4.5]]), k=1)
node_index = ind[0]

# （3）得到最近邻点
x1 = train_data[node_index][0][0]
x2 = train_data[node_index][0][1]
print("x点(3,4.5)的最近邻点是({0}, {1})".format(x1, x2))

输出结果：

x点(3,4.5)的最近邻点是(2, 3)

方法二：

找到点 $x=(3,4.5)^Tx$ 所在领域的叶节点 $x_1=(4,7)^Tx _1$ ，则最近邻点一定在以x为圆心，x到 $x_1$ 距离为半径的圆内；找到 $x_1$ 的父节点 $x_2=(5,4)^Tx _2=(5,4) ^T，x_2$ 的另一子节点为 $x_3=(2,3)^Tx _3$ ， $此时x_3在圆内，故x_3 为最新的最近邻点，并形成以xx为圆心，以xx到x_3 距离为半径的圆；继续探索x_2的父节点x_4=(7,2)^Tx_4=(7,2) ^T4$ 的另一个子节点(9,6)(9,6)对应的区域不与圆相交，故不存在最近邻点，所以最近邻点为 $x_3=(2,3)^Tx _3 =(2,3) ^T$
。可得到点 $x=(3,4.5)^T,x=(3,4.5) ^T$ 的最近邻点是 $2,3)^T(2,3) ^T$