【引入】
有些$DP$方程可以转化成$f[i]=f[j]+x[i]$的形式,其中$f[j]$中保存了只与$j$相关的量。这样的$DP$方程我们可以用单调队列进行优化,从而使得$O(n^2)$的复杂度降到$O(n)$。
但像这样的方程:$dp[i]=dp[j]+(x[i]-x[j])×(x[i]-x[j])$。如果把右边的乘法化开的话,会得到$x[i]×x[j]$的项。它不能分解为只与$i$或$j$有关的部分。若用单调队列优化方法就不好使了。
这里学习一种新的优化方法,叫做斜率优化。
【例题】HDU 3507 print artical
【题目大意】
输出$N$个数字$a[N]$,输出的时候可以连续的输出,每连续输出一串,它的费用是 “这串数字和的平方加上一个常数$M$”。其中$N≤500000$。
【例题分析】
对于这样一个题目,我们先规定以下变量:
- $dp[i]$:输出到$i$的时候最少的花费
- $sum[i]$:从$a[1]$到$a[i]$的数字和。
于是方程就是:$$dp[i]=dp[j]+M+(sum[i]-sum[j])^2$$
很显然这个$DP$式时间复杂度为$O(N^2)$。题目的数字有$500000$个,很明显,若不对这个$DP$式加以修饰,是一定会超时的。
那么该怎么办呢?这下就需要我们的斜率优化对于$O(N^2)$的时间复杂度降维。
首先,我们对这个式子化简:
我们考虑两个决策点$k$与$j$,如果决策$j$更优,那么也就是
$$dp[j]+M+(sum[i]-sum[j])^2<dp[k]+M+(sum[i]-sum[k])^2$$
消去共同项,得:
$$dp[j]+sum[j]^2-2×sum[i]×sum[j]<dp[k]+sum[k]^2-2×sum[i]×sum[k]$$
即$$dp[j]+sum[j]^2-(dp[k]+sum[k]^2)<2×sum[i]×(sum[j]-sum[k])$$
若$j>k$,则$$sum[j]-sum[k]>0$$
可得$${\frac{{dp\text{[}j\text{]}+sum\text{[}j\mathop{{\text{]}}}\nolimits^{{2}}-\text{(}dp\text{[}k\text{]}+sum\text{[}k\mathop{{\text{]}}}\nolimits^{{2}}\text{)}}}{{2 \times \text{(}sum\text{[}j\text{]}-sum\text{[}k\text{]}\text{)}}}}<sum[i]$$
反之,若$j<k$,则$$sum[j]-sum[k]<0$$
则可得$$
{\frac{{dp\text{[}j\text{]}+sum\text{[}j\mathop{{\text{]}}}\nolimits^{{2}}-\text{(}dp\text{[}k\text{]}+sum\text{[}k\mathop{{\text{]}}}\nolimits^{{2}}\text{)}}}{{\left. 2*\text{(}sum\text{[}j\text{]}-sum\text{[}k\text{]} \right) }}}>sum[i]$$
我们把$dp[j]+sum[j]^2$看做是$y_j$,把$2×sum[j]$看成是$x_j$。
左边$\frac{y_j-y_k}{x_j-x_k}$似乎是斜率的表示?
若$j>k$,则$\frac{y_j-y_k}{x_j-x_k}<sum[i]$等价于决策$j$优于$k$。
若$j<k$,则$\frac{y_j-y_k}{x_j-x_k}>sum[i]$等价于决策$j$优于$k$。
感性理解就是:如果两个决策点的斜率小于$sum[i]$,则靠后的决策点更优;否则靠前的决策点更优。
更强的性质:
若有三个决策点,满足$k<j<i$且$g[i,j]<g[j,k]$,则$j$点永远不可能成为最优决策点,可以直接将它从决策点集合中去掉。
但是这是为什么呢?
分三种情况讨论:
设当前点为$a$
- 如果$g[i,j]$与$g[j,k]$均小于$sum[a]$,则$i$比$j$优,$j$比$k$。
- 如果$g[i,j]$与$g[j,k]$均大于$sum[a]$,则$k$比$j$优,$j$比$i$优。
- 如果$g[i,j]<sum[a]$且$g[i,j]>sum[a]$,则$i$比$j$优,$k$比$j$优。
不论如何,$j$都无法成为最佳决策点,所以可以排除$j$。
于是,所有的决策点满足一个下凸包性质。
接下来看看如何找最优解。
设$k<j<i$。
由于我们排除了$g[i,j]<g[j,k]$的情况,所以整个有效点集呈现一种下凸性质,即$g[i,j]>g[j,k]$。
这样,从左到右,斜率之间就是单调递增的了。当我们的最优解取得在$j$点的时候,那么$k$点不可能再取得比$j$点更优的解了,于是$k$点也可以排除。
换句话说,$j$点之前的点全部不可能再比$j$点更优了,可全部从解集中排除。这是为什么呢?因为$sum[i]$随着$i$的增长也是单调递增的。
所以,对于两个决策点$j$和$k$,设$j<k$。如果$k$优于$j$,则以后$k$永远优于$j$,则$j$及之前的决策点都可以删除了。

- 用一个单调队列来维护解集。
- 假设队列中从头到尾已经有元素$a,b,c$。那么当$d$要入队的时候,我们维护队列的下凸性质,即如果$g[d,c]<g[c,b]$,那么就将$c$点删除。直到找到$g[d,x]≥g[x,y]$为止,并将$d$点加入在该位置中。
- 找最佳决策点时,设当前求解状态为$i$,从队头开始,如果已有元素$a,b,c$,当i点要求解时,如果$g[b,a]<sum[i]$,那么说明$b$点比$a$点更优,$a$点可以排除,于是$a$出队,直到第一次遇到$g[j,j-1]>sum[i]$,此时$j-1$即为最佳决策点。
设有三个点$i,j,k$。其中$x_i>x_j>x_k$。如何判断三点是上凸还是下凸?
用向量的叉积运算即可。
向量可以看做是二维平面坐标中的有向线段。向量的起点可以自由选择,即可以把它在平面内任意平移。平移过后的向量与原平移前完全等价。
如果一条有向线段的起点为$(x_1,y_1)$,终点为$(x_2,y_2)$。我们可以将它平移,使得起点位置为$(0,0)$,终点位置为$(x_2-x_1,y_2-y_1)$。
此时向量的大小和方向不变。我们以后谈及向量,都默认它的起点在$(0,0)$处,而只以它的终点表示该向量。
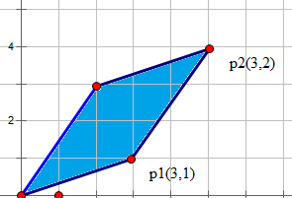
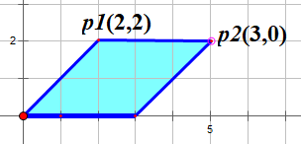
设有向量$p_1(x_1,y_1)$,$p_2(x_2,y_2)$。他们的叉乘为$p_1×p_2=(x_1*y_2-x_2*y_1)$。
叉乘的物理意义为以向量$p_1$和$p_2$为相邻两边的平行四边形的有向面积。
左图为正向有向面积,右图为负向有向面积。
平面四边形在两向量的顺时针方向,则为正,反之则为负。如何判断$p_1$与$p_2$的位置关系?
- 若$p_1×p_2>0$,则$p_2$在$p_1$的逆时针方向;
- 若$p_1×p_2<0$,则$p_2$在$p_1$的顺时针方向;
- 若$p_1×p_2=0$,则$p_1$与$p_2$方向重合。
所以我们可以令向量$p_1=(x_j-x_k,y_j-y_k),p_2=(x_i-x_j,y_j-y_k)$,再用叉积即可判断$i,j,k$是上凸还是下凸。
另外注意:比较斜率避免用除法。
下见代码
#include<iostream> #include<string> using namespace std; int dp[500005]; int q[500005]; int sum[500005]; int head,tail,n,m; int getDP(int i,int j) { return dp[j]+m+(sum[i]-sum[j])*(sum[i]-sum[j]); } int getUP(int j,int k) //yj-yk的部分 { return dp[j]+sum[j]*sum[j]-(dp[k]+sum[k]*sum[k]); } int getDOWN(int j,int k) //xj-xk的部分 { return 2*(sum[j]-sum[k]); } int main() { int i; while(scanf("%d%d",&n,&m)==2) { for(i=1;i<=n;i++) scanf("%d",&sum[i]); sum[0]=dp[0]=0; for(i=1;i<=n;i++) sum[i]+=sum[i-1]; head=tail=0; q[tail++]=0; for(i=1;i<=n;i++) { while(head+1<tail && getUP(q[head+1],q[head])<=sum[i]*getDOWN(q[head+1],q[head])) head++; dp[i]=getDP(i,q[head]); while(head+1<tail && getUP(i,q[tail-1])*getDOWN(q[tail-1],q[tail-2])<=getUP(q[tail-1],q[tail-2])*getDOWN(i,q[tail-1])) tail--; q[tail++]=i; } printf("%d\n",dp[n]); } return 0; }
练习题:
$HDU2829,HDU3480,POJ3709$