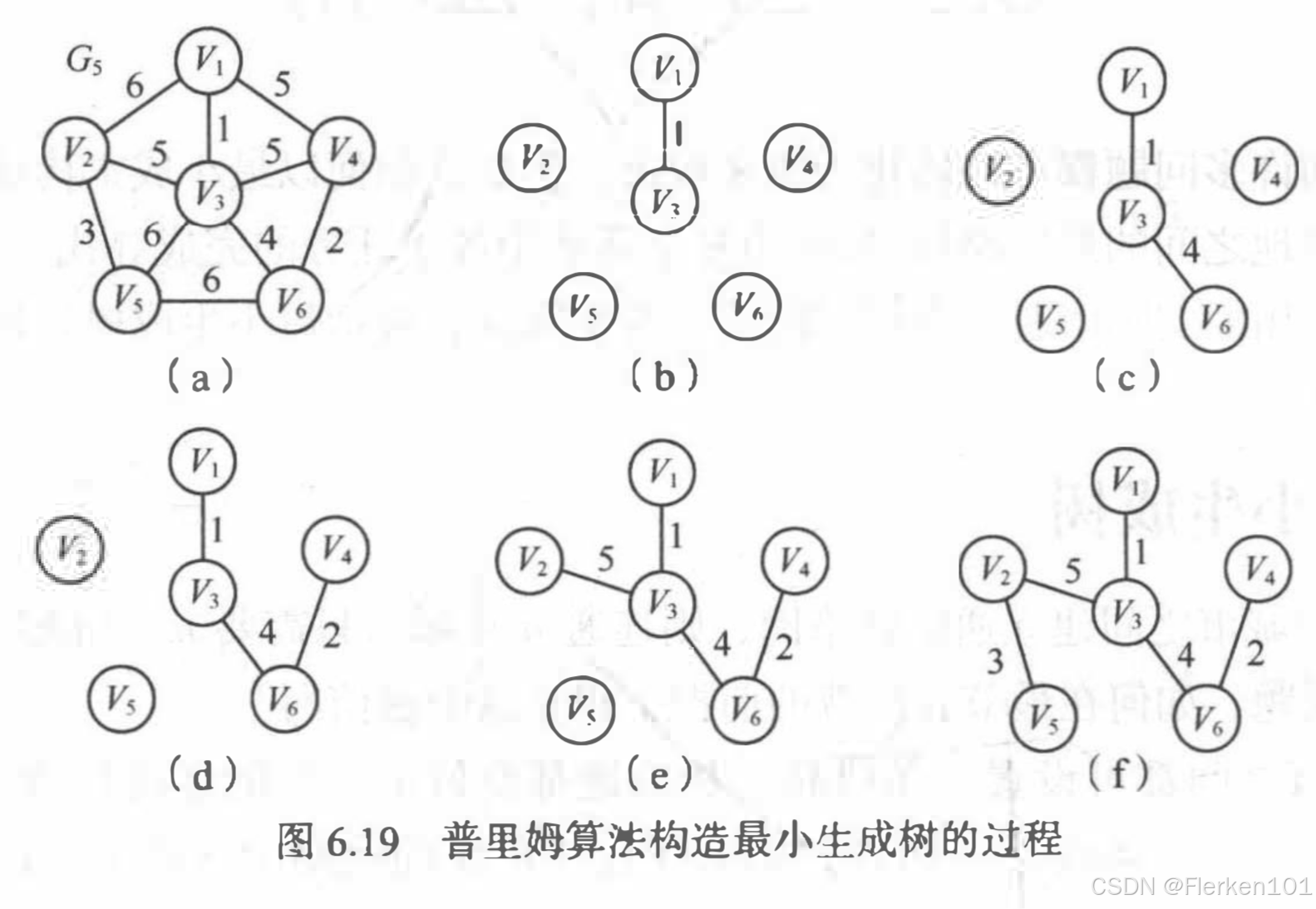
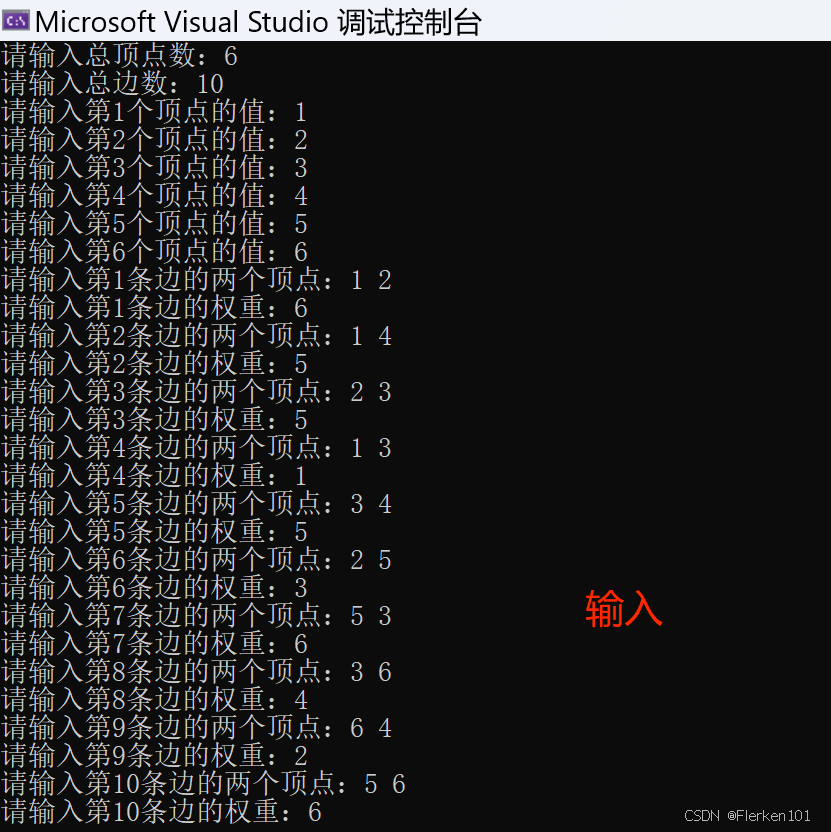
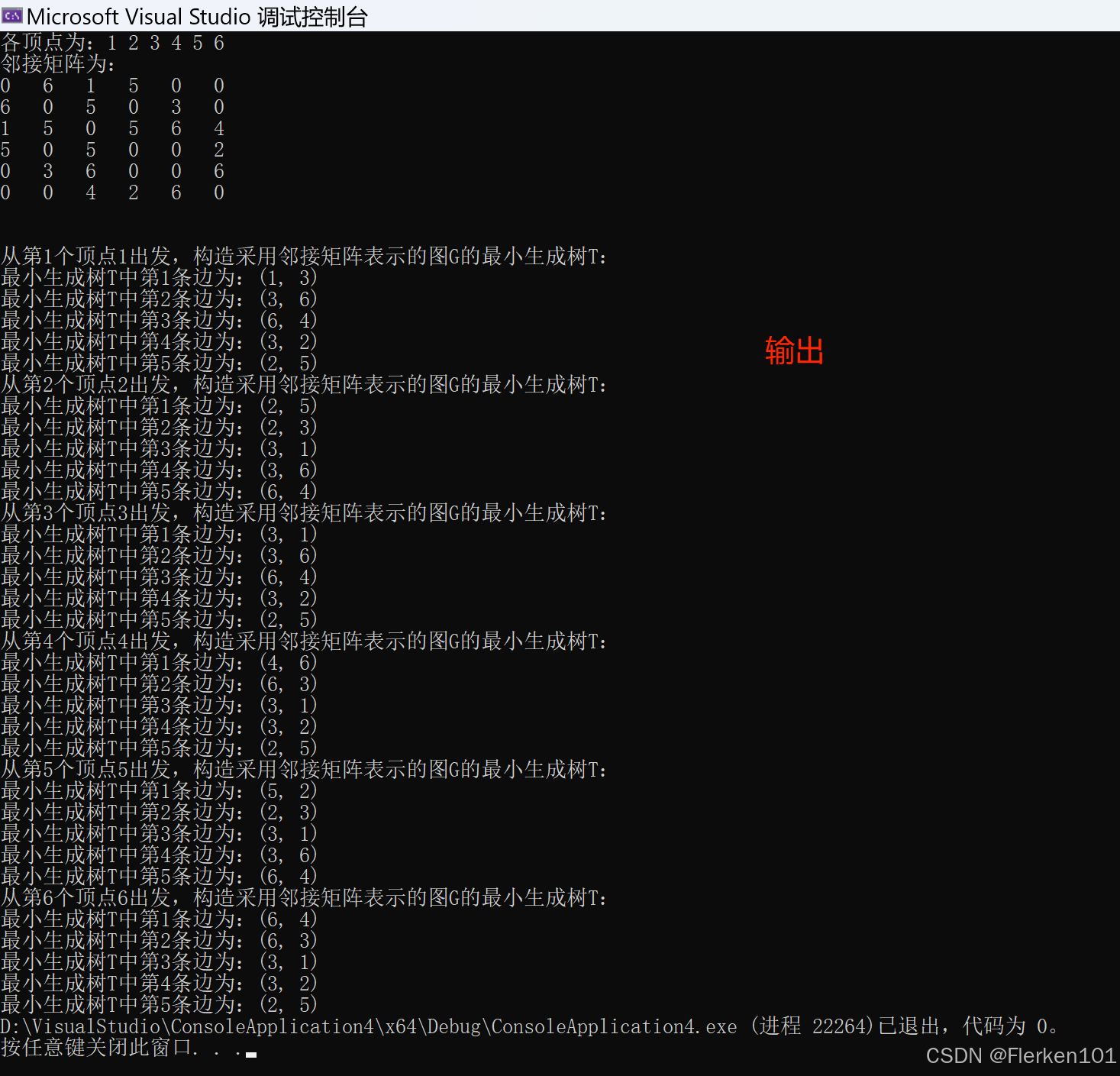
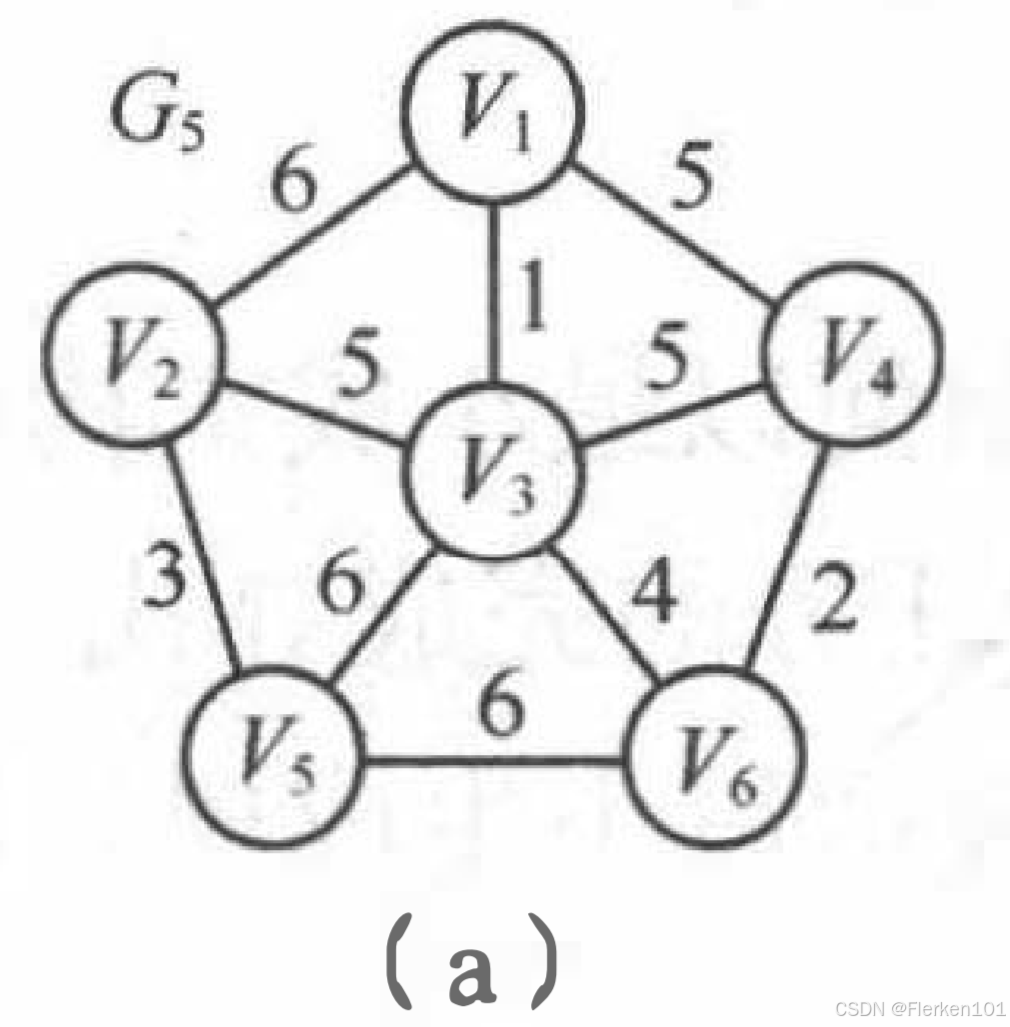
6.6.1.1普里姆算法(稠密网)
#include <stdio.h>
#include <stdlib.h>
#define MaxInt 32767
//此程序中,将无向网中的权值初始化了为0.因此最终不存在的边其权值为0,而非MaxInt
#define MVNum 100
typedef char VerTexType;
typedef int ArcType;
typedef struct AMGraph
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum;
int arcnum;
}AMGraph;
typedef struct V_UVexNode
{
VerTexType adjvex;
ArcType lowcost;
}V_UVexNode;
V_UVexNode closedge[MVNum]; //此声明数组中前面不能加typedef
void CreateAMGraph(AMGraph& G);
int LocateVex(AMGraph G, VerTexType e);
void printAMGraph(AMGraph G);
void MiniSpanTree_Prim(AMGraph G, VerTexType u);
int Min(AMGraph G, V_UVexNode closedge[]);
int main()
{
AMGraph G = { {0},{0},0,0 };
int i = 0;
CreateAMGraph(G);
printAMGraph(G);
printf("\n");
for (i = 0; i < G.vexnum; i++)
{
printf("\n从第%d个顶点%c出发,构造采用邻接矩阵表示的图G的最小生成树T:", i + 1, G.vexs[i]);
MiniSpanTree_Prim(G, G.vexs[i]);
}
return 0;
}
//构造邻接矩阵
void CreateAMGraph(AMGraph& G)
{
printf("请输入总顶点数:");
scanf_s(" %d", &G.vexnum);
printf("请输入总边数:");
scanf_s(" %d", &G.arcnum);
int i = 0;
int j = 0;
int k = 0;
VerTexType v1 = '\0';
VerTexType v2 = '\0';
ArcType w = 0;
for (i = 0; i < G.vexnum; i++)
{
printf("请输入第%d个顶点的值:", i + 1);
scanf_s(" %c", &G.vexs[i], sizeof(VerTexType));
for (j = 0; j < G.vexnum; j++)
{
G.arcs[i][j] = 0;
}
}
for (k = 0; k < G.arcnum; k++)
{
printf("请输入第%d条边的两个顶点:", k + 1);
scanf_s(" %c %c", &v1, sizeof(VerTexType), &v2, sizeof(VerTexType));
printf("请输入第%d条边的权重:", k + 1);
scanf_s(" %d", &w, sizeof(ArcType));
i = LocateVex(G, v1);
j = LocateVex(G, v2);
G.arcs[i][j] = w;
G.arcs[j][i] = G.arcs[i][j];
}
}
int LocateVex(AMGraph G, VerTexType e)
{
int i = 0;
for (i = 0; i < G.vexnum && G.vexs[i] != e; i++)
{
;
}
return i;
}
void printAMGraph(AMGraph G)
{
int i = 0;
int j = 0;
printf("\n各顶点为:");
for (i = 0; i < G.vexnum; i++)
{
printf("%c ", G.vexs[i]);
}
printf("\n邻接矩阵为:\n");
for (i = 0; i < G.vexnum; i++)
{
for (j = 0; j < G.vexnum; j++)
{
if (G.arcs[i][j] == 0)
{
printf("%d ", G.arcs[i][j]);
}
else
{
printf("%d ", G.arcs[i][j]);
}
}
printf("\n");
}
}
//无向网G以邻接矩阵形式存储,从顶点u出发构造G的最小生成树T, 输出T的各条边
void MiniSpanTree_Prim(AMGraph G, VerTexType u)
{
int k = 0;
int i = 0;
int j = 0;
VerTexType u0 = '\0';
VerTexType v0 = '\0';
k = LocateVex(G, u);
for (j = 0; j < G.vexnum; ++j)
{
if (j != k && (G.arcs[k][j] != 0))
// G.arcs[k][j] != 0代表各顶点与起始顶点u之间的边存在时,再将其权值存储到closedge数组中
{
closedge[j].adjvex = u;
closedge[j].lowcost = G.arcs[k][j];
}
else if (j == k) //如果是第k+1个顶点,起始顶点u本身,则将其在closedge数组中相应位置的closedge[k].adjvex置为$
{
closedge[k].adjvex = '$';
closedge[k].lowcost = 0;
}
else if(G.arcs[k][j] == 0) //如果各顶点Vj+1与第k+1个顶点,起始顶点u之间的边不存在,则将closedge数组中的closedge[j].adjvex置为#
{
closedge[j].adjvex = '#';
closedge[k].lowcost = 0;
}
}
for (i = 1; i < G.vexnum; ++i)
{
k = Min(G, closedge); //closedge数组中各顶点的下标与G.vexs中各顶点的下标是一一对应的
u0 = closedge[k].adjvex;
v0 = G.vexs[k]; //closedge数组中各顶点的下标与G.vexs中各顶点的下标是一一对应的
printf("\n最小生成树T中第%d条边为:(%c, %c)", i, u0, v0);
closedge[k].adjvex = '$';
closedge[k].lowcost = 0;
for (j = 0; j < G.vexnum; ++j)
{
if ((G.arcs[k][j] != 0) && (closedge[j].adjvex != '$') && (G.arcs[k][j] < closedge[j].lowcost))
//Vk+1在顶点集U中(closedge[k].adjvex 为 '$'),Vj+1还在顶点集V-U中时(closedge[j].adjvex != '$'),且(Vk+1,Vj+1)这条边存在(G.arcs[k][j] != 0), 再将G.arcs[k][j] 和 closedge[j].lowcost相比较
{
closedge[j].adjvex = G.vexs[k];
closedge[j].lowcost = G.arcs[k][j];
}
else if ((closedge[j].adjvex == '#') && (G.arcs[k][j] != 0))
//顶点U中之前所有的顶点都与Vj+1之间不存在边,现在新加入Vk+1与Vj+1之间存在了边,则不用比较权值(closedge[j].lowcost一定为0),直接将将其权值G.arcs[k][j]存入closedge[j].lowcost
{
closedge[j].adjvex = G.vexs[k];
closedge[j].lowcost = G.arcs[k][j];
}
}
}
}
int Min(AMGraph G, V_UVexNode closedge[])
{
int i = 0;
int j = 0;
int k = 0;
while (closedge[i].lowcost == 0)
{
i++;
}
//找到V-U中的第一个顶点,跳出
VerTexType minAdjvex = closedge[i].adjvex;
ArcType minCost = closedge[i].lowcost;
j = i;
/* 谨记此处要记录一下j = i !!! 因为如果整个程序,至运行结束一次也不进入for循环中的if语句的话,
那么此时的closedge[i].lowcost就是closedge数组中最小的权值,也要用j返回 */
for (k = i + 1; k < G.vexnum; k++)
{
if (closedge[k].lowcost != 0 && minCost > closedge[k].lowcost)
{
minAdjvex = closedge[k].adjvex;
minCost = closedge[k].lowcost;
j = k;
}
}
return j;
}
//无向网G以邻接矩阵形式存储,从顶点u出发构造G的最小生成树T, 输出T的各条边
void MiniSpanTree_Prim(AMGraph G, VerTexType u)
{
int k = 0;
int i = 0;
int j = 0;
VerTexType u0 = '\0';
VerTexType v0 = '\0';
printf("\nu = %c", u);
k = LocateVex(G, u);
printf("\nk = %d", k);
for (j = 0; j < G.vexnum; ++j)
{
if (j != k && (G.arcs[k][j] != 0))
// G.arcs[k][j] != 0代表各顶点与起始顶点u之间的边存在时,再将其权值存储到closedge数组中
{
closedge[j].adjvex = u;
closedge[j].lowcost = G.arcs[k][j];
}
else if (j == k) //如果是第k+1个顶点,起始顶点u本身,则将其在closedge数组中相应位置的closedge[k].adjvex置为$
{
closedge[k].adjvex = '$';
closedge[k].lowcost = 0;
}
else if(G.arcs[k][j] == 0) //如果各顶点Vj+1与第k+1个顶点,起始顶点u之间的边不存在,则将closedge数组中的closedge[j].adjvex置为#
{
closedge[j].adjvex = '#';
closedge[k].lowcost = 0;
}
}
//打印初始化后的closedge数组
printf("\n\n打印初始化后的closedge数组:");
for (i = 0; i < G.vexnum; i++)
{
printf("\nclosedge[%d].adjvex = %c", i, closedge[i].adjvex);
printf(", closedge[%d].lowcost = %d", i, closedge[i].lowcost);
}
for (i = 1; i < G.vexnum; ++i)
{
k = Min(G, closedge); //closedge数组中各顶点的下标与G.vexs中各顶点的下标是一一对应的
printf("\n\n第%d次for循环:k = %d", i, k);
u0 = closedge[k].adjvex;
printf("\n第%d次for循环:u0 = %c", i, u0);
v0 = G.vexs[k]; //closedge数组中各顶点的下标与G.vexs中各顶点的下标是一一对应的
printf("\n第%d次for循环:v0 = %c", i, v0);
printf("\n最小生成树T中第%d条边为:(%c, %c)", i, u0, v0);
closedge[k].adjvex = '$';
closedge[k].lowcost = 0;
printf("\n第%d次for循环往U中新加的顶点为: %c", i, G.vexs[k]);
for (j = 0; j < G.vexnum; ++j)
{
if ((G.arcs[k][j] != 0) && (closedge[j].adjvex != '$') && (G.arcs[k][j] < closedge[j].lowcost))
//Vk+1在顶点集U中(closedge[k].adjvex 为 '$'),Vj+1还在顶点集V-U中时(closedge[j].adjvex != '$'),且(Vk+1,Vj+1)这条边存在(G.arcs[k][j] != 0), 再将G.arcs[k][j] 和 closedge[j].lowcost相比较
{
printf("\n更新的closedge数组的下标为:%d", j);
closedge[j].adjvex = G.vexs[k];
closedge[j].lowcost = G.arcs[k][j];
printf("\nclosedge[%d].adjvex = %c", j, closedge[j].adjvex);
printf(", closedge[%d].lowcost = %d", j, closedge[j].lowcost);
}
else if ((closedge[j].adjvex == '#') && (G.arcs[k][j] != 0))
{
closedge[j].adjvex = G.vexs[k];
closedge[j].lowcost = G.arcs[k][j];
}
}
printf("\n打印第%d次for循环更新后的closedge数组:", i);
for (j = 0; j < G.vexnum; j++) //不能用i作为下标了,退出for循环后,i的值会被延续
{
printf("\nclosedge[%d].adjvex = %c", j, closedge[j].adjvex);
printf(", closedge[%d].lowcost = %d", j, closedge[j].lowcost);
}
}
}
int Min(AMGraph G, V_UVexNode closedge[])
{
int i = 0;
int j = 0;
int k = 0;
while (closedge[i].lowcost == 0)
{
i++;
}
//找到V-U中的第一个顶点,跳出
VerTexType minAdjvex = closedge[i].adjvex;
ArcType minCost = closedge[i].lowcost;
j = i;
/* 谨记此处要记录一下j = i !!! 因为如果整个程序,至运行结束一次也不进入for循环中的if语句的话,
那么此时的closedge[i].lowcost就是closedge数组中最小的权值,也要用j返回 */
printf("\nminAdjvex = closedge[%d].adjvex = %c", i, closedge[i].adjvex);
printf("\nminCost = closedge[%d].lowcost = %d", i, closedge[i].lowcost);
for (k = i + 1; k < G.vexnum; k++)
{
printf("\nk = %d", k);
if (closedge[k].lowcost != 0 && minCost > closedge[k].lowcost)
{
minAdjvex = closedge[k].adjvex;
minCost = closedge[k].lowcost;
printf("\nif条件中:k = %d", k);
j = k;
printf("\nif条件中:j = %d", j);
}
}
printf("\nj = %d", j);
return j;
}
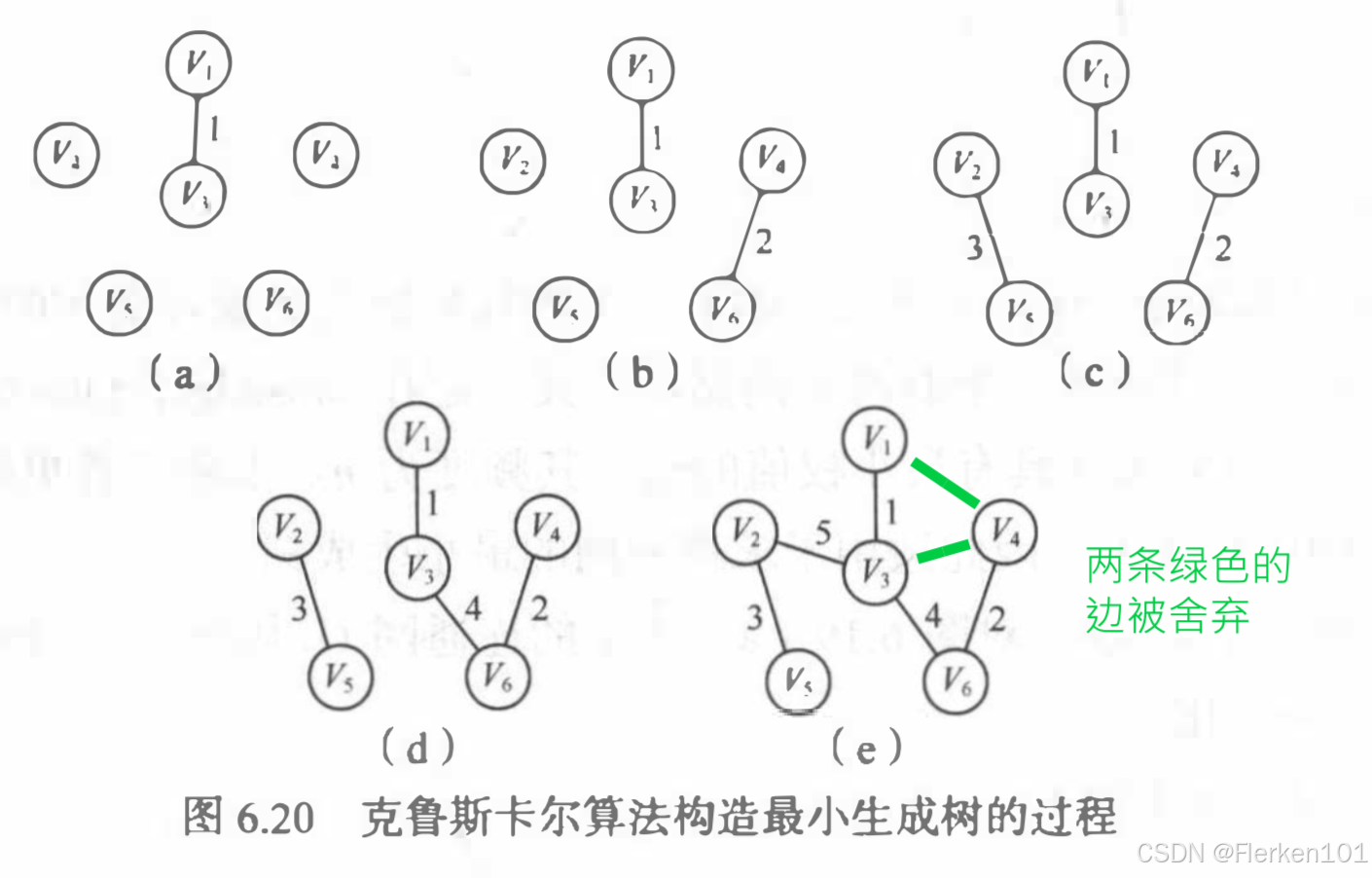
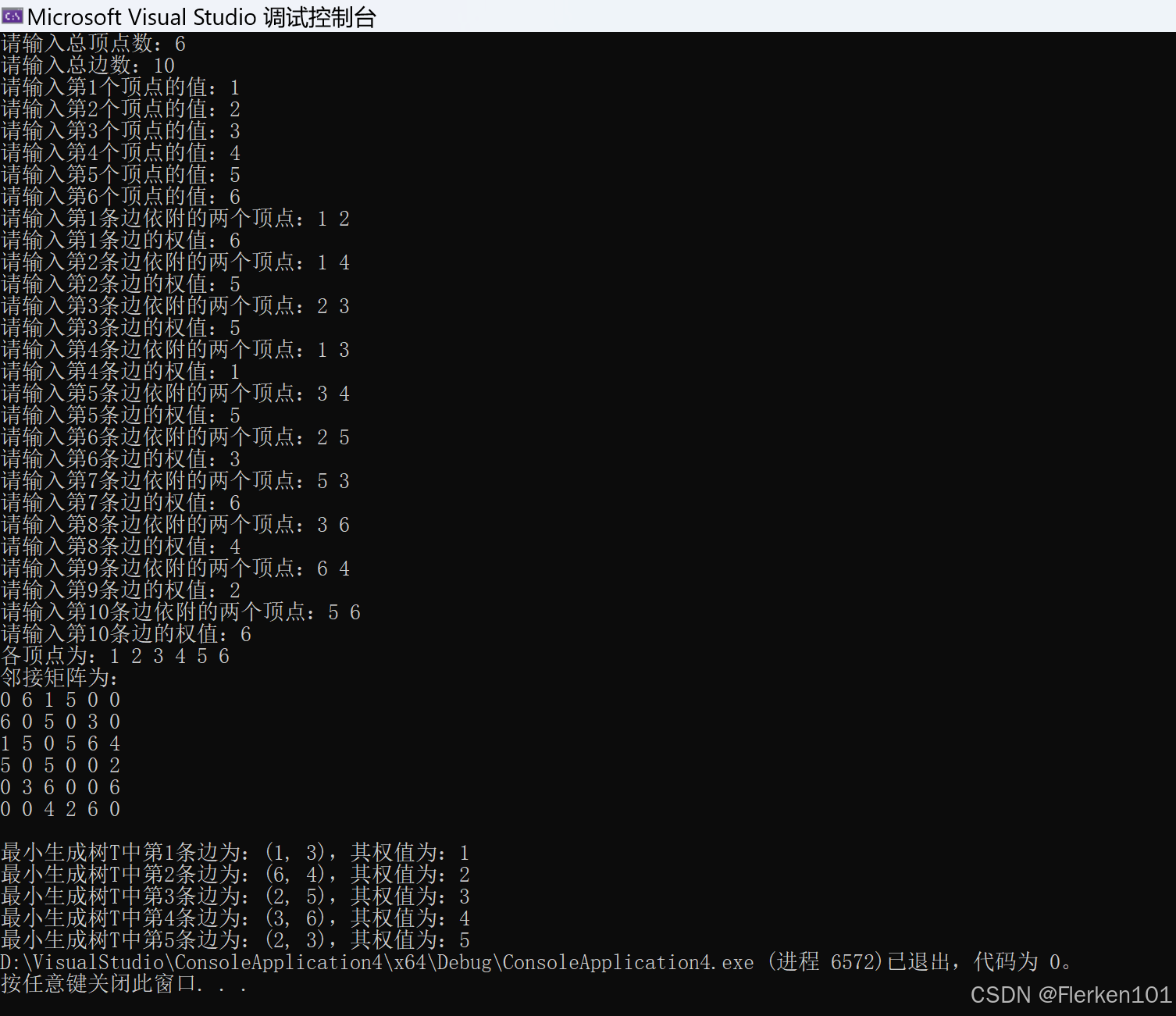
6.6.1.2克鲁斯卡尔算法(稀疏网)
#include <stdio.h>
#include <stdlib.h>
#define MVNum 100
#define MANum 200
typedef char VerTexType;
typedef int ArcType;
typedef struct
{
VerTexType vexs[MVNum];
ArcType arcs[MVNum][MVNum];
int vexnum;
int arcnum;
}AMGraph;
//辅助数组Edge的定义
typedef struct arc
{
VerTexType Head;
VerTexType Tail;
ArcType lowcost;
}arc;
arc Edge[MANum];
//辅助数组Vexset的定义
int Vexset[MVNum];
void CreateAMGraph(AMGraph& G);
int LocateVex(AMGraph G, VerTexType v);
void printAMGraph(AMGraph G);
void MinSpanTree_Kruskal(AMGraph G);
void Quick_Sort(arc Edge[], int low, int high);
int main()
{
AMGraph G = { {0},{0},0,0 };
CreateAMGraph(G);
printAMGraph(G);
MinSpanTree_Kruskal(G);
return 0;
}
void CreateAMGraph(AMGraph& G)
{
printf("请输入总顶点数:");
scanf_s(" %d", &G.vexnum);
printf("请输入总边数:");
scanf_s(" %d", &G.arcnum);
int i = 0;
int j = 0;
int k = 0;
VerTexType v1 = '\0';
VerTexType v2 = '\0';
ArcType w = 0;
for (i = 0; i < G.vexnum; i++)
{
printf("请输入第%d个顶点的值:", i + 1);
scanf_s(" %c", &G.vexs[i]);
for (j = 0; j < G.vexnum; j++)
{
G.arcs[i][j] = 0;
}
}
for (k = 0; k < G.arcnum; k++)
{
printf("请输入第%d条边依附的两个顶点:", k + 1);
scanf_s(" %c %c", &v1, sizeof(VerTexType), &v2, sizeof(VerTexType));
printf("请输入第%d条边的权值:",k+1);
scanf_s(" %d", &w);
Edge[k].Head = v1;
Edge[k].Tail = v2;
Edge[k].lowcost = w;
i = LocateVex(G, v1);
j = LocateVex(G, v2);
G.arcs[i][j] = w;
G.arcs[j][i] = G.arcs[i][j];
}
}
int LocateVex(AMGraph G, VerTexType v)
{
int i = 0;
for (i = 0; i < G.vexnum && G.vexs[i] != v; i++)
{
;
}
return i;
}
void printAMGraph(AMGraph G)
{
int i = 0;
int j = 0;
printf("各顶点为:");
for (i = 0; i < G.vexnum; i++)
{
printf("%c ", G.vexs[i]);
}
printf("\n邻接矩阵为:\n");
for (i = 0; i < G.vexnum; i++)
{
for (j = 0; j < G.vexnum; j++)
{
printf("%d ", G.arcs[i][j]);
}
printf("\n");
}
}
//无向网G以邻接矩阵形式存储,构造G的最小生成树T, 输出T的各条边
void MinSpanTree_Kruskal(AMGraph G)
{
int i = 0;
int j = 0;
int v1 = '\0';
int v2 = '\0';
int vs1 = 0;
int vs2 = 0;
int edgeCount = 0; //记录已加入MST的边数
Quick_Sort(Edge,0,G.arcnum -1);
/* Vexset数组与G.vexs数组中的下标是一一对应的,即图中被标记序号为第i+1个的顶点Vi,其在G.vexs数组中的下标是i.
那么在Vexset数组中,下标为i处,存储的就是第i+1个的顶点Vi所在的连通分量的信息。*/
for (i = 0; i < G.vexnum; i++)
{
Vexset[i] = i;
}
//每个连通分量用序号来命名。Vexset数组中各下标i处的值i,代表的就是图中第i+1个的顶点Vi所在的连通分量。
for (i = 0; i < G.arcnum; i++)
{
v1 = LocateVex(G, Edge[i].Head);
v2 = LocateVex(G, Edge[i].Tail);
vs1 = Vexset[v1];
vs2 = Vexset[v2];
if (vs1 != vs2)
{
edgeCount++;
printf("\n最小生成树T中第%d条边为:(%c, %c),其权值为:%d", edgeCount,Edge[i].Head, Edge[i].Tail,Edge[i].lowcost);
for (j = 0; j < G.vexnum; ++j)
{
if (Vexset[j] == vs2)
{
Vexset[j] = vs1;
}
}
}
}
}
//运用快速排序法
void Quick_Sort(arc Edge[], int low,int high)
{
int i = low;
int j = high;
arc key_arc = Edge[i];
int key = Edge[i].lowcost;
while (i < j)
{
while (i < j && Edge[j].lowcost >= key)
{
j--;
}
Edge[i] = Edge[j];
while (i < j && Edge[i].lowcost <= key)
{
i++;
}
Edge[j] = Edge[i];
}
Edge[i] = key_arc;
if (i - 1 > low)
{
Quick_Sort(Edge, low, i - 1);
}
if (i + 1 < high)
{
Quick_Sort(Edge, i+1, high);
}
}
//无向网G以邻接矩阵形式存储,构造G的最小生成树T, 输出T的各条边
void MinSpanTree_Kruskal(AMGraph G)
{
int i = 0;
int j = 0;
int v1 = '\0';
int v2 = '\0';
int vs1 = 0;
int vs2 = 0;
int edgeCount = 0; //记录已加入MST的边数
printf("\n排序之前Edge数组中的各边顺序为:");
for (i = 0; i < G.arcnum; i++)
{
printf("\n Edge[%d] :(%c, %c),其权值为:%d",i, Edge[i].Head, Edge[i].Tail, Edge[i].lowcost);
}
Quick_Sort(Edge,0,G.arcnum -1);
printf("\n\n排序之后Edge数组中的各边顺序为:");
for (i = 0; i < G.arcnum; i++)
{
printf("\n Edge[%d] :(%c, %c),其权值为:%d", i, Edge[i].Head, Edge[i].Tail, Edge[i].lowcost);
}
/* Vexset数组与G.vexs数组中的下标是一一对应的,即图中被标记序号为第i+1个的顶点Vi,其在G.vexs数组中的下标是i.
那么在Vexset数组中,下标为i处,存储的就是第i+1个的顶点Vi所在的连通分量的信息。*/
for (i = 0; i < G.vexnum; i++)
{
Vexset[i] = i;
}
//每个连通分量用序号来命名。Vexset数组中各下标i处的值i,代表的就是图中第i+1个的顶点Vi所在的连通分量。
printf("\n打印初始化后的辅助数组Vexset:");
for (i = 0; i < G.vexnum; i++)
{
printf("\nVexset[%d] = %d", i, Vexset[i]);
}
for (i = 0; i < G.arcnum; i++)
{
printf("\n\n正在进行判断的边是:(%c, %c),其权值为:%d", Edge[i].Head, Edge[i].Tail, Edge[i].lowcost);
v1 = LocateVex(G, Edge[i].Head);
v2 = LocateVex(G, Edge[i].Tail);
vs1 = Vexset[v1];
printf("\n顶点%c所属连通分量的下标为:%d", Edge[i].Head, vs1);
vs2 = Vexset[v2];
printf("\n顶点%c所属连通分量的下标为:%d", Edge[i].Tail, vs2);
if (vs1 != vs2)
{
edgeCount++;
printf("\n最小生成树T中第%d条边为:(%c, %c),其权值为:%d", edgeCount,Edge[i].Head, Edge[i].Tail,Edge[i].lowcost);
for (j = 0; j < G.vexnum; ++j)
{
if (Vexset[j] == vs2)
{
Vexset[j] = vs1;
}
}
printf("\n打印更新后的辅助数组Vexset:");
for (j = 0; j < G.vexnum; j++)
//不能用i做下标值,结束该for循环后,i值还会延续
{
printf("\nVexset[%d] = %d", j, Vexset[j]);
}
}
}
}