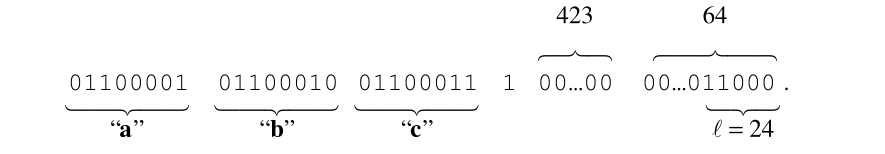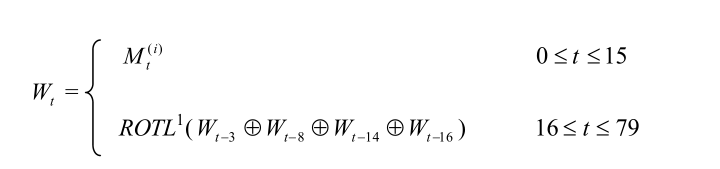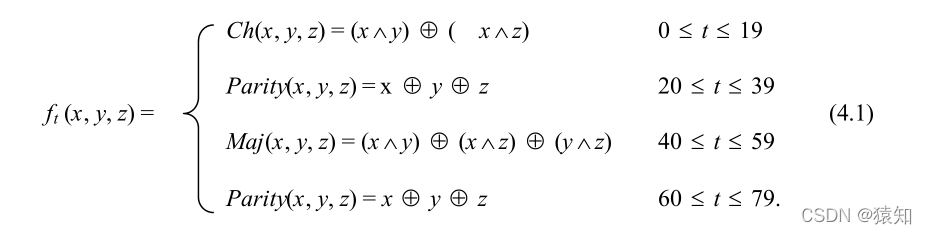系列索引:【图解安全加密算法】加密算法系列索引 Python保姆级实现教程 | 物联网安全 | 信息安全
起初写实验时找到的代码大多基于c/c++,python可参考的资料很少,所以借着这次实验的机会把自己走过坑分享一下,希望对大家有所帮助!
一、什么是SHA1
SHA-1是一种数据加密算法,该算法的思维是接纳一段明文,然后以一种不可逆的方式将它转换成一段(一般更小)密文,也能够简略的理解为取一串输入码(称为预映射或信息),并把它们转化为长度较短、位数固定的输出序列即散列值(也称为摘要信息或信息认证代码)的过程
二、SHA1哈希算法流程
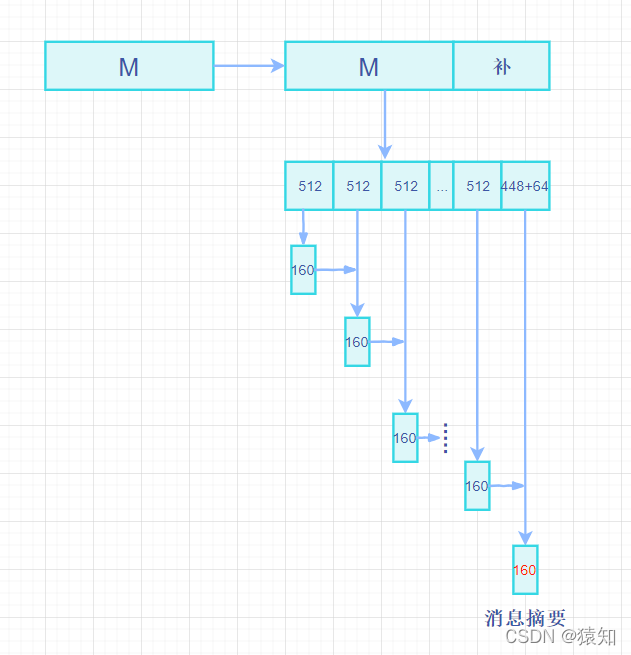
对于任意长度的明文,SHA1首先对其进行分组,使得每一组的长度为512位,然后对这些明文分组反复重复处理。
每个明文分组的摘要生成过程如下:
(1) 将512位的明文分组划分为16个子明文分组,每个子明文分组为32位。
(2) 申请5个32位的链接变量,记为A、B、C、D、E。
(3) 16份子明文分组扩展为80份。
(4) 80份子明文分组进行4轮运算。
(5) 链接变量与初始链接变量进行求和运算。
(6) 链接变量作为下一个明文分组的输入重复进行以上操作。
(7) 最后,5个链接变量里面的数据就是SHA1摘要。
三、具体实现过程(附代码)
在进行散列值计算之前,先要对需要加密的数据进行预处理。这一预处理由三部分组成:消息填充、分割已填充消息(将填充后的消息等分成m位处理块)、为散列值计算设置初始化值。
(1)消息填充
假设原始消息(M)的长度是L位。首先,在消息最后加一位“1”,接着在这位“1”后面补k个“0”,使得L+1+k(即补位后的消息长度)满足对512取模后余数是448。然后,添加最后的64位二进制数据,这64位二进制数据就是原始L位消息(M)长度的二进制表示。
flag = 1 # 补1标志位,补一次1后置0
while len(M) % 512 != 448: #M是未补位的二进制串(字符串类型)
if flag:
M += '1'
flag = 0
else:
M += '0'
M += "{:064b}".format(l) # 末尾64位写入长度,空余补位补0
M = hex(int(M, 2))[2:] # 这种转换会用到很多次,2进制转16进制,M现在是一个16进制字符串,如'1342a2c12...'
补位后如下:
(2)分割已填充消息
经过消息填充后,还必须将数据划分成m位一组的N块的数据块来提供给下面的散列值计算过程。对于SHA-1加密算法,填充过的消息被分割成N(M(1),M(2),…,M(N))块,每块512位。(其长度正好为512位的整数倍,然后按512位的长度进行分组(block))然后每组512位的输入块可以表示成16个32位的字,分别记为:M0(i),M1(i),…,M15(i)。
Mn = [] # 存储每个32位的字,因为M中一个字符4位(16进制),
#所以取M中的8个为一组,按要求将M分割成16个32位的字,故这里8*4=32,32*16=512
for i in range(16):
Mn.append(M[8*i: 8*i+8])
(3)设置初始散列值
初始散列值由下面5个32位的字组成,其16进制表示如下:
A=0x67452301,B=0xEFCDAB89,C=0x98BADCFE,D=0x10325476,E=0xC3D2E1F0。
(4)16份子明文分组扩展为80份
将这16份子明文分组扩充到80份子明文分组,我们记为W[k](k= 0, 1,……79),扩充的方法如下。
Wt = Mt , 当0≤t≤15
Wt = (Wt-3⊕Wt-8⊕ Wt-14⊕Wt-16) <<< 1, 当16≤t≤79
W = ['' for _ in range(80)] # 存储80份扩展子明文
for i in range(80):
if 16 <= i <= 79:
# 16-79要进行异或运算,这里先转换成十进制(W中存的是16进制字符串,str无法运算)
temp = int(W[i-3], 16) ^ int(W[i-8],
16) ^ int(W[i-14], 16) ^ int(W[i-16], 16)
W[i] = hex(roll_left(temp, 1))[2:].zfill(8) # 循环左移1位
else:
W[i] = Mn[i]
(5)SHA1的4轮运算
SHA1有4轮运算,每一轮包括20个步骤,一共80步(对应扩展后的80个W[t]),当第1轮运算中的第1步骤开始处理时,A、B、C、D、E五个链接变量中的值先赋值到另外5个记录单元A′,B′,C′,D′,E′中。这5个值将保留,用于在第4轮的最后一个步骤完成之后与链接变量A,B,C,D,E进行求和操作。
SHA1的4轮运算,共80个步骤使用同一个操作程序,如下:
A,B,C,D,E←[(A<<<5)+ ft(B,C,D)+E+Wt+Kt],A,(B<<<30),C,D
其中 ft(B,C,D)为逻辑函数,Wt为子明文分组W[t],Kt为固定常数。
这个操作程序的意义为:
● 将[(A<<<5)+ ft(B,C,D)+E+Wt+Kt]的结果赋值给链接变量A;
● 将链接变量A初始值赋值给链接变量B;
● 将链接变量B初始值循环左移30位赋值给链接变量C;
● 将链接变量C初始值赋值给链接变量D;
● 将链接变量D初始值赋值给链接变量E。
Ap, Bp, Cp, Dp, Ep = A, B, C, D, E # 暂存初始值
for t in range(80):
tmp = B
B = A
A = ((((E + ft(tmp, C, D, t)) % (2**32)+roll_left(A, 5)) %
(2**32)+int(W[t], 16)) % (2**32)+K[t//20]) % (2**32) # 预防溢出进行取模运算
E = D
D = C
C = roll_left(tmp, 30)
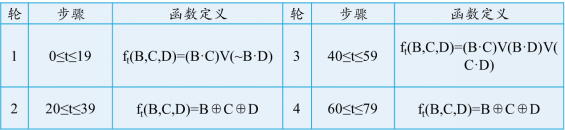
SHA1规定4轮运算的逻辑函数如表
def ft(b, c, d, t):
"""ft为逻辑函数
Parameters
----------
b : int
B值
c : int
C值
d : int
D值
t : int
轮次
Returns
-------
int
运算结果
"""
if t >= 0 and t <= 19:
return ((b & c) | (~b & d))
elif t >= 20 and t <= 39:
return (b ^ c ^ d)
elif t >= 40 and t <= 59:
return ((b & c) | (b & d) | (d & c))
elif t >= 60 and t <= 79:
return (b ^ c ^ d)
SHA1的常数K取值表
四、跟着demo去debug
这里使用’abc’进行测试,包括各个步骤的结果,供大家debug使用
这里将最后一轮(79轮)的结果与初始值相加。
五、完整代码
代码已补充,不足之处大佬见谅,还有很对待完善之处,欢迎大家批评指正!
import random
A, B, C, D, E = 0x67452301, 0xEFCDAB89, 0x98BADCFE, 0x10325476, 0xC3D2E1F0 # 常量
K = [0x5A827999, 0x6ED9EBA1, 0x8F1BBCDC, 0xCA62C1D6] # 常量
str = input("输入明文:\n").encode('utf-8') # 这里对输入明文进行编码,str为bytes型
l = len(str)*8 # 每个字符8位
# python中二进制是字符串,不保留高位的0,这里使用zfill补高位0,如十进制6->110->0110,M这里是用了一个很长的字符串如:'11001010100011...'来表示原始数据
M = bin(int(str.hex(), 16))[2:].zfill(l)
# [可选项] 下面的函数仅仅显示输入明文的ascii,末尾为长度,该段显示的是补位后的
for i in range(64):
if i < len(str):
print(str[i], end=' ')
elif i < len(str)+1:
print('128', end=' ')
elif i < 63:
print('0', end=' ')
else:
print(l)
flag = 1 # 补1标志位,补一次1后置0
while len(M) % 512 != 448:
if flag:
M += '1'
flag = 0
else:
M += '0'
M += "{:064b}".format(l) # 末尾64位写入长度,空余补位补0
M = hex(int(M, 2))[2:] # 这种转换会用到很多次,2进制转16进制,M现在是一个16进制字符串,如'1342a2c12...'
Mn = [] # 存储每个32位的字,因为M中一个字符4位(16进制),所以取M中的8个为一组,按要求将M分割成16个32位的字,故这里8*4=32,32*16=512
for i in range(16):
Mn.append(M[8*i: 8*i+8])
def roll_left(num, k):
"""循环左移函数
Parameters
----------
num : int
输入一个数字,2进制、10进制等均可
k : int
左移位数
Returns
-------
int
返回一个int结果
"""
num_bin = bin(num)[2:].zfill(
32) # 因为python高位不会自动补0,导致要手动调整(也可能是我学艺不精),不然会忽略高位的0循环左移
out = num_bin[k % len(num_bin):]+num_bin[:k % len(num_bin)] # 注意预防溢出
return int(out, 2) # 二进制左移完成后转化成10进制输出
W = ['' for _ in range(80)] # 存储80份扩展子明文
for i in range(80):
if 16 <= i <= 79:
# 16-79要进行异或运算,这里先转换成十进制(W中存的是16进制字符串,str无法运算)
temp = int(W[i-3], 16) ^ int(W[i-8],
16) ^ int(W[i-14], 16) ^ int(W[i-16], 16)
W[i] = hex(roll_left(temp, 1))[2:].zfill(8) # 循环左移1位
else:
W[i] = Mn[i]
def ft(b, c, d, t):
"""ft为逻辑函数
Parameters
----------
b : int
B值
c : int
C值
d : int
D值
t : int
轮次
Returns
-------
int
运算结果
"""
if t >= 0 and t <= 19:
return ((b & c) | (~b & d))
elif t >= 20 and t <= 39:
return (b ^ c ^ d)
elif t >= 40 and t <= 59:
return ((b & c) | (b & d) | (d & c))
elif t >= 60 and t <= 79:
return (b ^ c ^ d)
Ap, Bp, Cp, Dp, Ep = A, B, C, D, E # 暂存初始值
for t in range(80):
tmp = B
B = A
A = ((((E + ft(tmp, C, D, t)) % (2**32)+roll_left(A, 5)) %
(2**32)+int(W[t], 16)) % (2**32)+K[t//20]) % (2**32) # 预防溢出进行取模运算
E = D
D = C
C = roll_left(tmp, 30)
#print(f" round{t+1} : {hex(A)} {hex(B)} {hex(C)} {hex(D)} {hex(E)}\n")
A, B, C, D, E = (Ap+A) % (2**32), (Bp+B) % (2**32), (Cp +
C) % (2**32), (Dp+D) % (2**32), (Ep+E) % (2**32)
# 相加运算,因为python不像c/c++可以使用unsigned char_32直接限制位数,因此要对位数进行限制
print("明文对应的杂凑码:\n", hex(A), hex(B), hex(C), hex(D), hex(E))
图解安全加密算法系列持续更新,欢迎
点赞收藏+关注
上一篇:【图解DSA数字签名算法】DSA签名算法的Python实现 | 物联网安全 | 信息安全
下一篇:【图解RSA加密算法】RSA非对称密码算法的Python实现保姆级教程 | 物联网安全 | 信息安全
本人水平有限,文章中不足之处欢迎下方👇评论区批评指正~如果感觉对你有帮助,点个赞👍 支持一下吧 ~
不定期分享 有趣、有料、有营养内容,欢迎 订阅关注 🤝 我的博客 ,期待在这与你相遇 ~