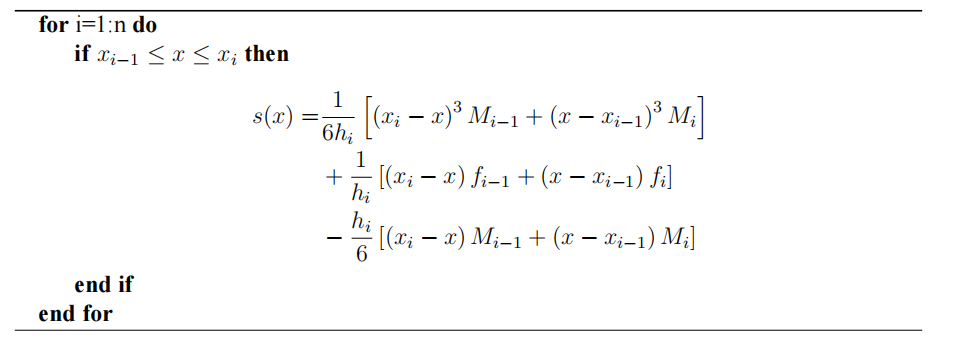文章对应视频讲解:(cubic spline)三次样条插值 Ⅰ、Ⅱ、Ⅲ 型
主要以实现为主,理论部分不做详细说明
一、三次样条插值
已知: s ( x i ) = f i , i = 1 , 2 , ⋯ , n − 1 s(x_i) = f_i, \quad i = 1,2,\cdots,n-1 s(xi)=fi,i=1,2,⋯,n−1 。
Ⅰ型边界条件: s ( x 0 ) = f 0 , s ( x n ) = f n s ′ ( x 0 ) = f 0 ′ , s ′ ( x n ) = f n ′ s(x_0) = f_0,s(x_n) = f_n \quad s'(x_0) = f'_0,s'(x_n)=f_n' s(x0)=f0,s(xn)=fns′(x0)=f0′,s′(xn)=fn′
Ⅱ型边界条件: s ( x 0 ) = f 0 , s ( x n ) = f n s ′ ′ ( x 0 ) = f 0 ′ ′ , s ′ ′ ( x n ) = f n ′ ′ s(x_0) = f_0,s(x_n) = f_n \quad s''(x_0) = f''_0,s''(x_n)=f''_n s(x0)=f0,s(xn)=fns′′(x0)=f0′′,s′′(xn)=fn′′
Ⅲ型边界条件: s ( x 0 ) = f 0 , s ( x n ) = s ( x 0 ) s ′ ( x 0 ) = s ′ ( x n ) , s ′ ′ ( x 0 ) = s ′ ′ ( x n ) s(x_0) = f_0,s(x_n) =s(x_0) \quad s'(x_0)=s'(x_n),s''(x_0)=s''(x_n) s(x0)=f0,s(xn)=s(x0)s′(x0)=s′(xn),s′′(x0)=s′′(xn)
设
h
i
=
x
i
−
x
i
−
1
,
e
i
h_i = x_{i}-x_{i-1} , e_i
hi=xi−xi−1,ei 为
[
x
i
−
1
,
x
i
]
[x_{i-1},x_i]
[xi−1,xi]构成的小区间,
i
=
1
,
2
,
⋯
,
n
i=1,2,\cdots,n
i=1,2,⋯,n
M
i
=
s
I
′
′
(
x
i
)
,
i
=
0
,
1
,
⋯
,
n
M_i = s''_I(x_i),i=0,1,\cdots,n
Mi=sI′′(xi),i=0,1,⋯,n
满足三次样条函数
s
(
x
)
s(x)
s(x)
s
(
x
)
=
1
6
h
i
[
(
x
i
−
x
)
3
M
i
−
1
+
(
x
−
x
i
−
1
)
3
M
i
]
+
1
h
i
[
(
x
i
−
x
)
f
i
−
1
+
(
x
−
x
i
−
1
)
f
i
]
−
h
i
6
[
(
x
i
−
x
)
M
i
−
1
+
(
x
−
x
i
−
1
)
M
i
]
\begin{aligned} s(x)=& \frac{1}{6h_i}\left[\left(x_i-x\right)^3M_{i-1}+\left(x-x_{i-1}\right)^3M_i\right] \\ &+\frac{1}{h_{i}}\left[\left(x_{i}-x\right)f_{i-1}+\left(x-x_{i-1}\right)f_{i}\right] \\ &-\frac{h_i}6\left[\left(x_i-x\right)M_{i-1}+\left(x-x_{i-1}\right)M_i\right] \end{aligned}
s(x)=6hi1[(xi−x)3Mi−1+(x−xi−1)3Mi]+hi1[(xi−x)fi−1+(x−xi−1)fi]−6hi[(xi−x)Mi−1+(x−xi−1)Mi]
其中
x
∈
e
i
,
i
=
1
,
2
,
⋯
,
n
x\in e_i,i=1,2,\cdots,n
x∈ei,i=1,2,⋯,n
λ
j
=
h
j
+
1
h
j
+
h
j
+
1
,
μ
j
=
1
−
λ
j
=
h
j
h
j
+
h
j
+
1
\lambda_j = \dfrac{h_{j+1}}{h_j+h_{j+1}},\mu_j=1-\lambda_j=\dfrac{h_{j}}{h_j+h_{j+1}}
λj=hj+hj+1hj+1,μj=1−λj=hj+hj+1hj
有
μ
j
M
j
−
1
+
2
M
j
+
λ
j
M
j
+
1
=
d
j
,
j
=
1
,
2
,
⋯
,
n
−
1
\begin{equation} \mu_jM_{j-1}+2M_j+\lambda_jM_{j+1}=d_j,\quad j=1,2,\cdots,n-1 \end{equation}
μjMj−1+2Mj+λjMj+1=dj,j=1,2,⋯,n−1
其中
d
j
=
6
f
[
x
j
−
1
,
x
j
,
x
j
+
1
]
d_j=6f\left[x_{j-1},x_j,x_{j+1}\right]
dj=6f[xj−1,xj,xj+1]
Ⅰ型边界条件下有:
{
2
M
0
+
M
1
=
6
h
1
(
f
1
−
f
0
h
1
−
f
0
′
)
:
=
d
0
M
n
−
1
+
2
M
n
=
6
h
n
(
f
n
′
−
f
n
−
f
n
−
1
h
n
)
:
=
d
n
\begin{equation} \begin{cases} 2M_0+M_1=\dfrac6{h_1}\left(\dfrac{f_1-f_0}{h_1}-f_0^{\prime}\right):=d_0\\ M_{n-1}+2M_n=\dfrac6{h_n}\left(f_n^{\prime}-\dfrac{f_n-f_{n-1}}{h_n}\right):=d_n \end{cases} \end{equation}
⎩
⎨
⎧2M0+M1=h16(h1f1−f0−f0′):=d0Mn−1+2Mn=hn6(fn′−hnfn−fn−1):=dn
联立(1)和(2),得线性方程组
[
2
1
μ
1
2
λ
1
μ
2
2
λ
2
⋱
⋱
⋱
μ
n
−
1
2
λ
n
−
1
1
2
]
[
M
0
M
1
M
2
⋮
M
n
−
1
M
n
]
=
[
d
0
d
1
d
2
⋮
d
n
−
1
d
n
]
\begin{equation} \begin{bmatrix}2&1\\\mu_1&2&\lambda_1\\&\mu_2&2&\lambda_2\\&&\ddots&\ddots&\ddots\\&&&\mu_{n-1}&2&\lambda_{n-1}\\&&&&1&2\end{bmatrix}\begin{bmatrix}M_0\\M_1\\M_2\\\vdots\\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_0\\d_1\\d_2\\\vdots\\d_{n-1}\\d_n\end{bmatrix} \end{equation}
2μ112μ2λ12⋱λ2⋱μn−1⋱21λn−12
M0M1M2⋮Mn−1Mn
=
d0d1d2⋮dn−1dn
Ⅱ 型边界条件下有:
M
0
=
f
0
′
′
,
M
n
=
f
n
′
′
\begin{equation} M_0=f_0^{\prime\prime},\quad M_n=f_n^{\prime\prime} \end{equation}
M0=f0′′,Mn=fn′′
联立(1)和(4),得线性方程组
[
1
μ
1
2
λ
1
μ
2
2
λ
2
⋱
⋱
⋱
μ
n
−
1
2
λ
n
−
1
1
]
[
M
0
M
1
M
2
⋮
M
n
−
1
M
n
]
=
[
f
0
′
′
d
1
d
2
⋮
d
n
−
1
f
n
′
′
]
\begin{equation} \begin{bmatrix}1&\\\mu_1&2&\lambda_1\\&\mu_2&2&\lambda_2\\&&\ddots&\ddots&\ddots\\&&&\mu_{n-1}&2&\lambda_{n-1}\\&&&&&1\end{bmatrix}\begin{bmatrix}M_0\\M_1\\M_2\\\vdots\\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}f_0^{\prime\prime}\\d_1\\d_2\\\vdots\\d_{n-1}\\f_n^{\prime\prime}\end{bmatrix} \end{equation}
1μ12μ2λ12⋱λ2⋱μn−1⋱2λn−11
M0M1M2⋮Mn−1Mn
=
f0′′d1d2⋮dn−1fn′′
进一步化简得 n-1阶三对角方程组
[
2
λ
1
μ
2
2
λ
2
⋱
⋱
⋱
μ
n
−
2
2
λ
n
−
2
μ
n
−
1
2
]
[
M
1
M
2
⋮
M
n
−
2
M
n
−
1
]
=
[
d
1
−
μ
1
f
0
′
′
d
2
⋮
d
n
−
2
d
n
−
1
−
λ
n
−
1
f
n
′
′
]
\begin{equation} \begin{bmatrix}2&\lambda_1\\\mu_2&2&\lambda_2\\&\ddots&\ddots&\ddots\\&&\mu_{n-2}&2&\lambda_{n-2}\\&&&\mu_{n-1}&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\\vdots\\M_{n-2}\\M_{n-1}\end{bmatrix}=\begin{bmatrix}d_1-\mu_1f''_0\\d_2\\\vdots\\d_{n-2}\\d_{n-1}-\lambda_{n-1}f''_n\end{bmatrix} \end{equation}
2μ2λ12⋱λ2⋱μn−2⋱2μn−1λn−22
M1M2⋮Mn−2Mn−1
=
d1−μ1f0′′d2⋮dn−2dn−1−λn−1fn′′
Ⅲ 型边界条件下有:
M
0
=
M
n
,
λ
n
M
1
+
μ
n
M
n
−
1
+
2
M
n
=
d
n
\begin{equation} M_0=M_n,\lambda_nM_1+\mu_nM_{n-1}+2M_n=d_n \end{equation}
M0=Mn,λnM1+μnMn−1+2Mn=dn
其中
λ
n
=
h
1
/
(
h
1
+
h
n
)
,
μ
n
=
h
n
/
(
h
1
+
h
n
)
d
n
=
6
(
f
[
x
0
,
x
1
]
−
f
[
x
n
−
1
,
x
n
]
)
/
(
h
1
+
h
n
)
\lambda_n=h_1/(h_1+h_{n}),\mu_n=h_{n}/(h_1+h_{n})\\\ \\d_n=6(f[x_0,x_1]-f[x_{n-1},x_n])/(h_1+h_{n})
λn=h1/(h1+hn),μn=hn/(h1+hn) dn=6(f[x0,x1]−f[xn−1,xn])/(h1+hn)
联立(1)和(7),得线性方程组
[
1
−
1
μ
1
2
λ
1
μ
2
2
λ
2
⋱
⋱
⋱
μ
n
−
1
2
λ
n
−
1
λ
n
μ
n
2
]
[
M
0
M
1
M
2
⋮
M
n
−
1
M
n
]
=
[
0
d
1
d
2
⋮
d
n
−
1
d
n
]
\begin{equation} \begin{bmatrix}1&&&&&-1\\\mu_1&2&\lambda_1\\&\mu_2&2&\lambda_2\\&&\ddots&\ddots&\ddots\\&&&\mu_{n-1}&2&\lambda_{n-1}\\ &\lambda_n&&&\mu_n&2\end{bmatrix}\begin{bmatrix}M_0\\M_1\\M_2\\\vdots\\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}0\\d_1\\d_2\\\vdots\\d_{n-1}\\d_n\end{bmatrix} \end{equation}
1μ12μ2λnλ12⋱λ2⋱μn−1⋱2μn−1λn−12
M0M1M2⋮Mn−1Mn
=
0d1d2⋮dn−1dn
进一步化简得 n阶线性方程组
[
2
λ
1
μ
1
μ
2
2
λ
2
⋱
⋱
⋱
μ
n
−
1
2
λ
n
−
1
λ
n
μ
n
2
]
[
M
1
M
2
⋮
M
n
−
1
M
n
]
=
[
d
1
d
2
⋮
d
n
−
1
d
n
]
\begin{equation} \begin{bmatrix}2&\lambda_1&&&\mu_1\\\mu_2&2&\lambda_2&&\\&\ddots&\ddots&\ddots&\\&&\mu_{n-1}&2&\lambda_{n-1}\\\lambda_n&&&\mu_n&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\\vdots\\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}d_1\\d_2\\\vdots\\d_{n-1}\\d_{n}\end{bmatrix} \end{equation}
2μ2λnλ12⋱λ2⋱μn−1⋱2μnμ1λn−12
M1M2⋮Mn−1Mn
=
d1d2⋮dn−1dn
最终,通过解线性方程组,可以得到
M
0
,
M
1
,
⋯
,
M
n
M_0,M_1,\cdots,M_n
M0,M1,⋯,Mn,代入到
s
(
x
)
s(x)
s(x)中,得三次样条插值函数
二、算法
对I型进行详细介绍, II,III型是类似的,不作详细说明
Ⅰ型三次样条插值
输入:
- n + 1 n+1 n+1 个插值节点 ( x i , y i ) , i = 0 , 1 , ⋯ , n (x_i,y_i),i=0,1,\cdots,n (xi,yi),i=0,1,⋯,n 构成向量 x 0 , y 0 x_0,y_0 x0,y0
- I型边界条件 f 0 ′ , f n ′ f'_0,f'_n f0′,fn′
- 目标近似点 x x x
输出
- 近似点的值 y y y
实现步骤
-
步骤 1 1 1: 计算 h i = x i − x i − 1 , i = 1 , 2 , ⋯ , n h_i = x_i-x_{i-1},i=1,2,\cdots,n hi=xi−xi−1,i=1,2,⋯,n λ j = h j + 1 h j + h j + 1 , μ j = 1 − λ j \lambda_j = \dfrac{h_{j+1}}{h_j+h_{j+1}},\mu_j=1-\lambda_j λj=hj+hj+1hj+1,μj=1−λj d j = 6 f [ x j − 1 , x j , x j + 1 ] (二阶差商) j = 1 , 2 ⋯ , n − 1 d_j=6f\left[x_{j-1},x_j,x_{j+1}\right]\text{(二阶差商)}\quad j=1,2\cdots,n-1 dj=6f[xj−1,xj,xj+1](二阶差商)j=1,2⋯,n−1 d 0 = 6 h 1 ( f 1 − f 0 h 1 − f 0 ′ ) d n = 6 h n ( f n ′ − f n − f n − 1 h n ) d_0=\dfrac6{h_1}\left(\dfrac{f_1-f_0}{h_1}-f_0^{\prime}\right) \\ \ \\d_n=\dfrac6{h_n}\left(f_n^{\prime}-\dfrac{f_n-f_{n-1}}{h_n}\right) d0=h16(h1f1−f0−f0′) dn=hn6(fn′−hnfn−fn−1)
-
步骤 2 2 2: 代入线性方程组(3),并用追赶法解三对角方程组,得 M 0 , M 1 , ⋯ , M n M_0,M_1,\cdots,M_n M0,M1,⋯,Mn
-
步骤 3 3 3: (侧重点:如何把分段的效果表示出来)
得到 x x x点处的插值近似值 s ( x ) s(x) s(x)
Ⅱ型三次样条插值
输入
- n + 1 n+1 n+1 个插值节点 ( x i , y i ) , i = 0 , 1 , ⋯ , n (x_i,y_i),i=0,1,\cdots,n (xi,yi),i=0,1,⋯,n 构成向量 x 0 , y 0 x_0,y_0 x0,y0
- II 型边界条件 f 0 ′ ′ , f n ′ ′ f''_0,f''_n f0′′,fn′′
追赶法解三对角方程组(6)
Ⅲ型三次样条插值
前提:判断满足III型条件
输入
- n + 1 n+1 n+1 个插值节点 ( x i , y i ) , i = 0 , 1 , ⋯ , n (x_i,y_i),i=0,1,\cdots,n (xi,yi),i=0,1,⋯,n 构成向量 x 0 , y 0 x_0,y_0 x0,y0
另外
λ
n
=
h
1
/
(
h
1
+
h
n
)
,
μ
n
=
h
n
/
(
h
1
+
h
n
)
\lambda_n=h_1/(h_1+h_{n}),\mu_n=h_{n}/(h_1+h_{n})
λn=h1/(h1+hn),μn=hn/(h1+hn)
d
n
=
6
(
f
[
x
0
,
x
1
]
−
f
[
x
n
−
1
,
x
n
]
)
/
(
h
1
+
h
n
)
d_n=6(f[x_0,x_1]-f[x_{n-1},x_n])/(h_1+h_{n})
dn=6(f[x0,x1]−f[xn−1,xn])/(h1+hn)
解线性方程组(9)
三、北太天元 or matlab实现
Ⅰ型
function [s,M] = spline1_interp(x0,y0,df0,dfn,x)
% I型三次样条插值
% Input: 节点向量x0,y0,两个端点的一阶导 df0,df1
% 目标点 x
% Output: 插值结果 s , M
% 子函数:divided_differences,tridiag_chase
% Version: 1.0
% last modified: 04/14/2024
n = length(x0);
h = zeros(1,n-1); h = x0(2:n)-x0(1:n-1);
nh = length(h);
lamda = zeros(1,nh-1);
lamda = h(2:nh)./(h(1:nh-1)+h(2:nh));
mu = 1-lamda;
d= zeros(1,n);
% 计算差商
D = divided_differences(x0,y0,4)
d(2:n-1) = D(3:n,4); %取二阶差商
d(1) = 6/h(1) * ((y0(2)-y0(1))/h(1) - df0);
d(n) = 6/h(n-1) * (dfn - (y0(n)-y0(n-1))/h(n-1));
% 表示三对角方程组
A = diag(2*ones(1,n),0) + diag([mu,1],-1) +diag([1,lamda],1);
% 解三对角方程组
[M]=tridiag_chase(A,d);
% 分段表示
nx = length(x);
s = zeros(1,nx);
% 对于每个 x
for j = 1:1:nx
% 判断在哪个小区间
for i = 1:n-1
if x(j) >= x0(i) && x(j) <= x0(i+1)
hi = h(i); t2 = x0(i+1);t1 = x0(i);
M2 = M(i+1);M1 = M(i);
s(j) =1/(6*hi) * ((t2-x(j))^3 *M1 +(x(j) -t1)^3*M2);
s(j) = s(j) + 1/hi *( (t2-x(j)) * y0(i) + (x(j)- t1)*y0(i+1) );
s(j) = s(j) - hi/6 * ( (t2-x(j))*M1 + (x(j)-t1)*M2 );
break;
end
end
end
end
保存为spline1_interp.m文件
Ⅱ型
function [s,M] = spline2_interp(x0,y0,dff0,dffn,x)
% II型三次样条插值
% Input: 节点向量x0,y0,两个端点的二阶导 dff0,dff1
% 目标点 x
% Output: 插值结果 s , M
% 子函数:divided_differences,tridiag_chase
% Version: 1.0
% last modified: 04/14/2024
n = length(x0);
h = zeros(1,n-1); h = x0(2:n)-x0(1:n-1);
nh = length(h);
lamda = zeros(1,nh-1);
lamda = h(2:nh)./(h(1:nh-1)+h(2:nh));
mu = 1-lamda;
d= zeros(1,n-2);
% 计算差商
D = divided_differences(x0,y0,4);
d = D(3:n,4); %取二阶差商
d(1) = d(1) - mu(1)*dff0;
d(n-2) = d(n-2) - lamda(n-2)*dffn;
% 表示三对角方程组
A = diag(2*ones(1,length(d)),0) + diag(mu(2:nh-1),-1) +diag(lamda(1:nh-2),1);
% 解三对角方程组
[M]=tridiag_chase(A,d); % 得到的M 是列向量
M = [dff0;M;dffn];
% 分段表示
nx = length(x);
s = zeros(1,nx);
% 对于每个 x
for j = 1:1:nx
% 判断在哪个小区间
for i = 1:n-1
if x(j) >= x0(i) && x(j) <= x0(i+1)
hi = h(i); t2 = x0(i+1);t1 = x0(i);
M2 = M(i+1);M1 = M(i);
s(j) =1/(6*hi) * ((t2-x(j))^3 *M1 +(x(j) -t1)^3*M2);
s(j) = s(j) + 1/hi *( (t2-x(j)) * y0(i) + (x(j)- t1)*y0(i+1) );
s(j) = s(j) - hi/6 * ( (t2-x(j))*M1 + (x(j)-t1)*M2 );
break;
end
end
end
end
保存为 spline2_interp.m 文件
Ⅲ型
function [s,M] = spline3_interp(x0,y0,x)
% III 型三次样条插值
% Input: 节点向量x0,y0
% 目标点 x
% Output: 插值结果 x , M
% 子函数:divided_differences,myJocabi
% Version: 1.0
% last modified: 04/14/2024
n = length(x0);
h = zeros(1,n-1); h = x0(2:n)-x0(1:n-1);
nh = length(h);
lamda = zeros(1,nh-1);
lamda = h(2:nh)./(h(1:nh-1)+h(2:nh));
mu = 1-lamda;
d= zeros(1,n-1);
% 计算差商
D = divided_differences(x0,y0,4);
d(1:n-2) = D(3:n,4) %取二阶差商
% 从D中取差商时,注意位置和n的关系
d(n-1) = 6*(D(2,3)-D(n,3))/(h(1)+h(nh));
mu = [mu,h(nh)/(h(1)+h(nh))];
% 表示方程组
A = diag(2*ones(1,length(d)),0) + diag(mu(2:nh),-1) +diag(lamda,1);
A(1,n-1) = mu(1);
A(n-1,1) = h(1)/(h(1)+h(nh));
% 用Jacobi迭代法进行求解
[M]=myJacobi(A,d',zeros(1,length(d)),10e-8,100); % 得到的M 是列向量
M = M(:,end);
M=[M(1);M];
% 分段表示
nx = length(x);
s = zeros(1,nx);
% 对于每个 x
for j = 1:1:nx
% 判断在哪个小区间
for i = 1:n-1
if x(j) >= x0(i) && x(j) <= x0(i+1)
hi = h(i); t2 = x0(i+1);t1 = x0(i);
M2 = M(i+1);M1 = M(i);
s(j) =1/(6*hi) * ((t2-x(j))^3 *M1 +(x(j) -t1)^3*M2);
s(j) = s(j) + 1/hi *( (t2-x(j)) * y0(i) + (x(j)- t1)*y0(i+1) );
s(j) = s(j) - hi/6 * ( (t2-x(j))*M1 + (x(j)-t1)*M2 );
break;
end
end
end
end
保存为 spline3_interp.m 文件
四、数值算例
1. 课本上一个例子
求三次插值样条函数
s
(
x
)
s(x)
s(x),边界条件
s
′
(
x
0
)
=
f
0
′
=
1
,
s
′
(
x
3
)
=
f
3
′
=
0
s'(x_0)=f_0'=1,\quad s'(x_3)=f_3'=0
s′(x0)=f0′=1,s′(x3)=f3′=0
插值条件
| x i x_i xi | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| f i f_i fi | 0 | 0 | 0 | 0 |
满足Ⅰ型插值条件,使用Ⅰ次样条插值:
%% 1 I 型三次样条插值 课本P55 例2.13
clc;clear all;
x0 = [0 1 2 3];
y0 = [0 0 0 0];
df0 = 1;dfn = 0;
x = 1/2;
[s,M] = spline1_interp(x0,y0,df0,dfn,x)
x= linspace(0,3);
s = spline1_interp(x0,y0,df0,dfn,x);
plot(x,s)
hold on
plot (x0,y0,'o')
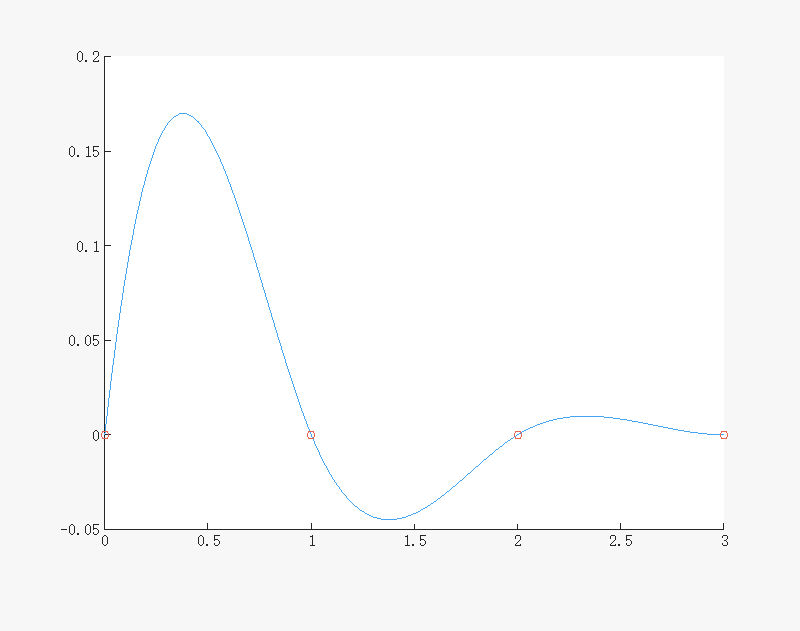
得到
M =
-3.4667
0.9333
-0.2667
0.1333
图像如下
2. Runge函数下的表现
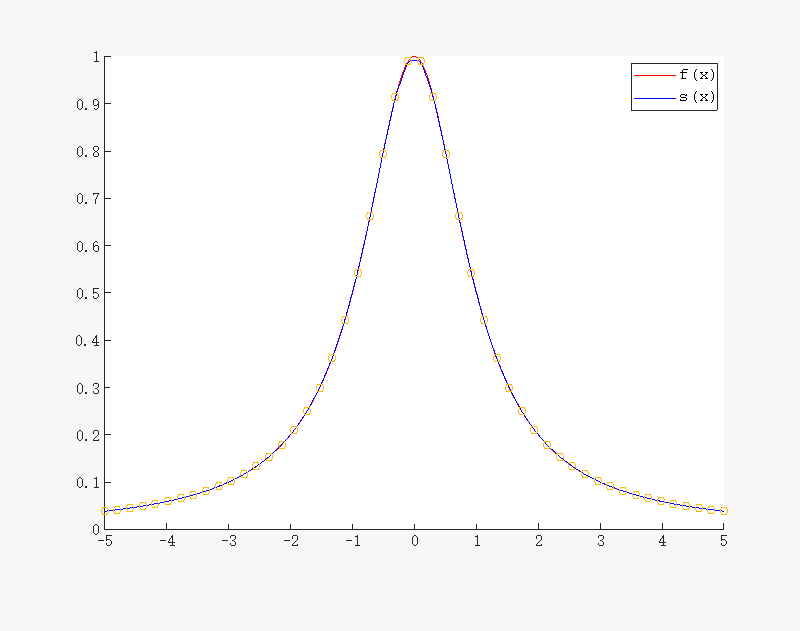
f ( x ) = 1 x 2 + 1 , x ∈ [ − 5 , 5 ] f(x) = \dfrac{1}{x^2+1},x\in[-5,5] f(x)=x2+11,x∈[−5,5]
%% 4 Runge函数下的表现
clc;clear all;format long;
Runge = @(x)1./(x.^2+1);
x0 = linspace(-5,5,50);
y0 = Runge(x0);
df0 = 10/(25+1)^2; dfn = -10/(25+1)^2;
x=linspace(-5,5,200);
y = Runge(x);
s = spline1_interp(x0,y0,df0,dfn,x);
plot(x,y,'r');
hold on
plot(x,s,'b');
plot(x0,y0,'o');
legend('f(x)','s(x)')
hold off
令 delta = max(abs(y- s));
delta随 n 的变化
| n | delta |
|---|---|
| 10 | 0.219763153253344 |
| 20 | 0.055477054367970 |
| 30 | 0.023824006347768 |
| 40 | 0.013017783894429 |
| 50 | 0.008083997855805 |
| 100 | 0.001595156336341 |
可以看到,随着n的增大,误差越来越小, s ( x ) s(x) s(x) 越趋近于 f ( x ) f(x) f(x)
3. Ⅱ型
%% 2 II 型三次样条插值 y = x^3
clc;clear all;
x0 = linspace(0,3,10);
y0 = x0.^3;
dff0 = 0;dffn = 18;
x= linspace(0,3,200);
y = x.^3;
[s,M] = spline2_interp(x0,y0,dff0,dffn,x);
plot(x,y,'r');
hold on
plot(x,s,'b');
hold off
所编写的Ⅱ型三次样条插值代码也是可以正常运行的.
4. Ⅲ型
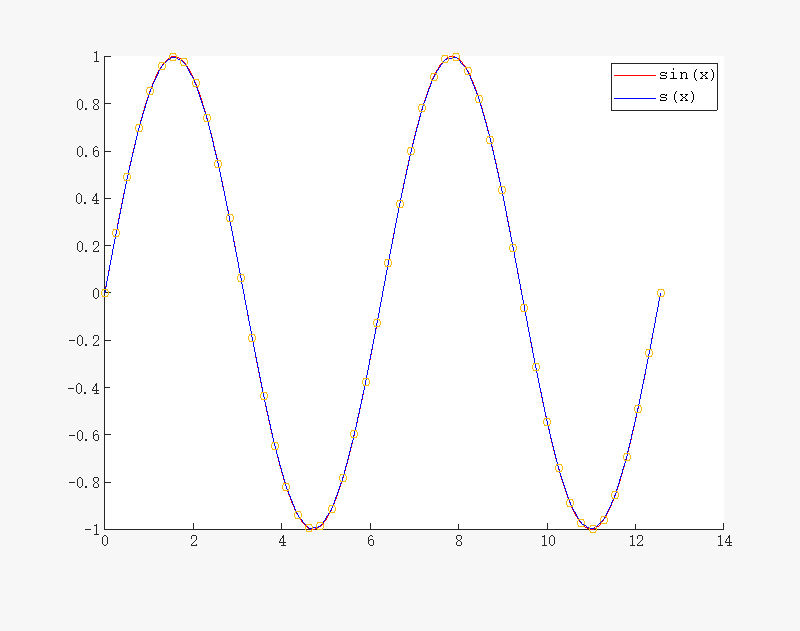
%% 3 III 型三次样条插值 y =sin(x)
clc;clear all;
x0 = linspace(0,4*pi,50);
y0 = sin(x0);
x= linspace(0,4*pi,200);
y = sin(x);
[s,M] = spline3_interp(x0,y0,x);
plot(x,y,'r');
hold on
plot(x,s,'b');
plot(x0,y0,'o');
legend('sin(x)','s(x)')
hold off
Ⅲ型一般用于循环的情况. 可以看到,我们的代码实现效果是正常的.
三次样条插值的主要优点:
- 平滑性: 二阶连续可微
- 全局性: 考虑了所有的数据点,能够反映整体数据的趋势和特征
在实现过程中用到