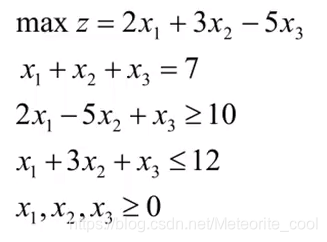matlab中线性规划问题主要借助于linprog函数,这个函数通过矩阵:Ax=b的原理求解结果。
1. 普通线性规划问题
例1.某机床厂生产甲、乙两种机床,每台销售后的利润分别为4千元与3千元。生产甲机床需用A、B机器加工, 加工时间分别为每台2小时和1小时;生产乙机床需用A、B、C三种机器加工,加工时间为每台各一小时。若每天可用于加工的机器时数分别为A机器10小时、B机器8小时和C机器7小时,问该厂应生产甲、乙机床各几台,才能使总利润最大?
符号说明
| 符号 | 含义 |
|---|---|
| a | 生产甲的数量 |
| b | 生产乙的数量 |
| z | 目标值 |
(1)列出约束条件与目标函数
目标函数:·求max: z=4a+3b
约束条件:
- 2a+b<10;
- a+b<8;
- b<7;
(2) 调用matlab函数
(1)函数介绍:
需要调用linprog函数,格式如下:
[x,fval]=linprog(f,a,b,aeq,beq,lb,up,options)
其中,
- x为取得最值时自变量x的取值;
- fval为取得最值时最值的值; f为目标函数,本题中为:z=4a+3b,表示为[4,3](线代知识)
- a,b为不等约束,其中a为不等约束左边系数,b为不等约束右边系数。
- aeq,beq为等式约束,aeq为等式左边系数,beq为等式右边系数.
- lb,up分别为自变量自身取值范围。本题中a,b取值范围均为[0,+∞].
- options为使用的方法种类,一般不做更改。
- 注意,linprog函数默认求目标函数最小值,所以如果要求最大值需要使目标函数系数乘以-1;
- linprog函数不等约束方程里默认为Ax<b的形式,如果你得出Bx>C的约束方程,需要乘以-1变成(-B)x<-C的形式。
(2)调用函数:
[x,fval]=linprog([-4,-3],[2,1;1,1;0,1],[10;8;7],[0,0;0,0;0,0],[0;0;0],[0,0],[inf,inf]);
fval=-fval
(3)输出结果:
Optimal solution found.
x =
2.0000
6.0000
fval =
26
(4)代码解释:
1.matlab中linprog函数默认求解目标函数最小值,而题目中为了求解最大值,所以把目标函数系数[4,3]改为[-4,-3],再由fval=-fval求出最大值。
2.由于本题没有等式约束,自变量的取值范围也没有额外要求,所以aeq,beq部分为零矩阵,lb也为零矩阵,ub为无限大。(matlab中inf为+∞),所以上述主要代码也可以缩减为:
[x,fval]=linprog([-4,-3],[2,1;1,1;0,1],[10;8;7])
(3)练习:
代码如下:
[x,fval]=linprog([-2,-3,5],[-2,5,-1;1,3,1],[-10,12],[1,1,1],[7],[0,0,0],[inf,inf,inf])
fval=-fval