百题分类

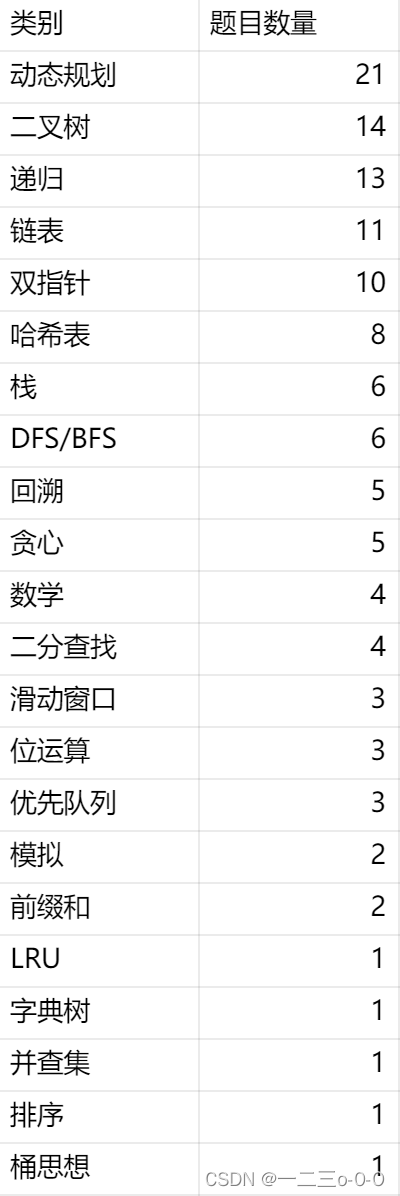
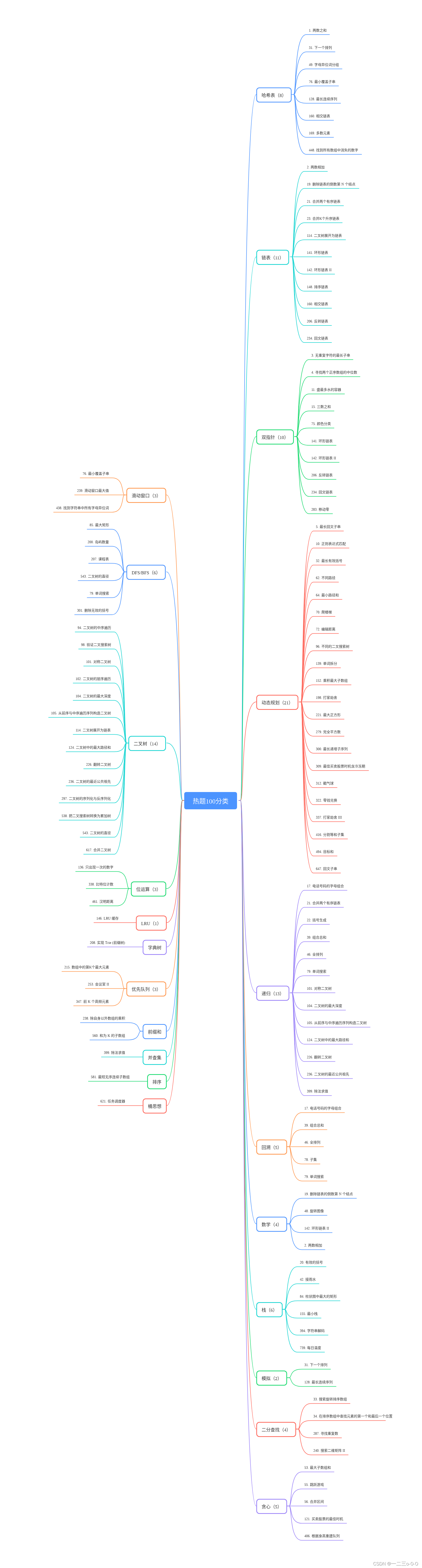
将一百题共分为22个类别

具体频率统计

脑图统计

百题题解

1. 1. 两数之和

// 哈希表
class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int,int> unMap;
        
        for(int i{};i<nums.size();++i){
            if(unMap.find(target - nums[i]) != unMap.end()){
                return {i,unMap[target - nums[i]]};
            }

            unMap[nums[i]] = i;
        }

        return {};
    }
};

2. 2. 两数相加

// 链表+数学相加进位

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        ListNode *head{};
        ListNode *tail{};


        int carry{};
        while(l1 || l2){
            int num1 = l1 ? l1->val : 0;
            int num2 = l2 ? l2->val : 0;

            int sum = num1 + num2 + carry;

            if(!head){
                head = tail = new ListNode(sum%10);
            }else{
                tail->next = new ListNode(sum%10);;
                tail = tail->next;
            }

            carry = sum/10;

            if(l1) l1 = l1->next;
            if(l2) l2 = l2->next;
        }

        if(carry > 0) tail->next= new ListNode(carry);


        return head;
    }
};

3. 3. 无重复字符的最长子串

// 双指针
class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char,int>need;

        int n = s.size();
        if(0 == n) return 0;

        int left{},right{1},result{1};
        need[s[left]]++;
        for(;right < n;++right){
            if(need[s[right]] > 0){
                while(need[s[right]] > 0){
                    need[s[left++]]--;
                }
            }
            need[s[right]]++;
            result = max(result,right-left+1);
        }

        return result;
    }
};

4. 4. 寻找两个正序数组的中位数

// 二分查找
class Solution {
public:
    int getKthElement(const vector<int>& nums1, const vector<int>& nums2, int k) {
        /* 主要思路：要找到第 k (k>1) 小的元素，那么就取 pivot1 = nums1[k/2-1] 和 pivot2 = nums2[k/2-1] 进行比较
         * 这里的 "/" 表示整除
         * nums1 中小于等于 pivot1 的元素有 nums1[0 .. k/2-2] 共计 k/2-1 个
         * nums2 中小于等于 pivot2 的元素有 nums2[0 .. k/2-2] 共计 k/2-1 个
         * 取 pivot = min(pivot1, pivot2)，两个数组中小于等于 pivot 的元素共计不会超过 (k/2-1) + (k/2-1) <= k-2 个
         * 这样 pivot 本身最大也只能是第 k-1 小的元素
         * 如果 pivot = pivot1，那么 nums1[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums1 数组
         * 如果 pivot = pivot2，那么 nums2[0 .. k/2-1] 都不可能是第 k 小的元素。把这些元素全部 "删除"，剩下的作为新的 nums2 数组
         * 由于我们 "删除" 了一些元素（这些元素都比第 k 小的元素要小），因此需要修改 k 的值，减去删除的数的个数
         */

        int m = nums1.size();
        int n = nums2.size();
        int index1 = 0, index2 = 0;

        while (true) {
            // 边界情况
            if (index1 == m) {
                return nums2[index2 + k - 1];
            }
            if (index2 == n) {
                return nums1[index1 + k - 1];
            }
            if (k == 1) {
                return min(nums1[index1], nums2[index2]);
            }

            // 正常情况
            int newIndex1 = min(index1 + k / 2 - 1, m - 1);
            int newIndex2 = min(index2 + k / 2 - 1, n - 1);
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];
            if (pivot1 <= pivot2) {
                k -= newIndex1 - index1 + 1;
                index1 = newIndex1 + 1;
            }
            else {
                k -= newIndex2 - index2 + 1;
                index2 = newIndex2 + 1;
            }
        }
    }

    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int totalLength = nums1.size() + nums2.size();
        if (totalLength % 2 == 1) {
            return getKthElement(nums1, nums2, (totalLength + 1) / 2);
        }
        else {
            return (getKthElement(nums1, nums2, totalLength / 2) + getKthElement(nums1, nums2, totalLength / 2 + 1)) / 2.0;
        }
    }
};

5. 5. 最长回文子串

// 动态规划

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        // dp,拆解子问题：dp(i+1,j+1)为回文子串 并且size 》 2 ，那么dp[i,j]也是回文子串
        vector<vector<int>> dp(n,vector<int>(n));

        for(int i{};i<n;++i){
            dp[i][i] = 1;
        }

        int result{},begin{};
        for(int length{2};length <= n;++length){
            for(int i{};i<n-length+1;++i){
                if(2 == length){
                    if(s[i] == s[i+length-1]){
                        dp[i][i+length-1] = 1;
                        begin = i;
                        result = 2;
                    }
                }else{
                    if(s[i] == s[i+length-1] && dp[i+1][i+length-2] == 1){
                        dp[i][i+length-1] = 1;
                        begin = i;
                        result = length;
                    }
                }
            }
        }

        return result > 1 ? s.substr(begin,result) : s.substr(0,1);
    }
};

6. 10. 正则表达式匹配
   状态转移方程的优化：
   

// 动态规划

class Solution {
public:
    bool isMatch(string s, string p) {
        int m = s.size();
        int n = p.size();
        // 1.状态定义：dp[i][j]表示前i个字符与p中前j个字符是否能够匹配
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        dp[0][0] = true;
        auto match = [&](int i,int j){
            if(i == 0) return false;
            if(p[j-1] == '.') return true;

            if(s[i-1] == p[j-1]) return true;

            return false;
        };

        for(int i{};i<=m;++i){
            for(int j{1};j<=n;++j){
                if(p[j-1] == '*'){
                    dp[i][j] |= dp[i][j-2];

                    if(match(i,j-1)){
                        dp[i][j] |= dp[i-1][j];
                    }
                }else{
                    if(match(i,j)){
                        dp[i][j] |= dp[i-1][j-1];
                    }
                }
            }
        }

        return dp[m][n];
    }
};

7. 11. 盛最多水的容器

// 双指针
class Solution {
public:
    int maxArea(vector<int>& height) {
        int n = height.size();
        int left{};
        int right = n-1;

        int result{};
        while(left < right){
            int h = min(height[left],height[right]);
            int width = right - left;

            result = max(result,h*width);

            if(h < height[left]){
                right--;
            }else{
                left++;
            }
        }

        return result;
    }
};

8. 15. 三数之和

// 双指针
class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> result;

        int n = nums.size();

        sort(nums.begin(),nums.end());

        for(int i{};i<n-2;++i){
            if(i && nums[i] == nums[i-1])continue;
            int left = i+1;
            int right = n-1;

            while(left < right){
                if(nums[i] + nums[left] + nums[right] == 0){
                    result.push_back({nums[i],nums[left],nums[right]});

                    while(left < right && nums[left] == nums[left+1]){
                        ++left;
                    }

                    while(left < right && nums[right] == nums[right-1]){
                        --right;
                    }

                    --right;
                    ++left;
                }else if(nums[i] + nums[left] + nums[right] < 0){
                    ++left;
                }else{
                    --right;
                }
            }
        }
        return result;
    }
};

9. 17. 电话号码的字母组合

// 递归+回溯
class Solution {
public:
    vector<string> v{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    vector<string> result;
    string path;

    void recursive(string digits,int index){
        if(path.size() == digits.size()){
            result.push_back(path);
            return;
        }

        string s = v[digits[index] - '0'];

        for(int i {};i<s.size();++i){
            path.push_back(s[i]);

            recursive(digits,index+1);

            path.pop_back();
        }
    }

    vector<string> letterCombinations(string digits) {
        if(digits.size() == 0) return {};
        recursive(digits,0);

        return result;
    }
};

11. 19. 删除链表的倒数第 N 个结点

// 链表+数学计算
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* removeNthFromEnd(ListNode* head, int n) {
        int count{};

        // 删除倒数第n个，即删除第count-n+1

        ListNode* cNode = head;

        while(cNode != nullptr){
            cNode = cNode->next;
            count++;
        }

        ListNode *cNodeX = new ListNode(0);
        cNodeX->next = head;
        count = count - n +1;

        ListNode *node = cNodeX;
        while(count--){
            if(0 == count){
                node->next = node->next->next;
                break;
            }
            node = node->next;
        }

        return cNodeX->next;
    }
};

12. 20. 有效的括号

// 栈
class Solution {
public:
    bool isValid(string s) {
        stack<char> st;

        int n = s.size();

        for(int i{};i<n;++i){
            if(s[i] == '('){
                st.push(')');
            }else if(s[i] == '['){
                st.push(']');
            }else if(s[i] == '{'){
                st.push('}');
            }else{
                if(st.empty() || st.top() != s[i]) return false;

                st.pop();
            }
        }

        return st.empty();
    }
};

13. 21. 合并两个有序链表

// 链表+递归
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        if(!list1) return list2;
        if(!list2) return list1;

        ListNode* node{nullptr};

        if(list1->val < list2->val){
            node = list1;
            list1 = list1->next;
        }else{
            node = list2;
            list2 = list2->next;
        }

        node->next = mergeTwoLists(list1,list2);

        return node;
    }
};

14. 22. 括号生成

// 递归
class Solution {
public:
    vector<string> result;
    void solve(int open,int close,string str){
        if(0 == open && 0 == close){
            result.push_back(str);
            return;
        }

        if(open > 0){
            string s = str;
            s.push_back('(');
            solve(open-1,close,s);
        }

        if(close > open){
            string s = str;
            s.push_back(')');
            solve(open,close-1,s);
        }
    }
    vector<string> generateParenthesis(int n) {
        int open = n;
        int close = n;

        solve(open,close,"");

        return result;
    }
};

15. 23. 合并K个升序链表

// 链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1,ListNode* list2){
        if(!list1) return list2;
        if(!list2) return list1;

        ListNode* node = new ListNode(0);
        ListNode* tail = node;
        
        while(list1 && list2){
            if(list1->val < list2->val){
                tail->next = list1;
                list1 = list1->next;
            }else{
                tail->next = list2;
                list2 = list2->next;
            }

            tail = tail->next;
        }

        tail->next = list1 ? list1 : list2;

        return node->next;;
    }
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        int k = lists.size();


        ListNode* node{};

        for(int i{};i<k;++i){
            node = mergeTwoLists(node, lists[i]);
        }

        return node;
    }
};

16. 31. 下一个排列

// 哈希表+模拟
class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        //[4,5,2,6,3,1]
        // 先找较小数
        int n = nums.size();

        int minIndex = n-2;

        for(;minIndex >=0;--minIndex){
            if(nums[minIndex] < nums[minIndex+1]){
                break;
            }
        }
        // 再找较大数
        int maxIndex{};
        if(minIndex >= 0){ // 这步边界条件判断很重要
            for(int i{n-1};i>=0;--i){
                if(nums[i] > nums[minIndex]){
                    maxIndex = i;
                    break;
                }
            }

            // 交换两个数，并将较大数的右侧降序序列翻转为升序序列
            swap(nums[minIndex],nums[maxIndex]);
        }
        reverse(nums.begin() + minIndex+1,nums.end());
    }
};

17. 32. 最长有效括号

// 动态规划
class Solution {
public:
    int longestValidParentheses(string s) {
        int n = s.size();
        // 1.dp数组定义：dp[i] 表示s[i]字符结尾的的最长有效括号字串的长度
        vector<int> dp(n,0);
        int result{};
        // 3.确定便利顺序，从下标1开始遍历即可
        for(int i{1};i<n;++i){
            if('(' == s[i]){
                continue;
            }
            // 2.确定递推公式
            if(s[i-1] == '('){
                dp[i] = 2;
                if(i-2 >= 0){
                    dp[i]+=dp[i-2];
                }
            }else if(dp[i-1] > 0){
                if((i-dp[i-1]-1) >= 0 && s[i-dp[i-1]-1] == '('){
                    dp[i] = dp[i-1]+2;
                    if((i-dp[i-1]-2) >= 0){
                        dp[i] += dp[i-dp[i-1]-2];
                    }
                }
            }

            result = max(result,dp[i]);
        }

        return result;
    }
};

18. 33. 搜索旋转排序数组

// 二分查找
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left{},right = nums.size()-1;

        while(left <= right){
            int mid = (left + right)/2;

            if(nums[mid] == target){
                return mid;
            }else if(nums[mid] >= nums[left]){
                if(target <= nums[mid] && target >= nums[left]){
                    right = mid-1;
                }else{
                    left = mid +1;
                }
            }else{
                if(target >= nums[mid] && target <= nums[right]){
                    left = mid + 1;
                }else{
                    right = mid -1;
                }
            }
        }

        return -1;
    }
};

19. 34. 在排序数组中查找元素的第一个和最后一个位置

// 二分查找
class Solution {
public:
    vector<int> searchRange(vector<int>& nums, int target) {
        // 先找数组中第一个不小于target的元素
        auto left = lower_bound(nums.begin(),nums.end(),target);
        // 找数组中大于目标值的第一个元素
        auto right = upper_bound(nums.begin(),nums.end(),target);
        if(left == right) return {-1,-1};

        return {(int)(left-nums.begin()),(int)(right-nums.begin() -1)};
    }
};

20. 39. 组合总和

// 递归+回溯
class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;
    void backTracking(vector<int>& candidates,int target,int sum,int index){
        if(sum > target){
            return;
        }
        if(target == sum){
            result.push_back(path);
            return;
        }

        for(int i{index};i<candidates.size();++i){
            sum+=candidates[i];
            path.push_back(candidates[i]);
            // 递归传进去的是i,不是index，也不是index+1，因为不需要进行递归层数的限制
            backTracking(candidates,target,sum,i);
            sum-=candidates[i];
            path.pop_back();
        }
    }
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backTracking(candidates,target,{},0);
        return result;
    }
};

21. 42. 接雨水

// 单调栈
class Solution {
public:
    int trap(vector<int>& height) {
        int ans = 0;
        stack<int> stk;
        int n = height.size();
        for (int i = 0; i < n; ++i) {
            while (!stk.empty() && height[i] > height[stk.top()]) {
                int top = stk.top();
                stk.pop();
                if (stk.empty()) {
                    break;
                }
                int left = stk.top();
                int currWidth = i - left - 1;
                int currHeight = min(height[left], height[i]) - height[top];
                ans += currWidth * currHeight;
            }
            stk.push(i);
        }
        return ans;
    }
};

22. 46. 全排列

// 递归+回溯
class Solution {
public:
    // 核心是要利用used数组
    vector<vector<int>> result;
    vector<int> path;
    void backTracking(vector<int>& nums,vector<bool>& used){
        if(nums.size() == path.size()){
            result.push_back(path);
            return;
        }

        for(int i{};i<nums.size();++i){
            if(used[i] == true) continue;

            used[i] = true;
            path.push_back(nums[i]);
            backTracking(nums,used);
            path.pop_back();
            used[i] = false;
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<bool> used(nums.size());
        backTracking(nums,used);
        return result;
    }
};

23. 48. 旋转图像

// 数学逻辑
class Solution {
public: 
    // 重点是找到规律：对于矩阵中第 i 行的第 j 个元素，在旋转后，它出现在倒数第 i 列的第 j 个位置。
    // 即matrix[r][c] 在旋转后，新的位置是matrix[c][n-r-1]

    // 借助辅助数组
    // void rotate(vector<vector<int>>& matrix) {
    //     auto mNew = matrix;
    //     int n = matrix.size();
    //     for(int i{};i<n;++i){
    //         for(int j{};j<n;++j){
    //             mNew[j][n-i-1] = matrix[i][j];
    //         }
    //     }

    //     matrix = mNew;
    // }
    // 利用翻转代替旋转
    // 水平翻转：matrix[r][c] = matrix[n-row-1][c]
    // 主对角线翻转: matrix[r][c] = matrix[c][r]
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        
        for(int i{};i<n/2;++i){
            for(int j{};j<n;++j){
                swap(matrix[i][j] , matrix[n-i-1][j]);
            }
        }

        for(int i{};i<n;++i){
            for(int j{};j<i;++j){
                swap(matrix[i][j] , matrix[j][i]);
            }
        }
    }
};

24. 49. 字母异位词分组

// 哈希表
class Solution {
public:
    vector<vector<string>> groupAnagrams(vector<string>& strs) {
        unordered_map<string,vector<string>> unMap;

        for(int i{};i<strs.size();++i){
            string s = strs[i];
            sort(s.begin(),s.end());

            unMap[s].push_back(strs[i]);
        }
        vector<vector<string>> result;
        for(auto [key,value] : unMap){
            result.push_back(value);
        }

        return result;
    }
};

25. 53. 最大子数组和

// 贪心
class Solution {
public:
    // 贪心
    int maxSubArray(vector<int>& nums) {
        int result{INT_MIN};
        int sum{};
        for(int i{};i<nums.size();++i){
            sum+=nums[i];
            if(sum > result) result = sum;
            if(sum < 0) sum = 0;
        }

        return result;
    }
};

26. 55. 跳跃游戏

// 贪心
class Solution {
public:
    bool canJump(vector<int>& nums) {
        int n = nums.size();

        int maxJump{};
        for(int i{};i<n;++i){
            maxJump = max(maxJump,i+nums[i]);

            if(maxJump >= n-1) return true;
            if(maxJump < i+1){
                return false;
            }
        }

        return true;
    }
};

27. 56. 合并区间

// 贪心
class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        vector<vector<int>> result;
        int n = intervals.size();

        sort(intervals.begin(),intervals.end());

        bool falg{false};
        for(int i{1};i<n;++i){
            int start = intervals[i-1][0];
            int end   = intervals[i-1][1];

            while(i<n && intervals[i][0] <= end){
                end = max(intervals[i][1],end);
                if(i == n-1) falg = true;
                ++i;
            }
            result.push_back({start,end});
        }

        if(!falg) result.push_back(intervals.back());

        return result;
    }
};

28. 62. 不同路径

// 动态规划
class Solution {
public:
    int uniquePaths(int m, int n) {
        vector<vector<int>> dp(m,vector<int>(n));

        for(int i{};i<m;++i) dp[i][0] = 1;
        for(int j{};j<n;++j) dp[0][j] = 1;
        

        for(int i{1};i<m;++i){
            for(int j{1};j<n;++j){
                dp[i][j] = dp[i-1][j] + dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
};

28. 64. 最小路径和

// 动态规划
class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();

        vector<vector<int>> dp(m,vector<int>(n));

        dp[0][0] = grid[0][0];
        for(int i{1};i<m;++i) dp[i][0] = grid[i][0] + dp[i-1][0];
        for(int i{1};i<n;++i) dp[0][i] = grid[0][i] + dp[0][i-1];

        for(int i{1};i<m;++i){
            for(int j{1};j<n;++j){
                dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j];
            }
        }

        return dp[m-1][n-1];
    }
};

29. 70. 爬楼梯

// 动态规划
class Solution {
public:
    int climbStairs(int n) {
        // fn = fn-1+fn-2
        if(n <= 3) return n;

        vector<int> dp(n+1);
        dp[2] = 2;
        dp[3] = 3; 
        for(int i{4};i<=n;++i){
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }
};

30. 72. 编辑距离

// 动态规划
class Solution {
public:
	// 583.两个字符串的删除操作的变形
    using LL = unsigned long long;
    int minDistance(string word1, string word2) {
        int len1 = word1.size();
        int len2 = word2.size();
		// 1.定义dp数组以及数组下标的含义
		// dp[i][j]:字符串word1[0,i] 与word2[0,j]，将 word1 转换成 word2 所使用的最少操作数为dp[i][j]
        vector<vector<LL>> dp(len1+1,vector<LL>(len2+1));
        // 3.dp数组初始化
        for(int i{};i<=len1;++i) dp[i][0] = i;
        for(int j{};j<=len2;++j) dp[0][j] = j;
        // 4.确定遍历顺序
        for(int i{1};i<=len1;++i){
            for(int j{1};j<=len2;++j){
            	// 2.确定递推公式
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    dp[i][j] = min({dp[i-1][j-1],dp[i][j-1],dp[i-1][j]}) + 1;
                }
            }
        }

        return dp[len1][len2];
    }

31. 75. 颜色分类

// 双指针求解:经典的荷兰国旗问题
class Solution {
public:
    void sortColors(vector<int>& nums) {
        int p0{},p1{};

        int n = nums.size();

        for(int i{};i<n;++i){
            if(nums[i] == 1){
                swap(nums[i],nums[p1++]);
            }else if(nums[i] == 0){
                swap(nums[i],nums[p0]);
                if(p0 < p1){
                    swap(nums[i],nums[p1]);
                }
                ++p0;
                ++p1;
            }
        }
    }
};

32. 76. 最小覆盖子串

// 滑动窗口+哈希表
class Solution {
public:
    string minWindow(string s, string t) {
        vector<int> need(128);

        for(char c : t) need[c]++;

        int left{},right{};
        int start{};
        int count = t.size();
        int size = INT_MAX;

        for(;right < s.size();++right){
            char c = s[right];
            if(need[c] > 0) count--;// 进行一次匹配
            need[c]--;// 将右边的字符+入窗口内

            if(count == 0){ // 当都匹配到以后才需要进行窗口的缩减
                // 缩减窗口（因为题目要求是最小子串，所以需要让need[s[left]] == 0）
                while(left < right && need[s[left]] < 0){
                    need[s[left++]]++;
                }

                if(right - left + 1 < size){    
                    size = right - left + 1;
                    start = left;
                }

                need[s[left++]]++;// 左边界右移
                count++;// 哈希表又存储了一次，所以count要++
            }
        }

        return size == INT_MAX ? "" : s.substr(start,size);
    }
};

33. 78. 子集

// 回溯
class Solution {
public:
    vector<vector<int>> result;
    vector<int> path;

    void recursive(vector<int>& nums,int index){
        if(index > nums.size()){
            return;
        }

        result.push_back(path);

        for(int i = index;i<nums.size();++i){
            path.push_back(nums[i]);
            recursive(nums, i+1);
            path.pop_back();
        }
    }
    vector<vector<int>> subsets(vector<int>& nums) {
        recursive(nums,0);
        return result;
    }
};

34. 79. 单词搜索

// 递归+回溯（网格类型）
class Solution {
public:
    //定义方向
    int dx[4]{1,0,-1,0};
    int dy[4]{0,-1,0,1};
    
    //递归+回溯
    bool dfs(vector<vector<char>>& board,string word,int k,int i,int j,vector<vector<int>> &visit){
    	// 递归终止条件
        if(word[k] != board[i][j]){
            return false;
        }else if(k == word.size() -1){
            return true;
        }

        visit[i][j] = 1; // 表示已经被访问过
        bool result = false;
        // 横向遍历四个方向
        for(int d{};d<4;++d){
        	// 设置方向
            int i1 = i + dx[d];
            int j1 = j + dy[d];

            if(min(i1,j1) < 0 || i1 >=board.size() || j1 >= board[0].size()){
                continue;
            }

            if(1 == visit[i1][j1]) continue;
            // 根据方向纵向遍历
            if(dfs(board,word,k+1,i1,j1,visit)){
                result = true;
                break;
            } 
        }
        
        visit[i][j] = 0; // 回溯
        return result;
    }
    bool exist(vector<vector<char>>& board, string word) {
        int m = board.size(),n = board[0].size();
        vector<vector<int>> visit(m,vector<int>(n));
        // 先暴力，以每个字符为起点进行递归
        for(int i{};i<m;++i){
            for(int j{};j<n;++j){
                bool flag{false};
                flag = dfs(board,word,0,i,j,visit);
                if(flag) return true;
            }
        }
        return false;
    }
};

35. 84. 柱状图中最大的矩形

// 单调栈
class Solution {
public:
    int largestRectangleArea(vector<int>& heights)
	{
	    int ans = 0;
	    vector<int> st;
	    // 增加一个哨兵、与链表的哨兵节点一致
	    heights.insert(heights.begin(), 0);
	    // 尾部也要增加一个哨兵节点
	    heights.push_back(0);
	    for (int i = 0; i < heights.size(); i++)
	    {
	    	// 单调递增栈非空 and 或者遇到比栈顶元素小的元素
	        while (!st.empty() && heights[st.back()] > heights[i])
	        {
	            int cur = st.back(); // 要计算的柱体下标
	            st.pop_back();
	            int left = st.back() + 1;// 弹出当前下标后，现有栈的最大值的下标+1
	            int right = i - 1;// 当前柱体下标-1
	            // 宽=组成柱体的两边的下标相减+1
	            ans = max(ans, (right - left + 1) * heights[cur]);
	        }
	        st.push_back(i);
	    }
	    return ans;
	}
};

36. 85. 最大矩形

// 广度优先遍历（DFS）
class Solution {
public:
    int maximalRectangle(vector<vector<char>>& matrix) {
        int m = matrix.size();
        if (m == 0) {
            return 0;
        }
        int n = matrix[0].size();
        // 使用二维数组left 记录，其中left[i][j] 为矩阵第 i 行第 j 列元素的左边连续 1 的数量
        vector<vector<int>> left(m, vector<int>(n, 0));

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    left[i][j] = (j == 0 ? 0: left[i][j - 1]) + 1;
                }
            }
        }

        int ret = 0;
        // 一直计算的都是以matrix[i][j] 为右下角的矩形
        for (int j = 0; j < n; j++) { // 对于每一列，使用基于柱状图的方法
            vector<int> up(m, 0), down(m, 0);

            stack<int> stk;
            for (int i = 0; i < m; i++) {
                while (!stk.empty() && left[stk.top()][j] >= left[i][j]) {
                    stk.pop();
                }
                up[i] = stk.empty() ? -1 : stk.top();
                stk.push(i);
            }
            stk = stack<int>();
            for (int i = m - 1; i >= 0; i--) {
                while (!stk.empty() && left[stk.top()][j] >= left[i][j]) {
                    stk.pop();
                }
                down[i] = stk.empty() ? m : stk.top();
                stk.push(i);
            }

            for (int i = 0; i < m; i++) {
                int height = down[i] - up[i] - 1;
                int area = height * left[i][j];
                ret = max(ret, area);
            }
        }
        return ret;
    }
};
// 写法2：直接复用84
class Solution {
public:

    int largestRectangleArea(vector<int>& heights)
	{
	    int ans = 0;
	    vector<int> st;
	    // 增加一个哨兵、与链表的哨兵节点一致
	    heights.insert(heights.begin(), 0);
	    // 尾部也要增加一个哨兵节点
	    heights.push_back(0);
	    for (int i = 0; i < heights.size(); i++)
	    {
	    	// 单调递增栈非空 and 或者遇到比栈顶元素小的元素
	        while (!st.empty() && heights[st.back()] > heights[i])
	        {
	            int cur = st.back(); // 要计算的柱体下标
	            st.pop_back();
	            int left = st.back() + 1;// 弹出当前下标后，现有栈的最大值的下标+1
	            int right = i - 1;// 当前柱体下标-1
	            // 宽=组成柱体的两边的下标相减+1
	            ans = max(ans, (right - left + 1) * heights[cur]);
	        }
	        st.push_back(i);
	    }
	    return ans;
	}

    int maximalRectangle(vector<vector<char>>& matrix) {
        int m = matrix.size();
        if (m == 0) {
            return 0;
        }
        int n = matrix[0].size();
        vector<vector<int>> left(m, vector<int>(n, 0));

        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {
                    left[i][j] = (j == 0 ? 0: left[i][j - 1]) + 1;
                }
            }
        }
        int ret{};
        for(int j{};j<n;++j){
            vector<int> v;

            for(int i{};i<m;++i){
                v.push_back(left[i][j]);
            }

            ret = max(ret,largestRectangleArea(v));
        }
 
        return ret;
    }
};

37. 94. 二叉树的中序遍历

// 二叉树的遍历
class Solution {
public:
    vector<int> result;

    void inorder(TreeNode* root){
        if(!root) return;

        inorder(root->left);
        result.push_back(root->val);
        inorder(root->right);
    }

    vector<int> inorderTraversal(TreeNode* root) {
        inorder(root);
        return result;
    }
};

38. 96. 不同的二叉搜索树

// 动态规划
class Solution {
public:
	// dp[3],就是元素1的头节点搜索树的数量+元素2为头节点搜索树的数量+元素3为头节点搜索树的数量
	// dp[3] =  dp[2] * dp[0] + dp[1] * dp[1] + dp[0] * dp[2]
    int numTrees(int n) {
    	// dp[i]:1到i为节点组成的二叉搜索树的个数为dp[i]
        vector<int> dp(n+1);
        dp[0] = 1;
        for(int i{1};i<=n;++i){
            for(int j{1};j<=i;++j){
            	// dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量],j相当于是头节点的元素，从1遍历到i为止
                dp[i] += dp[j-1]*dp[i-j];
            }
        }

        return dp[n];
    }
};

39. 98. 验证二叉搜索树

// 二叉树的遍历
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> v;

    bool recursive(TreeNode* root){
        if(!root) return true;

        recursive(root->left);
        v.push_back(root->val);
        recursive(root->right);

        return true;
    }
    bool isValidBST(TreeNode* root) {
        recursive(root);

        for(int i{};i<v.size();++i){
            if(i && v[i-1] >= v[i]){
                return false;
            }
        }
        return true;
    }
};

40. 101. 对称二叉树

// 二叉树递归
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    bool recursive(TreeNode* left,TreeNode* right){
        if(!left && !right) return true;
        else if(left && !right) return false;
        else if(!left && right) return false;

        if(left->val != right->val) return false;
        
        bool flag = recursive(left->left, right->right);
        bool flag1 = recursive(left->right, right->left);

        return flag && flag1;
    }
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;

        return recursive(root->left,root->right);
    }
};

41. 102. 二叉树的层序遍历

// 二叉树的遍历
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<vector<int>> result;

    vector<vector<int>> levelOrder(TreeNode* root) {
        if(!root) return {};

        queue<TreeNode*> q;
        q.push(root);

        while(!q.empty()){
            int n = q.size();
            vector<int> v1;
            for(int i{};i<n;++i){
                TreeNode* node = q.front();
                q.pop();

                v1.emplace_back(node->val);

                if(node->left) q.push(node->left);
                if(node->right) q.push(node->right);
            }

            result.push_back(v1);
        }
        return result;
    }
};

42. 104. 二叉树的最大深度

// 树的递归
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(!root) return {};

        return max(maxDepth(root->left),maxDepth(root->right)) + 1;
    }
};

43. 105. 从前序与中序遍历序列构造二叉树

// 树的遍历
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* recursive(vector<int>& inorder, vector<int>& preorder){
    	// 递归终止条件
        if(preorder.size() == 0) return {};
		// 后续遍历的最后一个是根节点
        TreeNode* root = new TreeNode(preorder[0]);
		
		// 在中序中找到根节点，左边的就是左子树、右边的数据就是右子树
        int index{};
        for(int i{};i<inorder.size();++i){
            if(inorder[i] == preorder[0]) index = i;
        }
        // 左闭右开的区间，然后拆分左右子树再次进行递归
        vector<int> leftInorder(inorder.begin(),inorder.begin() + index);
        vector<int> rightInorder(inorder.begin() + index +1,inorder.end());

        vector<int> leftPreorder(preorder.begin()+1,preorder.begin()+1+ leftInorder.size());
        vector<int> rightPreorder(preorder.begin()+1+ leftInorder.size(),preorder.begin()+1+ leftInorder.size() + rightInorder.size());

        root->left = recursive(leftInorder,leftPreorder);
        root->right = recursive(rightInorder,rightPreorder);

        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        if(preorder.size() ==0 || inorder.size() == 0) return {};

        return recursive(inorder,preorder);
    }
};

44. 114. 二叉树展开为链表

// 问题转化为寻找当前节点的前驱节点
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void flatten(TreeNode* root) {
        if(!root) return;
        // 寻找当前节点的前驱节点
        TreeNode* cur = root;
        while(cur){
            while(cur->left){
                // 当前节点的左节点
                TreeNode* next = cur->left;
                TreeNode* pre  = next;
                // 得到前驱节点
                while(pre->right){
                    pre = next->right;
                }

                pre->right = cur->right;
                cur->left = nullptr;
                cur->right = next;
            }
            cur = cur->right;
        }
    }
};

45. 121. 买卖股票的最佳时机

// 贪心
class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int result{};
        // 记录最小值
        int minValue = prices[0];
        for(int i{1};i<prices.size();++i){
        	// 贪心获取一次买卖的最大利润
            result = max(result,(prices[i] - minValue));
            minValue = min(minValue,prices[i]);
        }
        return result;
    }
};

46. 124. 二叉树中的最大路径和

// 递归求解（从根节点向上求解）
class Solution {
private:
    int maxSum = INT_MIN;

public:
    int maxGain(TreeNode* node) {
        if (node == nullptr) {
            return 0;
        }
        
        // 递归计算左右子节点的最大贡献值
        // 只有在最大贡献值大于 0 时，才会选取对应子节点
        int leftGain = max(maxGain(node->left), 0);
        int rightGain = max(maxGain(node->right), 0);

        // 节点的最大路径和取决于该节点的值与该节点的左右子节点的最大贡献值，因为路径不是自上而下的遍历
        int priceNewpath = node->val + leftGain + rightGain;

        // 更新答案
        maxSum = max(maxSum, priceNewpath);

        // 返回节点的最大贡献值
        return node->val + max(leftGain, rightGain);
    }

    int maxPathSum(TreeNode* root) {
        maxGain(root);
        return maxSum;
    }
};

47. 128. 最长连续序列

// 哈希表+模拟
class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> num_set;
        for (const int& num : nums) {
            num_set.insert(num);
        }

        int longestStreak = 0;

        for (const int& num : num_set) {
        	// 核心关键是这个内层的跳过的逻辑
        	// 枚举的数 x 一定是在数组中不存在前驱数 x-1
            if (!num_set.count(num - 1)) {
                int currentNum = num;
                int currentStreak = 1;

                while (num_set.count(currentNum + 1)) {
                    currentNum += 1;
                    currentStreak += 1;
                }

                longestStreak = max(longestStreak, currentStreak);
            }
        }

        return longestStreak;           
    }
};

48. 136. 只出现一次的数字

// 位运算
// 异或运算的性质
// 1.任何数和0做异或运算，结果仍是原来的数
// 2.任何数和自己异或结果是0
// 3.异或运算满足交换律和结合律
class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int n = nums.size();

        int result{nums[0]};

        for(int i{1};i<n;++i){
            result ^= nums[i];
        }

        return result;
    }
};

49. 139. 单词拆分

// 动态规划、完全背包问题
class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> unSet(wordDict.begin(),wordDict.end());
        int n = s.size();
        // 1.确定dp数组以及下标的含义
        // dp[i]为true表示 字符串从1-i可以被拆分成多个单词
        vector<int> dp(n+1);
        dp[0] = true;

        for(int j = 1;j<=n;++j){ // 遍历背包
            for(int i{};i<=j;++i){ // 遍历物品
                string str = s.substr(i,j-i);

                if(dp[i] && unSet.find(str) != unSet.end()){
                    dp[j] = true;
                }
            }
        }
        return dp[n];
    }
};

50. 141. 环形链表

// 双指针
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode *slow = head;
        ListNode *fast = head;

        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;

            if(slow == fast){
                return true;
            }
        }

        return false;
    }
};

51. 142. 环形链表 II

// 双指针 + 数学
// 核心：a=c+(n−1)(b+c) 的等量关系，我们会发现：从相遇点到入环点的距离加上 n-1n−1 圈的环长，恰好等于从链表头部到入环点的距离
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(!head || !head->next || !head->next->next) return {};

        ListNode* slow = head;
        ListNode* fast = head;

        while(fast && fast->next){
            slow = slow->next;
            fast = fast->next->next;

            if(slow == fast){
                break;
            }
        }

        if(slow != fast) return{};

        slow = head;

        while(slow != fast){
            slow = slow->next;
            fast = fast->next;
        }

        return slow;
    }
};

52. 146. LRU 缓存

// LRU(最近最少使用缓存)
// hashmap建立索引、list创建最近最少使用淘汰机制
class LRUCache {
public:
    LRUCache(int capacity) {
        size = capacity;
    }
    
    int get(int key) {
        if(m.find(key) == m.end()){
            return -1;
        }
        l.splice(l.begin(),l,m[key]);
        return m[key]->second;
    }
    
    void put(int key, int value) {
        if(m.find(key) != m.end()){
            l.splice(l.begin(),l,m[key]);
            m[key]->second = value;
            return;
        }

        if(size == l.size()){
            auto dKey = l.back().first;
            l.pop_back();
            m.erase(dKey);
        }

        l.push_front({key,value});
        m[key] = l.begin();
    }

private:
    list<pair<int,int>> l;
    unordered_map<int,list<pair<int,int>>::iterator> m;
    int size{};
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

53. 148. 排序链表

// 链表

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        vector<int> v;

        ListNode* cur = head;

        while(cur){
            v.push_back(cur->val);
            cur = cur->next;
        }

        sort(v.begin(),v.end());
        cur = head;
        for(int i{};i<v.size();++i){
            cur->val = v[i];
            cur = cur->next;
        }

        return head;
    }
};

54. 152. 乘积最大子数组

// 动态规划
class Solution {
public:
    int maxProduct(vector<int>& nums) {
        int ans{INT_MIN},n = nums.size();

        if(1==n) return nums[0];

        vector<int> dpMax(n);
        vector<int> dpMin(n);

        dpMax[0] = nums[0];
        dpMin[0] = nums[0];
        ans = nums[0];
        for(int i = 1;i<n;++i){
            dpMax[i] = max(nums[i],max(nums[i]*dpMax[i-1],nums[i]*dpMin[i-1]));
            dpMin[i] = min(nums[i],min(nums[i]*dpMax[i-1],nums[i]*dpMin[i-1]));
            ans = max(ans,dpMax[i]);
        }

        return ans;
    }
};

55. 155. 最小栈

// 栈
// 使用两个栈，专门维护一个储存最小值的栈
class MinStack {
public:
    MinStack() {

    }
    
    void push(int val) {
        if(s2.empty() || val <= s2.top()) s2.push(val);
        s1.push(val);
    }
    
    void pop() {
        if(s1.empty() && s2.empty()) return;
        if(s1.top() == s2.top()) s2.pop();
        s1.pop();
    }
    
    int top() {
        if(s1.empty()) return -1;
        return s1.top();
    }
    
    int getMin() {
        if(s2.empty()) return -1;
        return s2.top();
    }
private:
    stack<int> s1;
    stack<int> s2;
};

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack* obj = new MinStack();
 * obj->push(val);
 * obj->pop();
 * int param_3 = obj->top();
 * int param_4 = obj->getMin();
 */

56. 160. 相交链表

// 链表+哈希表
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
        unordered_set<ListNode*> unS;

        while(headA){
            unS.insert(headA);
            headA = headA->next;
        }

        while(headB){
            if(unS.find(headB)!=unS.end()) return headB;
            headB = headB->next;
        }

        return {};
    }
};

57. 169. 多数元素

// 哈希表
class Solution {
public:
    int majorityElement(vector<int>& nums) {
        unordered_map<int,int> mp;

        for(int num : nums) {
            mp[num]++;
            if(mp[num] > nums.size()/2) return num;
            
        }

        return -1;
    }
};

58. 198. 打家劫舍

// 动态规划
class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        // 1.dp数组以及下标定义
        // dp[i][0] 第i-1天不偷窃，最多可以偷窃的金钱的数目为dp[i][0]
        // dp[i][1] 第i-1天偷窃
        vector<vector<int>> dp(n,vector<int>(2));

        dp[0][0] = 0;
        dp[0][1] = nums[0];

        int result{};

        for(int i{1};i<n;++i){
            dp[i][0] = max(dp[i-1][0],dp[i-1][1]);
            dp[i][1] = max(dp[i-1][0],dp[i-1][0] + nums[i]);
        }

        return max(dp[n-1][0],dp[n-1][1]);
    }
};

59. 200. 岛屿数量

// dfs广度有限遍历
class Solution {
public:
    void dfs(int i,int j,vector<vector<char>>& grid){
        if(min(i,j) < 0 || i>=grid.size() || j >= grid[0].size()) return;
		
		// 如果是水或者已经被访问过，即是其它的小岛的组成部分就跳过
        if(grid[i][j] == '0' || grid[i][j] == '2') return;
        grid[i][j] = '2';
		// 广度优先遍历
        for(int d{};d<4;++d){
            dfs(i+dx[d],j+dy[d],grid);
        }
    }
    int numIslands(vector<vector<char>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        int count{};
		// 依次进行广搜
        for(int i{};i<m;++i){
            for(int j{};j<n;++j){
                if(grid[i][j] == '1'){
                    dfs(i,j,grid);
                    count++;
                }
            }
        }

        return count;
    }

private:
    int dx[4]{1,0,-1,0};
    int dy[4]{0,-1,0,1};
};

60. 206. 反转链表

// 双指针 + 画图

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        if(!head) return {};

        ListNode* pre = nullptr;
        ListNode* cur = head;

        while(cur){
            ListNode* node = cur->next;
            cur->next = pre;
            pre = cur;
            cur = node;
        }

        return pre;
    }
};

61. 207. 课程表

// 拓扑排序+dfs+bfs
class Solution {
private:
	// 表示有向有环图
    vector<vector<int>> edges;
    // 记录每个节点的入度
    vector<int> indeg;

public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        edges.resize(numCourses);
        indeg.resize(numCourses);
        for (const auto& info: prerequisites) {
            edges[info[1]].push_back(info[0]);
            ++indeg[info[0]];
        }

        queue<int> q;
        for (int i = 0; i < numCourses; ++i) {
            if (indeg[i] == 0) {
                q.push(i);
            }
        }

        int visited = 0;
        while (!q.empty()) {
            ++visited;
            int u = q.front();
            q.pop();
            for (int v: edges[u]) {
                --indeg[v];
                if (indeg[v] == 0) {
                    q.push(v);
                }
            }
        }

        return visited == numCourses;
    }
};