目录
一、集合概述
Python中的集合类型数据结构是将各不相同的不可变数据对象无序地集中起来的容器,就像是将值抽离,仅存在键的字典。类似于字典中的键,集合中的元素都是不可重复的,并且是属于不可变类型,元素之间没有排列顺序。集合的这些特性,使得它独立于序列和映射类型之外,Python中的集合类型就相当于数学集合论中所定义的集合,人们可以对集合对象进行数学集合运算(并集、交集、差集等)。
二、集合的创建
若按数据结构对象是否可变来分,集合类型数据结构包括可变集合与不可变集合。
(一)可变集合
可变集合对象是可变的,可对其进行元素的增添、删除等处理,处理结果直接作用在对象上。使用花括号可以创建可变集合,这里与创建字典不同,传入的不是键值对,而是集合元素,注意,传入的元素对象必须是不可变的,即不能传入列表、字典甚至可变集合等。另外,可变集合的set函数能够将数据结构对象转换为可变集合类型,即将集合元素存储为一个列表或元组,再使用set函数转换为可变集合。在创建时,无须担心传入的元素是否重复,因为结果会将重复元素删除。若需要创建空集合,只能使用set 函数日不传入任何参数进行创建,代码如下。
# 使用花括号创建可变集合
set1={'A','C','D','B','A','B'}
set1
# 使用函数set()创建可变集合
set2=set([2,3,1,4,False,2.5,'one'])
set2
# 创建空可变集合
empty_set=set()
empty_set
type(empty_set)注意:
(1)set函数创建可以把其他数据类型转变为集合,并且自动去重:
list=[1,2,3,1,6,2,5]
exset1=set(list) # 把列表转换为集合,注意set函数只允许有一个可迭代对象作为参数!
print(exset1) # 输出结果: {1, 2, 3, 5, 6}(2)创建空集合只能使用set函数,而空的花括号创建的是空字典!
exset2=set() # 空集合,可以利用type(exset2)查看
exset3={} # 本想创建空集合,结果创建的却是空字典,可以利用type(exset3)查看(二)不可变集合
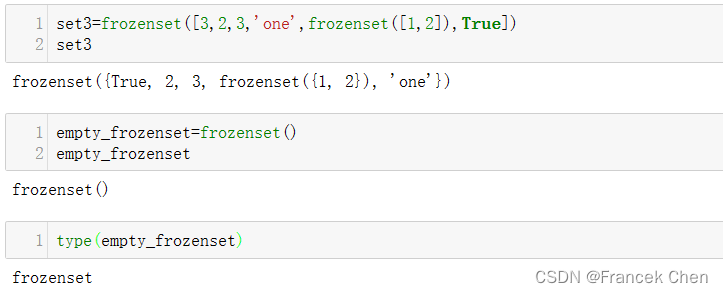
不可变集合对象属于不可变数据类型,不能对其中的元素进行修改处理。创建不可变集合的方法是使用frozenset函数。它与set函数用法一样,不同的是得出的结果是一个不可变集合。注意,元素必须为不可变数据类型。使用不可变集合作为元素,当frozenset函数不传入任何参数时,则会创建一个空不可变集合,代码如下。
# 使用函数frozenset()创建不可变集合
set3=frozenset([3,2,3,'one',frozenset([1,2]),True])
set3
# 创建空不可变集合
empty_frozenset=frozenset()
empty_frozenset
type(empty_frozenset)三、可变集合用法
1、集合主要用于元素去重、成员关系测试(in/not in)、删除数据项等。
2、用于元素去重,例如可以把含有重复元素的列表list1通过list(set(list1)的方式实现自动去重,当然list1的元素一定是不可变类型才能用set函数转换。
3、因为元素无序,因此:
(1)不能用索引或下标访问单个元素,只能整体打印输出;
(2)因为不能用索引或下标访问单个元素,因此无法对可变集合中的元素进行值的修改,只能增删元素;
(3)输出的顺序可以与创建时的顺序不同。
4、集合元素可迭代,可以用于for循环:
str = '知之为知之不知为不知'
S = {char for char in str} # 使用了集合推导式来快速创建集合对象
S
{'不', '为', '之', '知'}
for i in S:
print(i, end="")
不为之知 四、集合运算
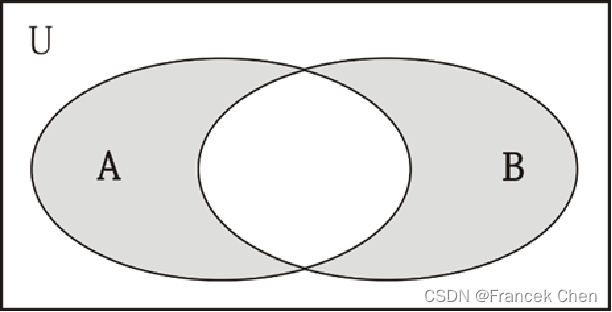
(一)并集
由属于集合A或集合B的所有元素组成的集合,称为集合A和B的并集,数学表达式为:
A∪B={x|x∈A或x∈B}
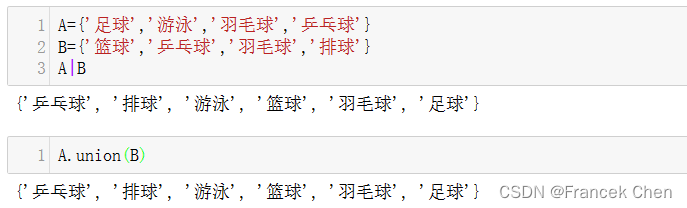
在Python中可以使用符号“|”或者集合方法union函数来得出两个集合的并集。
A={'足球','游泳','羽毛球','乒乓球'}
B={'篮球','乒乓球','羽毛球','排球'}
A|B # 使用符号’|’获取并集
A.union(B) # 使用集合方法union函数获取并集(二)交集
同时属于集合A和B的元素组成的集合,称为集合A和B的交集,数学表达式为:
A∩B={x|x∈A且x∈B}
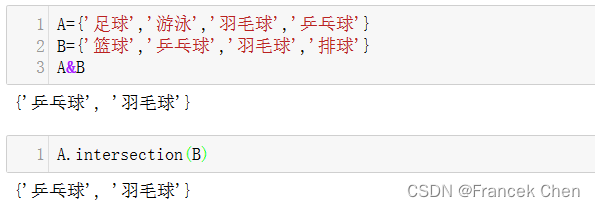
可以利用符号“&”或者集合方法intersection函数来获取两个集合对象的交集。
A={'足球','游泳','羽毛球','乒乓球'}
B={'篮球','乒乓球','羽毛球','排球'}
A&B # 使用符号’&’获取交集
A.intersection(B) # 使用集合方法intersection函数获取交集
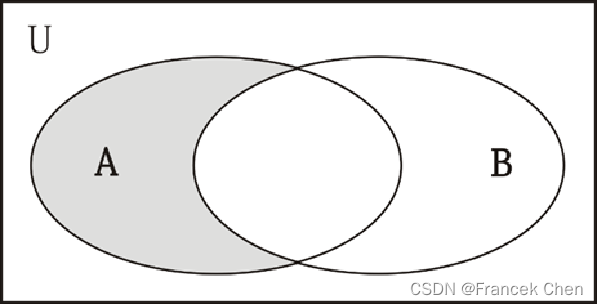
(三)差集
属于集合A而不属于集合B中的元素所构成的集合,称为集合A减集合B,数学表达式为:
A-B={x|x∈A,x∉B}
这个集合也称为集合A与集合B的差集。反过来,也有差集B-A={x|x∈B,x∉A}。在Python中可以简单地使用减号“-”来得到相应的差集,或者可以通过集合方法difference函数来实现。
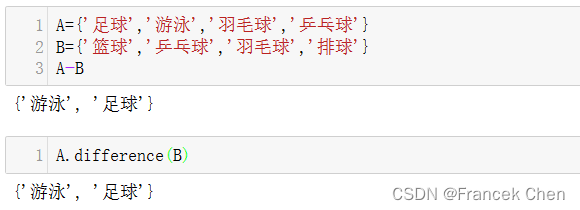
A={'足球','游泳','羽毛球','乒乓球'}
B={'篮球','乒乓球','羽毛球','排球'}
A-B # 使用减号“-”来获取差集
A.difference(B) # 使用集合方法difference函数获取差集
(四)异或集
属于集合A或集合B,但不同时属于集合A和B的元素所组成的集合,称为集合A和B的异或集,其相当(A∪B)-(A∩B)。利用符号“^”或者集合方法symmetric_difference函数即可求出两个集合对象的异或集。
A={'足球','游泳','羽毛球','乒乓球'}
B={'篮球','乒乓球','羽毛球','排球'}
A^B # 获取异或集
A.symmetric_difference(B) # 使用集合方法symmetric_difference函数获取异或集五、集合常用函数和方法
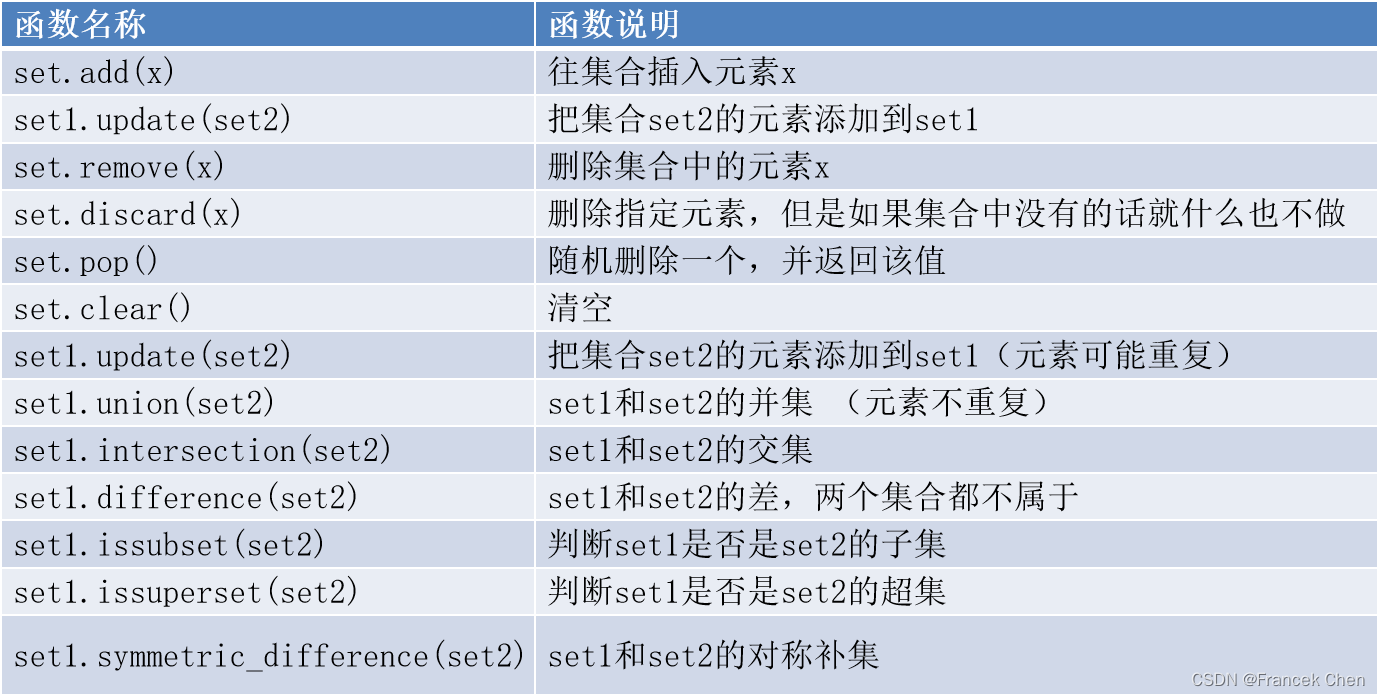
集合类型数据结构分为可变集合与不可变集合,与其他类型数据对象一样,对于可变集合对象,也可以进行元素的增添、删除、查询等处理,相关常用函数和方法如下表所示。
set4={'red','green','blue','yellow'}
set4_copy=set4.copy() # 创建一个集合副本对象
others={'black','white'}
# 可变集合增添元素
set4.add('orange') # 使用集合方法add()函数增添元素
set4.update(others) # 使用集合方法update()函数合并两个集合
set4
# 可变集合删除元素
set4.pop() # 使用pop()函数从集合中抽离出一个元素
set4 # 查看抽离元素后的集合内容
set4.remove('yellow') # 使用remove()删除指定元素
set4_copy.clear() # 使用clear()将副本集合内容清空
set4_copy
# 使用in查看集合是否包含指定元素
'green' in set4
# 使用len( )函数获取集合元素个数
len(set4)