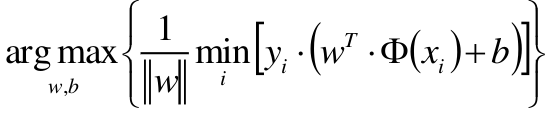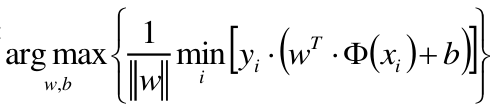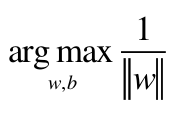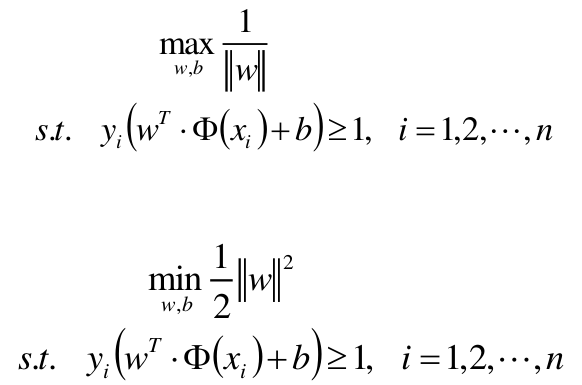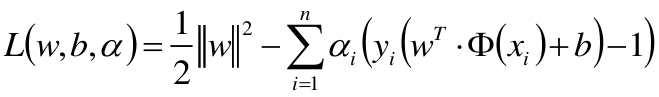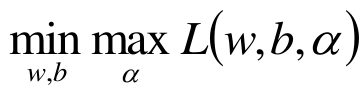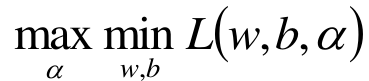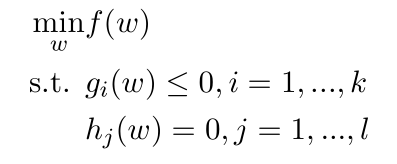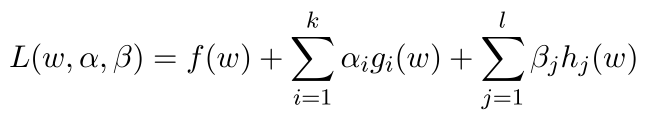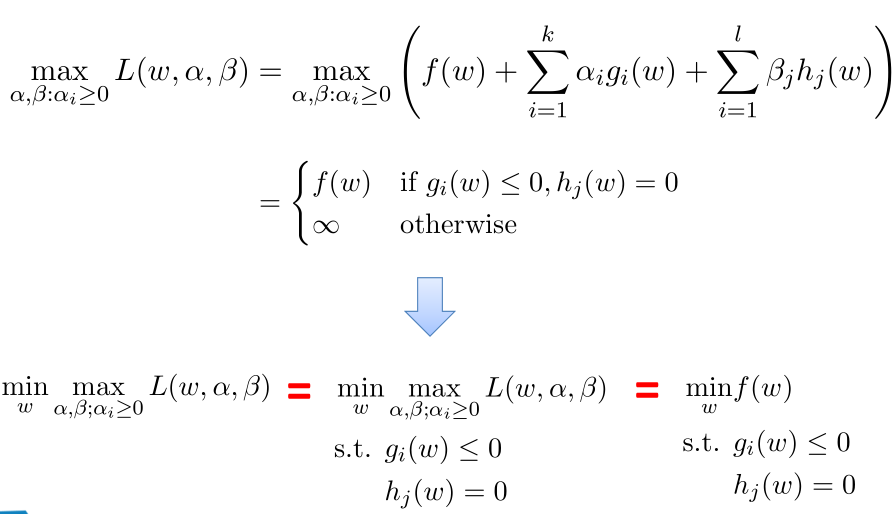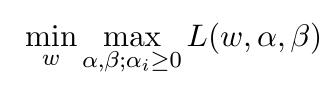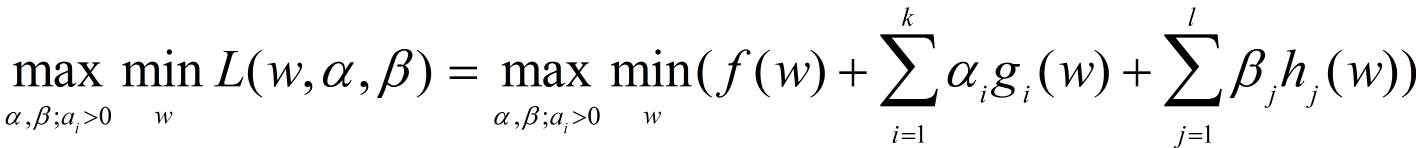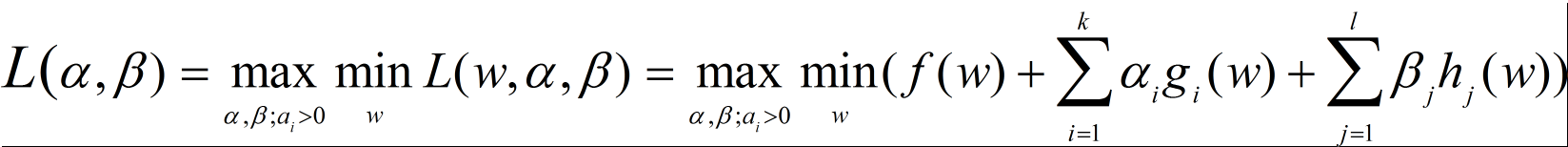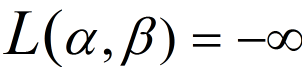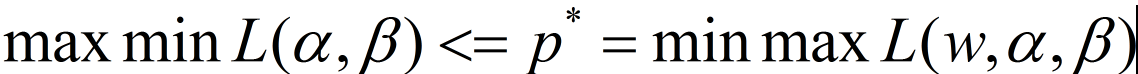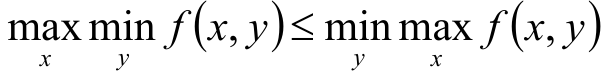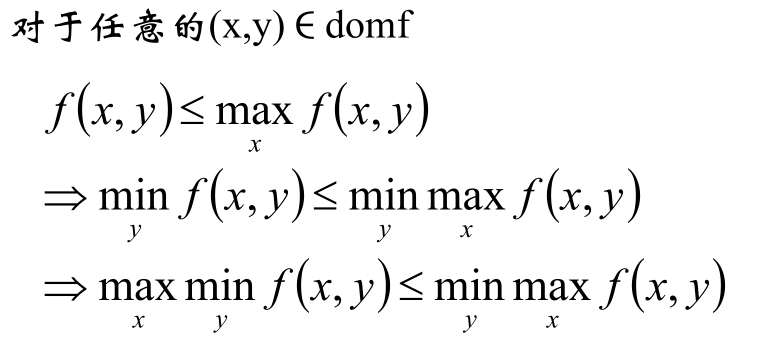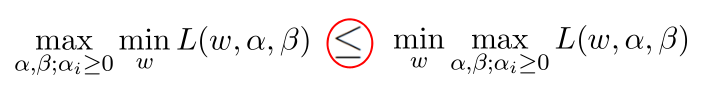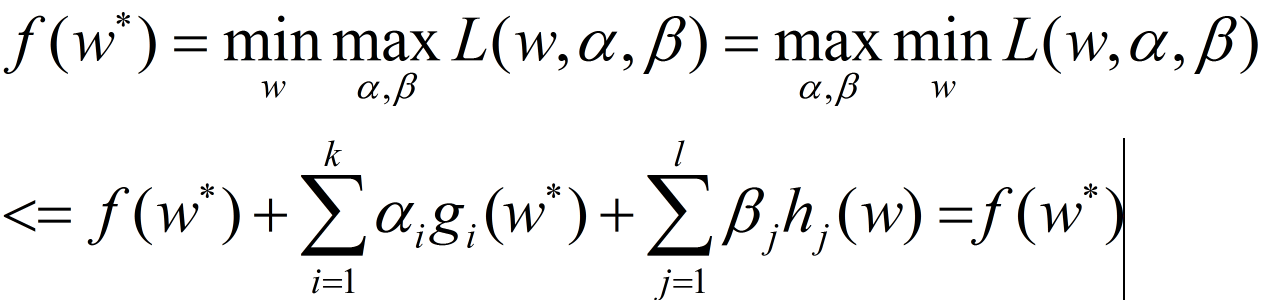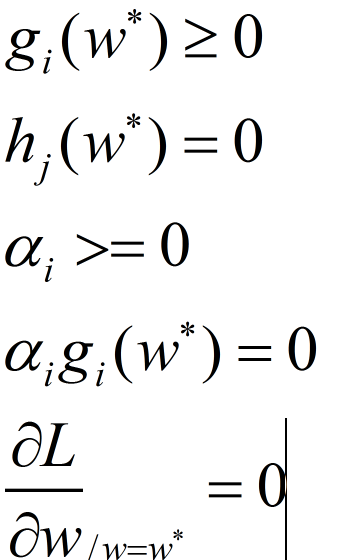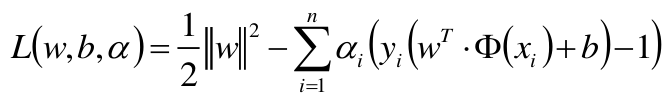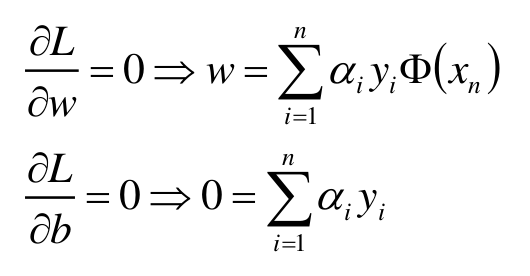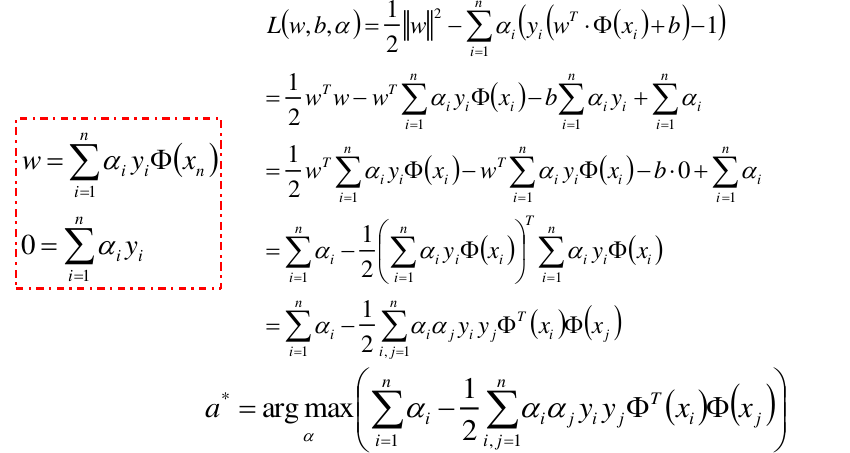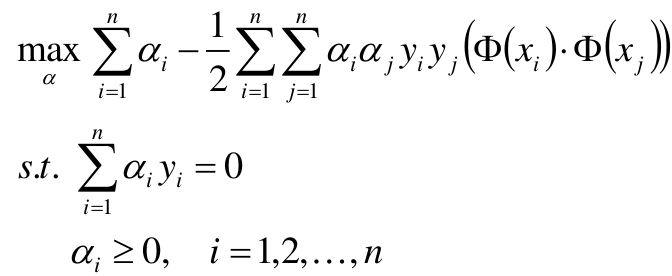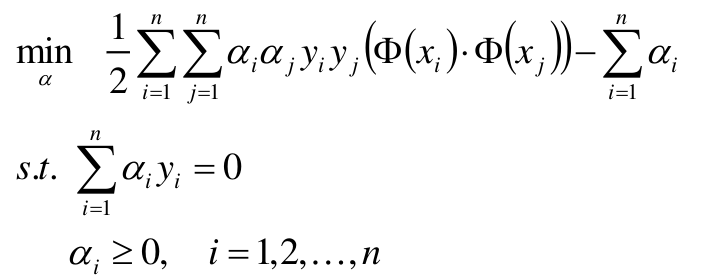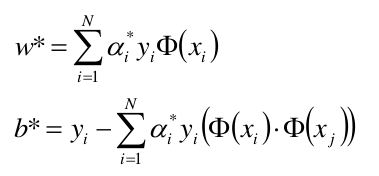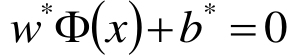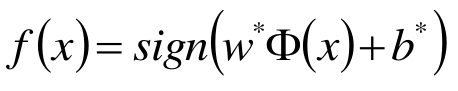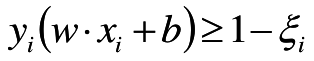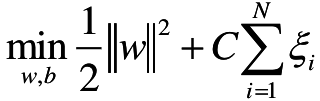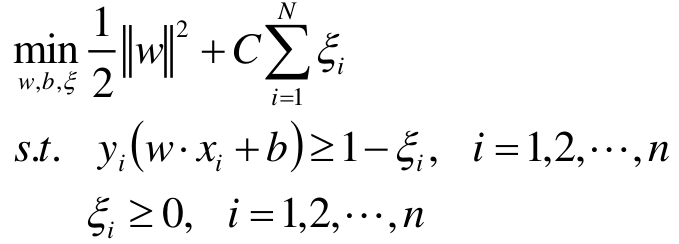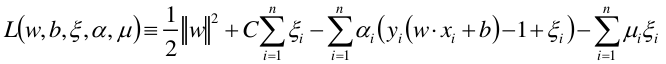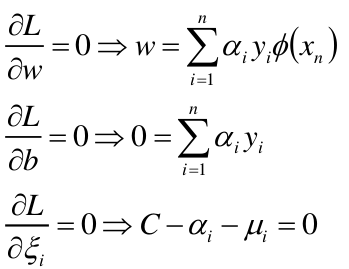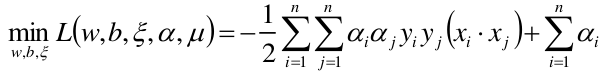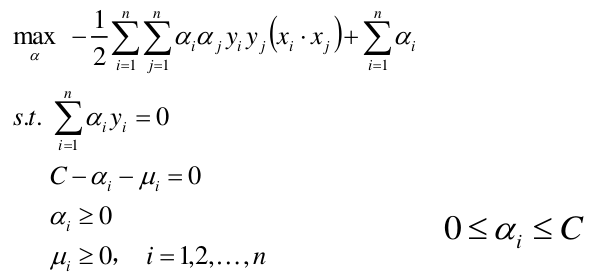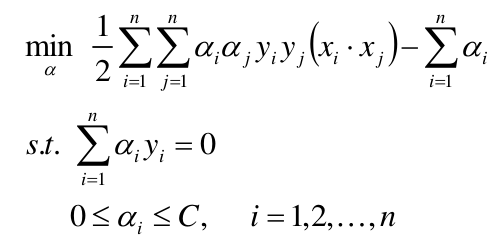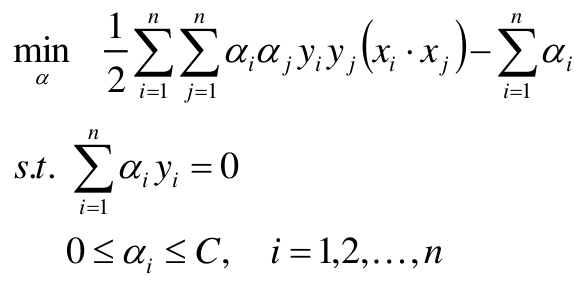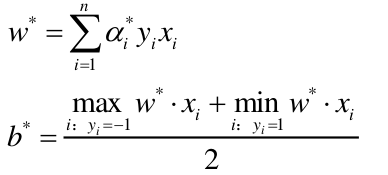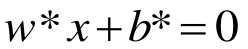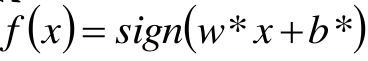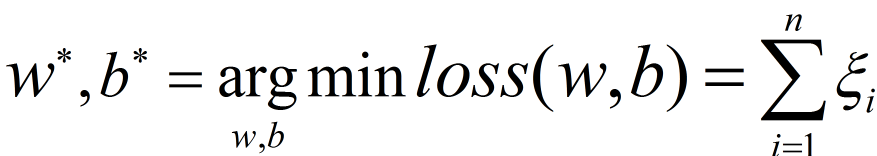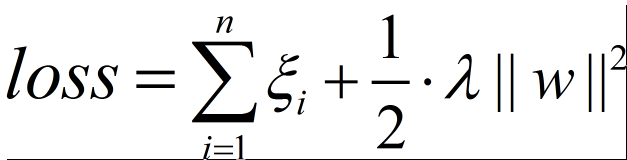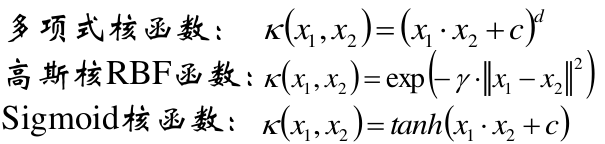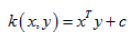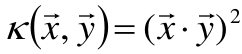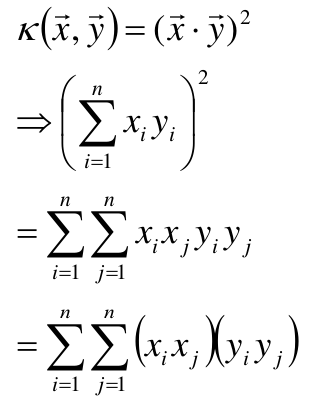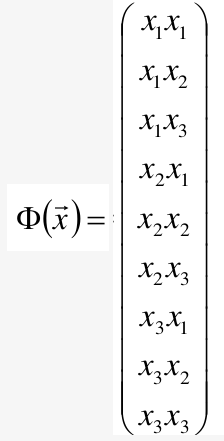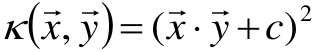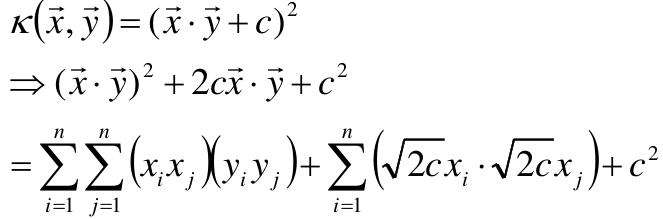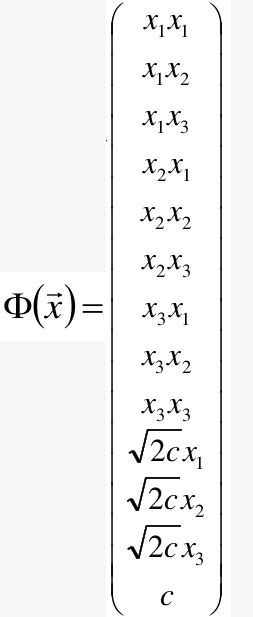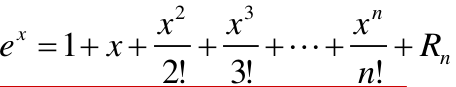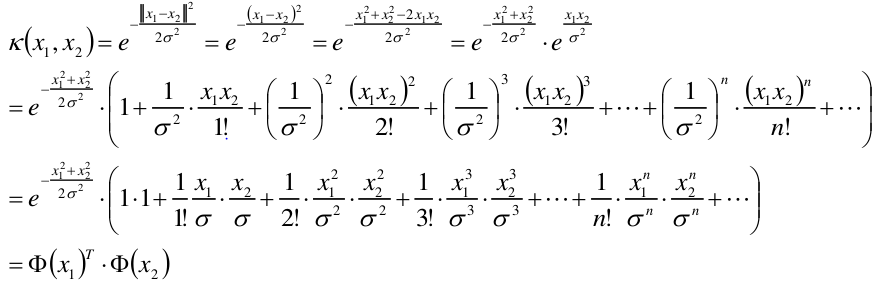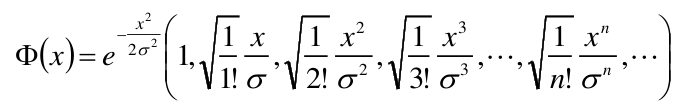本篇博文将详细总结机器学习里面一个非常重要但又非常难以理解的一个算法模型SVM。SVM我之前一直没有弄的很明白，在总结本篇博文时，一定要将其弄得清清楚楚。

将沿着以下几个主题来进行总结：

线性可分支持向量机（硬间隔最大化hard margin maximization）

定义

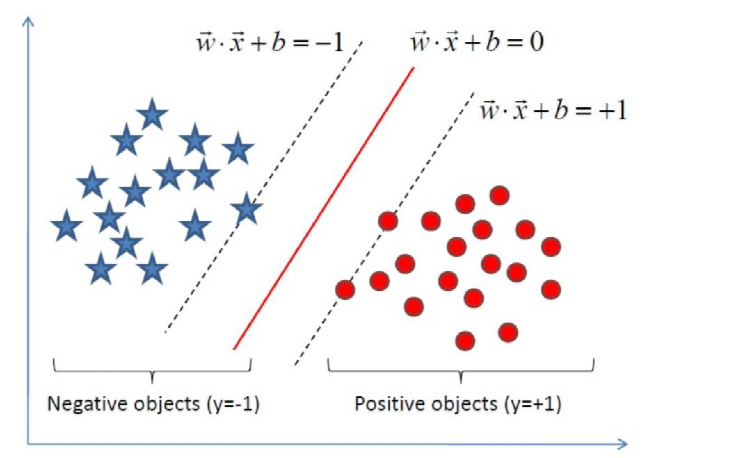
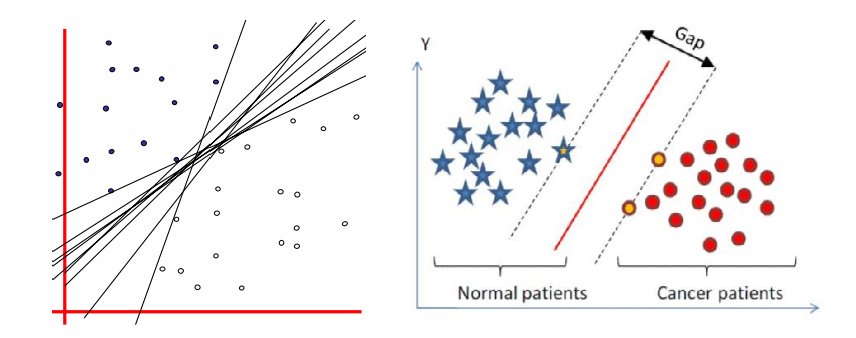
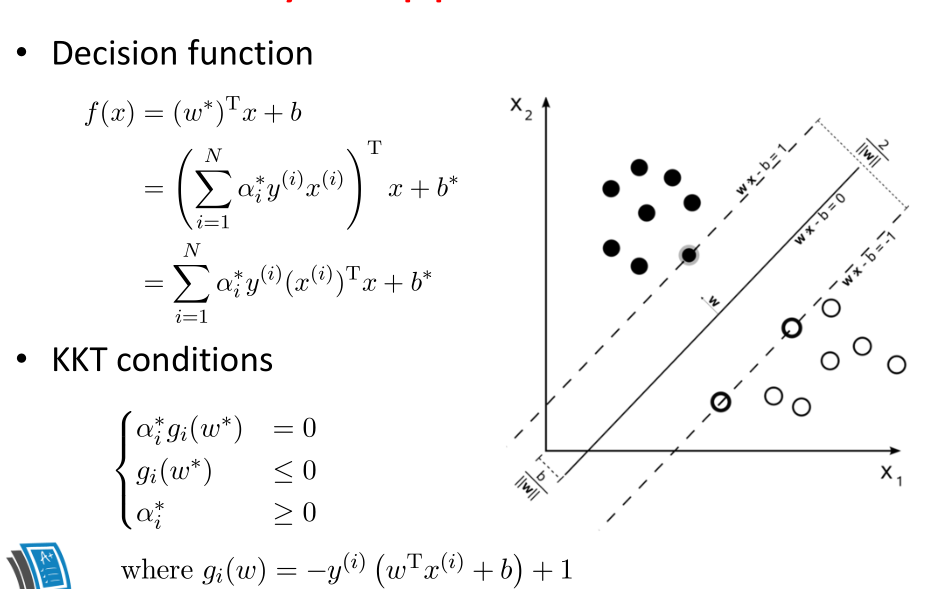
上图就形象的说明什么是线性可分支持向量机，利用SVM对样本进行分类得到分割超平面（实线）和边界的两条虚线，并且分割后可以使得没有样本点落在两条虚线之内，那么这就是线性可分的。我们把落在边界，也就是两条虚线之上的样本点称为支持向量（support vector）。

给定线性可分训练数据集，通过 间隔最大化得到的分离超平面为 :

$$y(x)=W^T\Phi (x)+b$$

相应的分类决策函数，$f(x)=sign(W^T\Phi (x)+b)$，该决策函数称为线性可分支持向量机。

$\Phi (x)$是某个确定的特征空间转换函数（即核函数），它的作用是将$x$映射到(更高的)维度。在线性可分支持向量机中$\Phi (x)=x$，那么如何选取这个分割超平面呢？

分割超平面的思考

假设给定一个特征空间上的训练数据集 $T=(x_1,y_1),(x_2,y_2),...,(x_N,y_N)$，其中$x_i\in R_n,y_i\in +1,-1,i=1,2,...,N$，$x_i$ 为第$i$ 个实例（若$n>1,x_i$ 为向量）；

$y_i$为 $x_i$的类标记；当$y_i=+1$时，称$x_i$ 为正例；当$y_i=-1$ 时，称$x_i$ 为负例；$(x_i,y_i)$ 称为一个样本点。

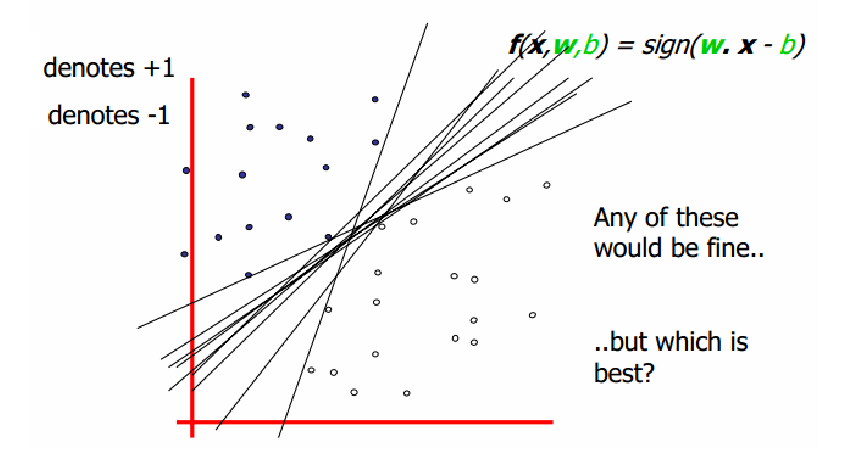
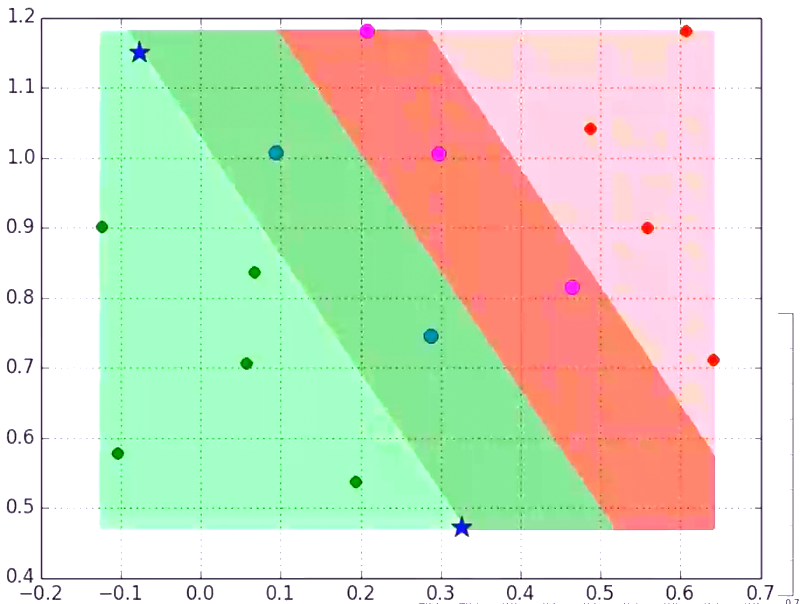
上图中，存在多条分割线能将正负样本分类，那么哪一条是最好的分割线呢？直观上看应该找最中间的那条直线，因为该超平面对训练样本的局部扰动的容忍性最好。换言之，这个划分超平面所产生的分类结果是最鲁棒的，对未见实例的泛化性最强。

我们先对这条分割线进行向量化的表示，例如$y=2x-1$可以表示成 $y(X)=y-2x+1$，其中$x,y$ 是自变量（特征），$y(X)$ 是对应的计算结果，大于 $0$或者小于$0$ 。可以进行向量化的表示:$y(X)=\overrightarrow{W}\cdot \overrightarrow{X}+b$那么这里$\overrightarrow{W}=(1,-2);\overrightarrow{X}=(y,x)$

整理符号：
分割平面：$$y(x)=w^T\Phi (x)+b$$

训练集：$x_1,x_2,...,x_n$

目标值：$y_1,y_2,...,y_n$

新数据的分类：$sign(y(x))$

由此可推出：

$$\{\begin{array}{cc}y(x_i)>0\iff y_i=+1& \\ y(x_i)<0\iff y_i=-1& \end{array}\Rightarrow y_i\cdot y(x_i)>0$$

注：$y(x_i)$表示代入分割超平面方程所得的结果；$y_i$表示样本所对应的类别标签（这里是以二分类为例，正类用+1表示，负类用-1表示）

函数距离

在超平面$\overrightarrow{W}\cdot \overrightarrow{X}+b=0$确定的情况下，通过观察$\overrightarrow{W}\cdot \overrightarrow{X}+b$ 符号与类标记 $y_i$的符号是否一致可判断分类是否正确，所以，可以用$y_i\cdot (\overrightarrow{W}\cdot \overrightarrow{X}+b)$的正负性来判定或表示分类的正确性。正号即分类正确，反正分类结果错误。于此，我们便引出了函数距离（functional margin）的概念。

$$\gamma =y_i(\overrightarrow{W}\Phi (x)+b)=y_i\cdot y_i(x_i)$$

我们知道一条直线或者一个分割超平面，**其同步的放大或缩小所有参数，其直线或面（经过的点）并不发生改变。**显然当成倍的变化$W,b$ 时，函数距离也在成倍变化，不合理，故这样定义距离还远远不够。

几何距离

$W,b$ 等比例缩放，则$\gamma$ 值同样缩放，从而：

$$\frac{y_i\cdot y(x_i)}{\parallel W\parallel }=\frac{y_i(\overrightarrow{W}\Phi (x)+b)}{\parallel W\parallel }$$

显然此时无论参数$W,b$ 如何变化，其确定点到直线的距离都不发生改变。

最大间隔分离超平面

我们的目的就是要在所有可能的$W,b$ 中，其中每一个可能的$w,b$都能确定一条分割超平面，计算出每个分割超平面距离正负样本的最短距离，然后在这些最短距离中找出最大距离 对应的那个$w,b$。那么这个$w,b$ 所确定的超平面也就是最优分割超平面。上面讲的最大最小距离指的都是几何距离。

故目标函数：

建立目标函数：
分割平面：

$$y=w^T\Phi (x)+b$$

总可以通过等比例缩放$w，b$ 的方法，使得两类点的函数距离 都满足$|y|\ge 1$

即约束条件：

$$y_i\cdot (w^T\Phi (x)+b)>=1$$

原目标函数：

新目标函数：

拉格朗日乘子法：

原问题是极小极大问题：

原始问题的对偶问题，是极大极小问题：

关于最小最大问题转成其对偶形式最大最小问题，里面涉及到凸优化相关知识，这里我们不过多探讨凸优化，只讲下其相关结论。

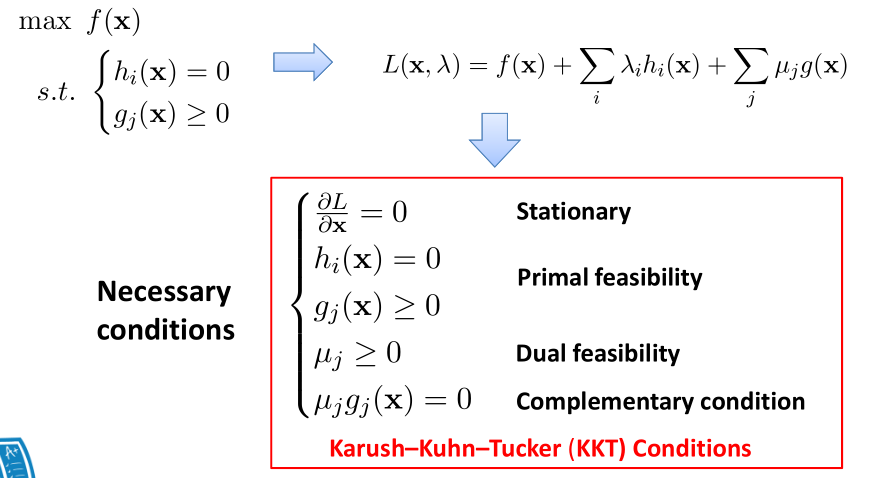
凸优化相关结论

在多重等式或不等式约束下：

原问题：
约束条件如果是大于等于,前面添加负号总能变换成小于等于号。

广义的拉格朗日：

min-max问题：

注：上面先求最大值，然后在最大值 $[f(w),无穷]$ 里面求最小值。其推导过程证明了拉格朗日的min-max问题最后结果和原问题在约束条件下的最优结果是一致的。

原始问题（min-max问题）：

对偶问题（max-min问题）：

显然，固定$w$，那么$max-min$就是关于$\alpha ,\beta$的函数，

这个$L(\alpha ,\beta )$即为对偶函数。

若没有下确界，定义：

根据定义，若有下确界，显然有：对$\forall \alpha >0,\forall \beta$，若原优化问题有最优值$p\ast =minf(w)$ 在约束条件$（g<=0,h=0）$下，则在上面的约束条件下（g<=0,h=0）得：
应该是小于等于

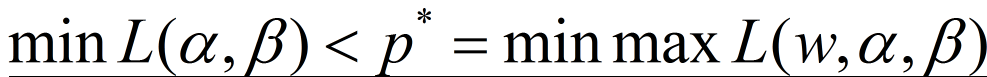
那么就可得：

证明：

注：如果一个函数f1小于另外一个函数f2，那么就意味着函数f1在定义域内的所有取值（不论是最大取值还是最小取值）都小于f2在定义域内的任意取值。

即：

强对偶条件
若要对偶函数的最大值即为原问题的最小值，即要上面等号成立，考察需要满足的条件：
我们假定 $w^{\ast }$为原问题的最优解，那么也就是其拉个朗日$min-max$ 的最优解。

显然要使上式成立，需要满足以下几个条件：

这就是所谓的KKT条件，满足KKT条件，则min-max问题等价与max-min问题。

SVM的拉格朗日函数

其中$-{\sum }_{i=1}^n{\alpha }_i(y_i(w^T\cdot \Phi (x_i)+b)-1)<=0$

将拉格朗日函数$L(w,b,a)$ 分别对$w，b$求偏导 并令其为 $0$ ：

***上面所求出的w即为kkt条件中的 KaTeX parse error: Undefined control sequence: \* at position 3: W^\̲*̲***。

计算拉格朗日函数的对偶函数

继续求$mi{n}_{w,b}L(w,b,\alpha )$对 $\alpha$的极大

显然所求出来的w的最优解 KaTeX parse error: Undefined control sequence: \* at position 3: w^\̲*̲ 满足KKT条件。min-max问题等价于max-min问题

构造并求解约束最优化问题

上式中 $i,j$ 为样本编号， $y_i,y_j$为对应样本的类别标签。取+1或者-1。 $x_i,x_j$为对应样本的特征向量，$(\Phi (x_i)\cdot \Phi (x_j))$表示向量的点乘，通过转置最后点乘结果为一个实数。一个样本对应一个参数 $\alpha$。

将样本点代入到上式中，然后分别对每一个${\alpha }_i$求偏导使其为$0$，并且在上述约束条件下，就能求出每个 ${\alpha }_i$的最优解${\alpha }^{\ast }$。

为什么叫“Support Vector”？

下面的$x$ 可以理解为上面的$\Phi (x)$，只是没有做核函数映射而已。

上面我们已经对w,b求偏导得出：

所以只要求出每个样本对应的${\alpha }_i$，那么最后的支持向量，分割超平面就能确定了，我们上面求w的公式也能看出${\alpha }_i$为零的样本肯定不在支持向量上，因为α=0，那么这个样本点根本没有参与w,b的创建，α！=0的样本点参与了w,b的创建，故α！=0的样本点是支持向量。

求得分离超平面

分类决策函数

线性支持向量机 （软间隔最大化soft margin maximization ）

如何定义软间隔目标函数

• 不一定分类完全正确的超平面就是最好的。（硬间隔SVM可能会过拟合，泛化性能差。）
• 样本数据本身***线性不可分***。

若数据线性不可分，则增加***松弛因子*** ${\epsilon }_i>=0$， 使函数间隔加上松弛变量大于等于1。这样，约束条件变成

目标函数：当然我们也不希望${\epsilon }_i$ 太大，所以在原始的目标函数后加上一项，可以理解成正则项。

在上式中 ${\epsilon }_i$ 的系数$C$ 如果取得非常大，那么即使 ${\epsilon }_i$ 很小乘上$C$ 也是很大。此时目标函数不会是最优，那么就意味着当$C$ 取很大时，只有${\epsilon }_i=0$ 时才能取得最优。即当 $c -> \infty $时，就退化成了线性可分的 SVM。

C其实就是调节对错误的容忍程度，C越大，对错误的容忍度越小，那么过渡带就会越窄。C越小，对错误的容忍度越大，那么过渡带就会越宽。（宽就意味着有泛化能力）

线性SVM的目标函数

带松弛因子的SVM拉格朗日函数

拉格朗日函数：${\epsilon }_i>0$，我们在前面加上负号使其小于0。

对w,b, ξ求偏导得

将三式带入L中，得到：

对上式求关于$\alpha$的极大，得到：

从上面推导出的 $0<=\alpha <=C$，结合之前的讨论当$C$ 很大时，容忍度越低，那么退化为线性可分SVM，因为此时不等式就变成$0<=\alpha$，而在线性可分SVM中的 $\alpha >=0$，正好对应上了。

整理，得到对偶问题：

构造并求解约束最优化问题

求得最优解${\alpha }^{\ast }$

将算出的${\alpha }^{\ast }$代入以下公式：

注意：计算$b$时，需要使用满足条件$0<{\alpha }_j<C$ 的向量，实践中往往取支持向量的所有值取平均，作为b 。

求得分离超平面

分类决策函数

损失函数

在软间隔的SVM上，处于过渡带以内的样本的$\alpha =C$ ，支持向量的 $0<=\alpha <=C$，而在过渡带以外的样本的$\alpha =0$ 。

在过渡带以内的样本是有损失的，虽然过渡带以内的有些样本可能并没有分错。那么这个损失有多大呢？

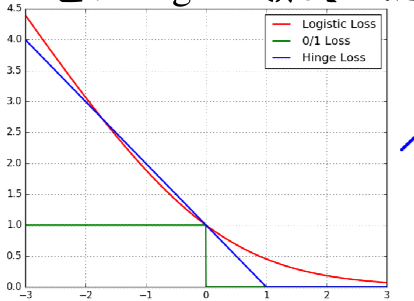
支持向量到分割超平面距离为1，在过渡带以外的样本是没有损失的，在过渡带上的样本（也即是支持向量）损失为0，在过渡带以内的样本的损失就是松弛因子$\epsilon$，这个$\epsilon$可以大于1，因为样本可能会被分错分到分割超平面另一边。那么SVM的损失函数图像即为：

注：横轴表示样本$y_i\cdot (w^T\Phi (x)+b)$值，纵轴表示损失 $\epsilon$，显然当距离大于1是时损失$\epsilon$=0，当距离等于1时$\epsilon$正好为0，当样本距离分割超平面小于1时损失$\epsilon$>0。当样本距离分割超平面距离为0时，也即是正好在分割线上时，损失就为1，所以SVM的损失函数图像过（1,0）和（0,1）点。SVM损失又称hinge损失。

即我们优化的目标是：

我们再回头看上面的目标函数：

这个目标函数的第二项不正是损失函数吗？

所以我们可以将这个目标函数看成这样：

故SVM可以看作hinge损失加上一个L2正则项。

核函数

在上面的线性可分支持向量机和线性支持向量机中，我们是把$\Phi (x)=x$没有做任何高维的映射，所以说是线性的。这里我们开始使用核函数来进行计算分类。

可以使用核函数，将原始输入空间映射到新 的特征空间，从而，使得原本线性不可分的 样本可能在核空间可分。

在实际应用中，往往依赖先验领域知识/交叉 验证等方案才能选择有效的核函数。
没有更多先验信息，则使用高斯核函数。

线性核函数

　　　# 分类器
    ## "ovr"也即是one vs rest，每次选取数据样本中的某一类，剩余的其他类作为一类进行分类
    ## 'ovo'也即是one vs one,每选择其中的两类进行分类
    clf = svm.SVC(C=0.1, kernel='linear', decision_function_shape='ovr')
    # clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')
    clf.fit(x_train, y_train.ravel())

    # 准确率
    print clf.score(x_train, y_train)  # 精度
    print '训练集准确率：', accuracy_score(y_train, clf.predict(x_train))
    print clf.score(x_test, y_test)
    print '测试集准确率：', accuracy_score(y_test, clf.predict(x_test))

    # decision_function
    print 'decision_function:\n', clf.decision_function(x_train)
    print '\npredict:\n', clf.predict(x_train)

多项式核函数

例如：

那么可推得：

这里我们假设X是三维的，那么可得：

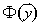
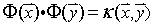
同理可以计算出，那么这里可得。

同理，当多项式核为

那么可得：

若X是三维的可得：

clf=svm.SVC(C=0.1,kernel='poly',degree=3,decision_function_shape='ovr')

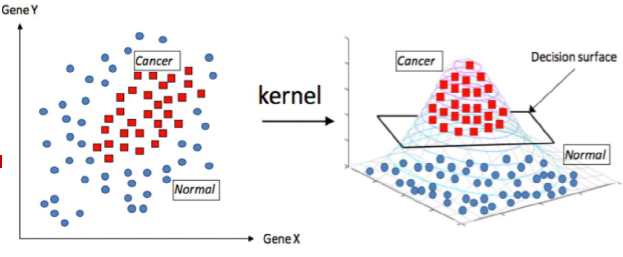
核函数映射图

数据样本在低维不可分，将其映射到高维空间变得可分。

高斯核

高斯核函数里面的参数gamma,gamma越大衰减的越快，离某一个样本最近的样本的相似度都会很低，因此使得分类的精度提高。如果gamma趋近于无穷大，那么就是一个1近邻。经过合适的调参，SVM高斯核函数一定能在训练集上将数据百分百分对。

高斯核是无穷维的
我们利用泰勒展式：

那么可得：

clf = svm.SVC(C=0.8, kernel='rbf', gamma=20, decision_function_shape='ovr')

原始的X是有限维度的，当用高斯核函数映射时，将其映射为n维，也就是无穷维度。

处理不均衡样本问题

设置参数class_weight对少数类的样本赋予较高权重，给予较大的重视。

 # 分类器
    clfs = [svm.SVC(C=1, kernel='linear'),
            ## 参数class_weight用来处理不均衡数据样本
           svm.SVC(C=1, kernel='linear', class_weight={-1: 1, 1: 50}),## 负例给权重1，正例给权重50,以下同理
           svm.SVC(C=0.8, kernel='rbf', gamma=0.5, class_weight={-1: 1, 1: 2}),
           svm.SVC(C=0.8, kernel='rbf', gamma=0.5, class_weight={-1: 1, 1: 10})]